MATLAB强化学习入门——一、多臂赌机问题

零、写在前面

机器学习近几年大火，现在基本上是一个万物均可“机器学习”的状态；本课题组虽然志在航天，亦要紧跟潮流。在机器学习目前较为普及的几大领域，SVM与神经网络模型的主要长处在于图像和语言识别；强化学习则长于处理控制与决策问题。惊艳世人的谷歌AlphaGo等人工智能，简单来说，也是强化学习与深度神经网络的结合。
学习机器学习的缘由也在于此：未来的机器学习模型，可能即如今日的计算机与编程，成为科研、工程中必不可少的工具。于是，决定从强化学习(Reinforcement Learning)入手，理解一些基础的东西。最后的目标呢，则是想实现卫星的强化学习三轴姿态控制。
写这一系列的文章，在于记录自己学习强化学习的过程，并将自己对强化学习体系的理解文字化，丢在这个树洞里。如果有人看并能指点指点，或者从中有所收益，那么也就没白写。

一、何谓“ 强化学习”

强化学习是一种用于求解时序决策问题(sequential decision problem)的机器学习模型。[1] 从强化学习的建模思想上来看，它模仿了人类学习和决策中不断尝试最终得到最优解的过程。在强化学习的过程中，机器不断尝试不同的解决问题的策略，并根据环境的反馈调整策略，最终得到最优的控制策略。具体的来说，强化学习通过将复杂的空间-时序决策问题描述为马尔可夫决策过程(Markov Decision Process)以实现建模与决策。这样，时序决策问题的描述可以划分为智能体(agent)和环境(environment)两大主体，并可由以下的多个要素进行描述：
①智能体A：智能体即强化学习中的控制主体，能够按照某种策略π(policy)，根据当前所处的状态x(state)选择合适的动作a(action)。
②环境E：系统中除智能主体以外的部分，能够根据智能主体的动作向智能主体反馈状态和奖励。其变化一般服从智能主体已知或者未知的某种规律
③状态空间X：智能主体所感知到的每一个对环境的描述，即状态x的整体。例如，在某个离散网格空间中的小球运动问题（如图1所示），小球所处的坐标和移动步数就是一个状态。
④动作空间A：机器在所有状态下所能采取的动作a的整体。例如，离散网格空间中的小球运动问题，小球的向上/向下/向左/向右运动即为一种动作。

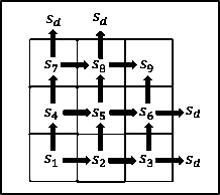
④状态转移概率P：X×A×X→R：描述了了智能主体在现有状态采取某一动作，能够转移到另一状态的概率。
⑤奖励R：X×A×X→R：描述了了智能主体在现有状态采取某一动作转移到另一状态后环境所反馈的奖励。

一般来说，环境可以定义为四元组：E=〈X,A,P,R〉。[2]另外，作为采用策略π选择动作的依据，智能主体往往需要对状态空间中的状态以及状态所对应的动作进行量化估计，这就是状态价值函数 V(x) (state value function)以及状态-动作价值函数 Q(x,a) (state-action value function)。

二、强化学习与控制

作为一种解决时序决策问题的模型，强化学习被Sutton等研究者定义为一种自适应最优控制(adaptive optimal control)方法。[3]他们认为，所有的控制问题都可如下描述：控制某个动力学系统的输入以使其行为满足一系列控制目标。这其中包括两大类问题：①监管和追踪问题(regulation and tracking problem)，②最优控制问题(optimal control problem)。对于第一类问题，控制的任务可以描述为令被控系统的输出与参考轨迹/参考水平相一致。对于第二类问题，则是令受控系统行为所对应的某一类指标最大化。[3]而第二类问题，显然与强化学习的任务内涵相一致。而第一类问题，其本质目标及最小化控制误差，在这一层面上，第一类问题也可采用强化学习方法解决。

强化学习在控制上的常见例子是倒立摆以及小车上山问题。初步的想法是，能不能用强化学习，实现一个卫星的三轴姿态控制，这也就是接下来一系列工作的重心。

三、K-多臂赌机与策略(Policy)

不积硅步，无以至千里。想要入门，最先需要理解的问题就是多臂赌机问题。强化学习问题实际可以将复杂的问题拆分成多步决策问题。而这其中的每一个单步决策问题，对应的就是K-多臂赌机模型(K-armed bandit)。
K-摇臂赌机(K-armed bandit)是强化学习任务中考虑单步奖励最大化时所对应的理论模型。K-摇臂赌机的模型包含K个摇臂，智能主体投入一个硬币后可选择按下其中一个摇臂，每个摇臂以一定的概率吐出硬币（即奖赏），但奖赏以及吐出奖赏的概率智能主体事先并不知道。因此，智能主体的目标即在于通过一定的策略最大化所能获得的奖赏，即获得最多的硬币。

3.1 “探索”与“利用”的矛盾

由于智能主体事先并不知道各摇臂的回报及其概率，因此，想要最大化总体汇报，就必须通过一定的方法估计各摇臂回报的数学概率，这也就是强化学习的“探索”方法(exploration)。而一旦完成了对各摇臂回报情况的估计，那么就应当根据这种估计选择预期能够获得最大回报的摇臂；这也就是“利用”方法(exploitation)。
在一个多臂赌机问题的循环中，显然需要即使用“探索”方法，也使用“利用”方法，以实现最大化总体奖赏的目标。如果“探索”次数过少，则可能对各摇臂的数学期望估计不准确。如果“利用”次数过少，则不能很好的利用估计得到的期望最大化奖赏。这就是“探索”与“利用”之间的矛盾。
针对上述矛盾，几种基本的策略被提出，包括ε-greedy策略、softmax策略、时变ε-greedy策略。

3.2 ε-greedy策略

ε-greedy策略基于一个概率来对探索和利用进行折中：每次尝试时，以ε的概率进行探索，以1-ε的概率进行利用。进行探索时，以均匀概率随机选取摇臂；进行利用时，则选择当前平均奖赏最高的摇臂。
这里考虑一个k=5的多臂赌机，其各摇臂的对应反馈均为二值的，即以P的概率返回奖赏，以1-P的概率返回另一值。下表展示了摇臂的奖赏及其概率。

序号	概率P	反馈1	反馈2
1	0.2	1	0
2	0.1	2	0
3	0.3	1	-1
4	0.5	2	-1
5	0.4	2	0

从数学期望上讲，摇臂5具有最大的回报期望，无论怎样选择摇臂，随着尝试次数增多，最后得到的平均回报都不会超过这一期望。这样因此，一个理想的策略应该在尝试足够多次数后令所获得的平均回报不断接近这一值。

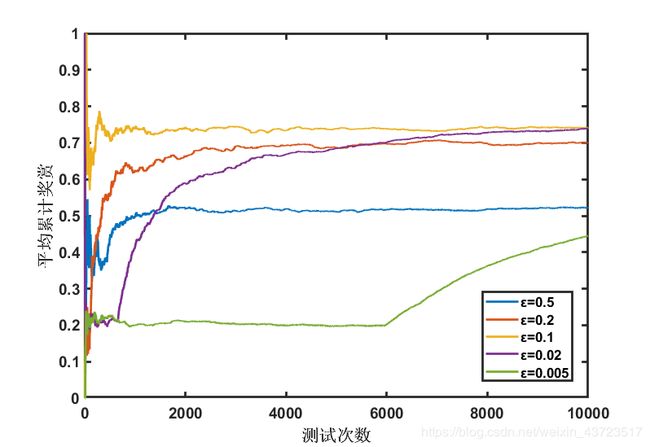
图2 ε-greedy策略所获得的平均回报

采用ε-greedy策略选择摇臂，ε取不同的值，得到的回报情况如上。当ε较大时（如ε=0.5），得到的回报显然是不理想的，原因在于即是已经获得了对多臂赌机的准确估计，智能体仍然浪费机会进行不必要的探索，降低了总体回报。当ε过小（如ε=0.05）时，显然由于探索次数过小，智能体迟迟不能准确的估计得到最佳选项，因此，明显的回报上升直到6000次以后才出现。

3.2.1 代码实现

具体的代码实现上，使用MATLAB语言。由于强化学习的本意在于智能体通过学习对环境建模，因此，需要将智能体部分代码与摇臂赌机（即环境）分别封装，即将摇臂赌机作为函数封装，这样对于智能体，摇臂赌机将是一个给输入只得到输出的"黑箱"。

%I thought what I'd do was I'd pretend I was one of those deaf-mutes，or should I ?

clear all;
epsilon=[0.5,0.2,0.1,0.02,0.005];  %epsilon概率进行探索（exploration），1-epsilon概率进行利用(exploitation)
m=5;

T=10000;
%决策机内存初始化
Avegain=zeros(m,5);  %
Testtime=zeros(m,5);
Reward=zeros(5,T);

for k=1:m
    for i=1:T
        if rand(1)<=epsilon(k) %探索
            num=unidrnd(5);  %随机生成最大为5的正整数，随机选择摇臂
        else   %利用
            a=findmax(Avegain(k,:));
            num=a(2);%选择平均奖赏最大的摇臂
        end
        r=Slotmachine5(num);
        if i==1                                            %更新累计奖赏
            Reward(k,i)=r;
        else
            Reward(k,i)=(Reward(k,i-1)*(i-1)+r)/i;
        end        
        Avegain(k,num)=(Avegain(k,num)*Testtime(k,num)+r)/(Testtime(k,num)+1); %更新所选臂的平均奖赏
        Testtime(k,num)=Testtime(k,num)+1;                 %更新所选臂的实验次数
    end
end
result.Testtime=Testtime;
result.Avegain=Avegain;
result.Reward=Reward;
plot(1:10000,Reward);
xlabel('测试次数');
ylabel('平均累计奖赏');
legend('ε=0.5','ε=0.2','ε=0.1','ε=0.02','ε=0.005');

代码最后的result结构主要用于保留结果，而随后讨论的softmax算法及时变ε-greedy算法均采用类似方法实现。完整的代码将作为资源上传。

3.3 softmax策略

softmax是另一种用于平衡探索和利用的算法。在这种方法中，智能体依据某种概率分布选择摇臂，而概率分布则是基于当前平均奖赏的Boltzmann分布：

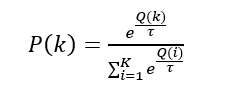
其中，τ>0是用于调节选择情况的参数。τ越小时平均奖赏越高的摇臂被选择的概率越高。因此，τ趋近于0时，智能体趋于“仅探索”。

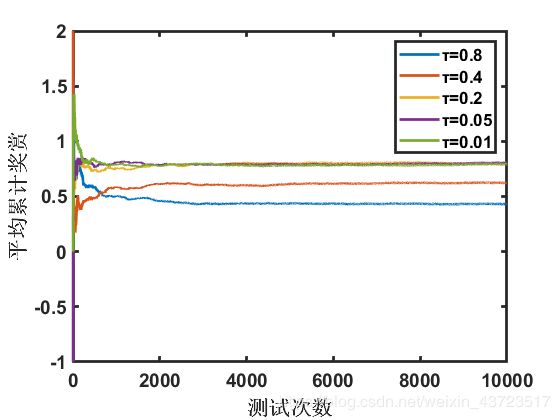
图3 soft策略所获得的平均回报

softmax策略得到的回报情况如图3所示，显然该策略相比ε-greedy能更快的到达稳态状态。但该方法对环境的估计和选择随机性较高。图四则展示了相同赌机、相同策略模拟下的另一组解。

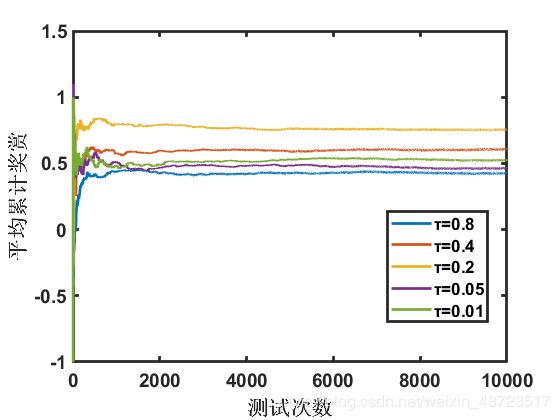
图4 softmax所获得的平均回报II

相同的τ值在初始尝试结果情况不同的情况下，显然不能得到相同的平均回报。而从长期平均回报来看，该策略也略逊于ε-greedy策略。

3.4 时变ε-greedy策略

有没有一种方法，能在初期尽可能多的进行“探索”，以求准确估计，而在后期尽可能多的“利用”，以求最大化平均回报？
时变ε-greedy提供了解决方案，将ε定义为随时间减小的函数，从而实现上述设想。例如定义ε=1/√t，其结果如图5。

图5 时变ε-greedy所获得的平均回报

四、总结

这一篇文章将是强化学习之路的开头。在啰嗦了定义和理解之后，讨论了几种单步决策使用的策略及其特点。解决了单步决策策略问题，就可以考虑多步决策问题，这就是网格迷宫模型。之后也会采用类似的形式分享自己的想法。具体的代码将会以代码包的形式上传至资源里。

[1] Xin Xu, Lei Zuo, Zhenhua Huang. Reinforcement learning algorithms with function approximation: Recent advances and applications[J]. Information Sciences,2014,261.
[2] 周志华. 机器学习[M]. 北京：清华大学出版社, 2016.
[3] Sutton, Richard S., Barto, Andrew G., Williams, Ronald J… Reinforcement Learning is Direct Adaptive Optimal Control[P]. American Control Conference, 1991,1991.