编译原理 - 语法分析(自上而下)
语法分析
- 编译 :高级语言->汇编语言( .s)
- 语法分析
- 任务 : 识别是否为句子
- 语法分析器 : 是否符合文法规则
- 语法分析的分类
- 自上而下 ⭐
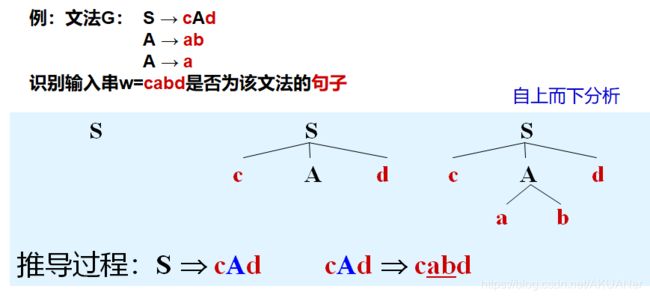
- 自上而下的主旨 - 最左推导
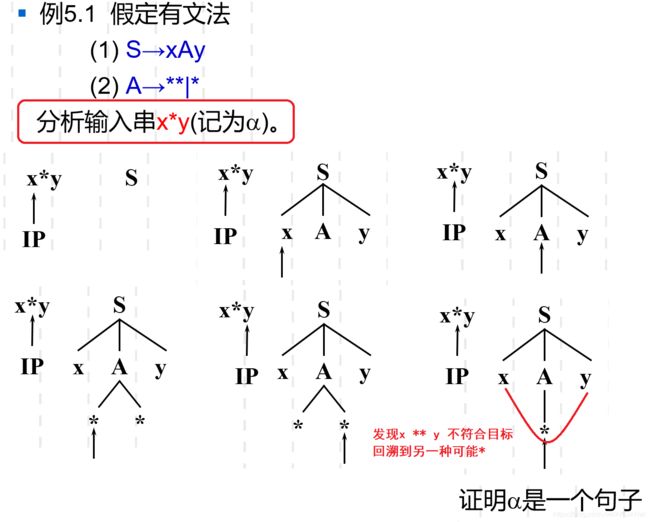
- 自上而下 存在问题 - 上下文无关文法
- 存在回溯问题 - 效率低
- 左递归问题 - 陷入了无限循环
- 常见左递归形式
- 左递归的消除 - LL(1)分析法
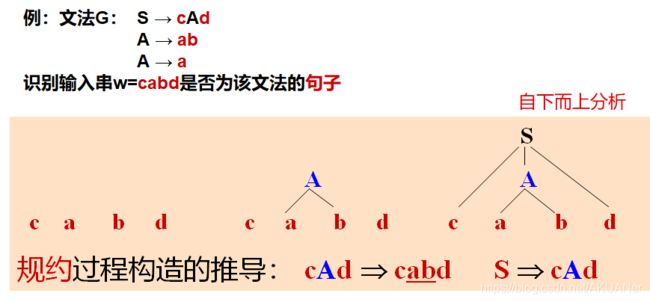
- 自下而上
- 左递归的消除:
- 直接左递归消除 - 左递归改右递归
- 通式推导:
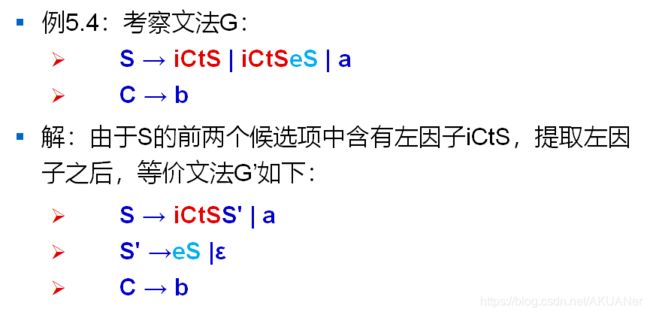
- 经典案例:⭐
- 举例说明2
- 间接左递归的消去 - 代入法
- 代入法步骤
- 通式推导
- 举例说明⭐
- 举例说明2 - 代入顺序的不同不影响文法的等价性
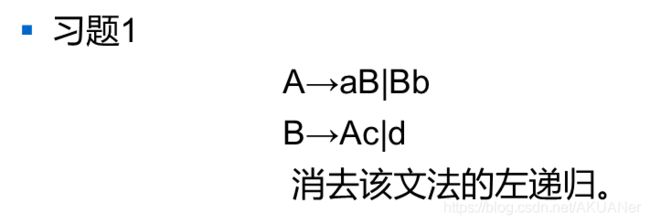
- 作业例题
- 注意事项
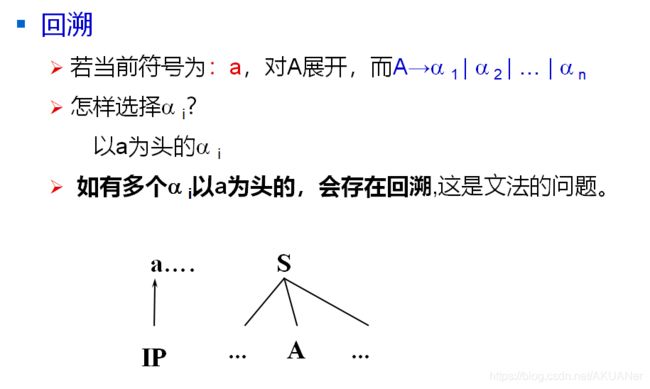
- 回溯的消除
- 回溯的产生
- 回溯的消除
- 终结首符集FIRST(α) - 匹配a时候找到了对应候选式
- 消除回溯的方法 - 提取公共左因子 - 使得候选尽可能不相交
- 消除回溯例题 - 提取公共左因子
- FOLLOW集合 - 当匹配的a不属于FIRST(α)时 (没找到对应候选式)
- 构造LL(1) 文法 :构造不带回溯的自上而下分析的文法
- 什么是LL(1)文法
- 构造LL(1)文法的条件
- LL(1)分析步骤
- 构建FIRST集合和FOLLOW集合
- 构建FIRST集 ⭐
- 单个文法符号的FIRST集 - α串由单字符X组成
- 一组文法符号串的FIRST集 - α串由n个Xi字符组成
- 构造FOLLOW集
- FOLLOE集合例题
- LL(1) 方法
- LL(1)具体实现 - 构造递归下降分析器
- 当前程序没有递归机制 - LL预测分析
- 预测分析器模型
- 预测分析流程
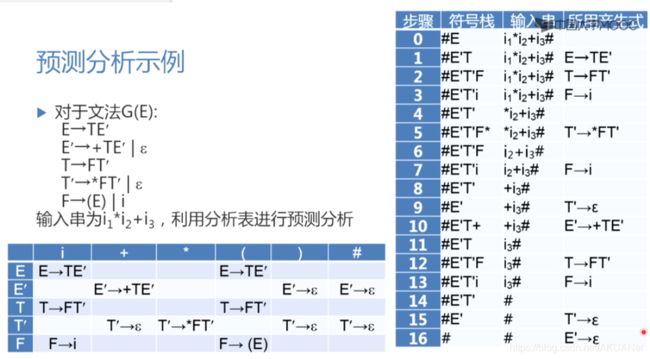
- 预测分析举例
- 预测分析表 - 矩阵(二维数组)
- 构造预测分析表
- 预测分析器
编译 :高级语言->汇编语言( .s)
1.词法分析 :单词组成是否合乎规则
2.语法分析 :每一行表达式是否正确
3.语义分析 :结合上下文分析是否正确
4.代码优化
5.生成汇编指令 (低级语言)
语法分析
任务 : 识别是否为句子
语法分析器 : 是否符合文法规则
语法分析的分类
自上而下 ⭐
自上而下的主旨 - 最左推导
自上而下 存在问题 - 上下文无关文法
存在回溯问题 - 效率低
左递归问题 - 陷入了无限循环
最左推导的时候陷入了无限循环,递归
区别概念:
=> 推导 , ->定义
常见左递归形式
左递归的消除 - LL(1)分析法
改写文法,致使不含有左递归
自下而上
左递归的消除:
改写文法消除左递归
直接左递归消除 - 左递归改右递归
直接左递归常见形式 : P -> PXXXXX
用p’代替α…α
通式推导:
经典案例:⭐
举例说明2
间接左递归的消去 - 代入法
代入法步骤
通式推导
循环n次,每循环执行一次,就对该当前情况直接左递归的判断和消除
直到循环结束,把所有的直接左递归给消除

举例说明⭐
<-仔细观察代入的过程 , 里面包含了运算和化简->
一步一步代入判断 :
有直接左递归 : 消除
没有 : 继续代入
end ,全代入完毕

举例说明2 - 代入顺序的不同不影响文法的等价性
作业例题
注意事项
代入的目的: 产生直接左递归
∴ 如果产生不了S->SXX形式,就不用代入了

回溯的消除
回溯的产生
回溯的消除
保证在文法中
A -> α1|α2|α3…αn
对A展开时候,有n 个选项, 选择正确的那一项,A多次展开,每次都选择正确的那一项,就不会存在回溯


终结首符集FIRST(α) - 匹配a时候找到了对应候选式
IP所指向是正在匹配的单词,我需要匹配a
那么我A展开的时候 如果是终结符号,就匹配a即可
如果全是非终结符号,那么我就找那个 经过若干展开后可以匹配出a开头的串就行了鸭
引入FIEST集合
 一个串α,能推出a或者a开头的串,那么这个α 就属于FISET(α)
一个串α,能推出a或者a开头的串,那么这个α 就属于FISET(α)
特例: 推出ε,也算α属于FIRST(α)
VT : 终结符号集合

 目的:
目的:
两个FIRST(α),FIRST(α2)元素不想交,所以选择的时候,不是前者就是后者,不会出现重叠的情况,通过这样 找到唯一一个正确的候选去展开


消除回溯的方法 - 提取公共左因子 - 使得候选尽可能不相交
消除回溯例题 - 提取公共左因子
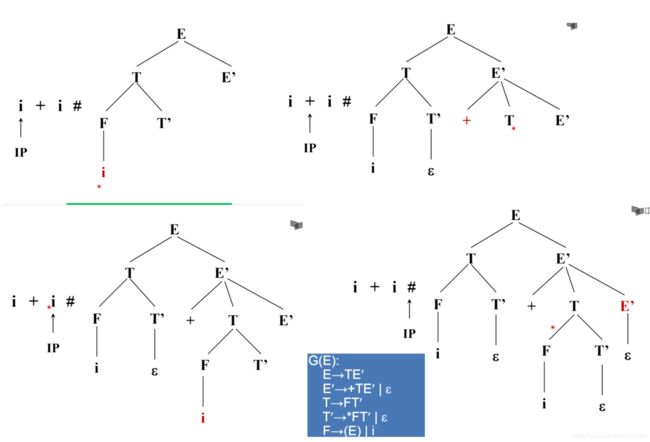
FOLLOW集合 - 当匹配的a不属于FIRST(α)时 (没找到对应候选式)
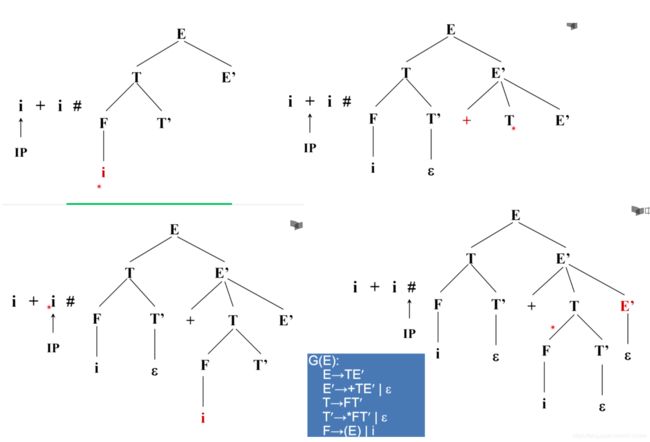 构建成功,是因为存在E => IT’+TE’
构建成功,是因为存在E => IT’+TE’
T’=> 空
 定义: FOLLOW(A) = {a|S=>Aaaa.aa} 能跟在A后面的非终结符号(多指ε),都在FOLLOW集合里面
定义: FOLLOW(A) = {a|S=>Aaaa.aa} 能跟在A后面的非终结符号(多指ε),都在FOLLOW集合里面
使用:如果当A扩展的时候,假设匹配a的时候,a没有出现在任何候选里面(也扩展不出a)时候,如果a在FOLLOW集合里面,把A替换成ε
特殊情况: S=>…A,以A结尾 那么#也属于FOLLOW集合


构造LL(1) 文法 :构造不带回溯的自上而下分析的文法
什么是LL(1)文法
L:从左往右扫描
L:最左推导
1:每一步只需向前查看1个符号
构造LL(1)文法的条件
没有左递归, 候选式不相交,候选是α中不存在空(ε)和包含空(ε)的元素


LL(1)分析步骤
构建FIRST集合和FOLLOW集合
构建FIRST集 ⭐
单个文法符号的FIRST集 - α串由单字符X组成
X=a a在FIEST(X)集合中
X -> b b在FIRST(X)集合中,X -> ε,ε在FIRST(X)中
X -> Y ,Y-> c… , c在FIRST(Y)中 .在FIRST(X)中 – 所有FIRST(Y)中元素(除了ε)都在FIRST(X)中
X -> Y0 ,Y0->Y1Y2Y3…Yn ,把每个Yi对应的非ε都加入FIRST(X)中
若Y1…Yn 每个Yi都有ε,把ε加入FIRST(X)中
Y…Yn 是非终结 - 大写字母
对于 X -> ... 这条产生式而言,
【1】若右边第一个符号是终结符或 ε ,则直接将其加入 First(X)
【2】若右边第一个符号是非终结符,则将其 First 集的的非 ε 元素加入 First(X)
【3】若右边第一个符号是非终结符而且紧随其后的是很多个非终结符,这个时候就要注意是否有 ε 。
【3.1】若第 i 个非终结符的 First 集有 ε ,则可将第 i+1 个非终结符去除 ε 的 First 集加入 First(X)。
【3.2】若所有的非终结符都能够推导出 ε ,则将 ε 也加入到 First(X)
E.G. G[S]:
S -> ABCD
A -> a | ε
B -> b | ε
C -> c
D -> d
解:
First(S) = {a, b, c},其中 c 是由上面所说的第二、三条规则所推得出来的,因为此时 A 和 B 都可以等于空串( ε ),所以非终结符 C 的 first 集合就被加入 G[S] 了。
如果这里 C,D 也能够产生 ε 的话,根据第三条规则中的第二小点,此时 First(S) = {a, b, c, d, ε}
一组文法符号串的FIRST集 - α串由n个Xi字符组成
{ε} : 去掉ε
把首元素的FIRST(X1)集合,去掉ε ,其余剩下元素加到FIRST(α)中,同理遍历整个串α
只有α = X1X2…Xn ,X1~Xn所有FIRST(Xi)中都有ε时候,最后才把ε加入到FIRST(α)中





构造FOLLOW集
参考博客:https://www.cnblogs.com/Bw98blogs/
【1】将所有产生式的候选式(即产生式右部)的非终结符都找到,定位到你想要求解 Follow 集的非终结符的位置,从当前位置往后挨个检查。设 A -> aBC 是一个产生式,在这个产生式中, B 和 C 是非终结符,a 是终结符
【2】先检验这个非终结符的右边还有没有别的符号(终结符或非终结符都可以),在例子中 B 是需要检查的第一个非终结符,它的右边是有非终结符 C 的。
【2.1】若右边有符号 -> 将 First(右侧第一个符号)的非 ε 集合加入到 Follow(当前符号)中,如果 First(右侧第一个符号)含有 ε ,即有 ... -> ε ,则将 Follow(产生式左部符号)加入 Follow(当前符号)中。
E.G. 用 A -> aBC 来说就是,当前扫描到 B 了,而 B 的右侧有非终结符 C,则将去掉 ε 的 First(C)加入 Follow(B)中。若存在 C -> ε ,则将 Follow(A)也加入 Follow(B)中。
【2.2】若右边没有符号了,例如这里的 C,那么可以将 Follow(A)中的元素全部加入到 Follow(C)中。
【3】判断当前符号是不是文法的开始符号,比如 G[A] 中的非终结符 A 就是 G[A] 文法的开始符号,如果是的话就将“#”也加入到 Follow(当前符号)中去。
FOLLOE集合例题
LL(1) 方法
LL(1)具体实现 - 构造递归下降分析器
 ADVANCE : 读入单词符号
ADVANCE : 读入单词符号
SYM: 当前所指的输入符号
以A为例: 写出A的递归下降子程序PROCEDURE A
如果匹配ε,则是看当前单词是否在FOLLOW(A)里面
如果匹配ε,什么都不做
T: 匹配T
E:匹配E’

ADVANCE :继续读入下一单词
先看只有1个非终结符的F->
E : 和E进行匹配
如果匹配ε,则是看当前单词是否在FOLLOW(A)里面
如果匹配ε,什么都不做
 假设经过之前计算得到FOLLOW(W) = { ) , # }
假设经过之前计算得到FOLLOW(W) = { ) , # }
这两个PROCEDURE E’等价
SYM<>’#’ AND SYM<>’)’
本质就是查看当前单词有没有在FOLLOW(E)里面

 写出各个 非终结符程序后, 需要写出一个主程序
写出各个 非终结符程序后, 需要写出一个主程序
负责调用词法分析程序ADVANCE读入第一个单词
当前程序没有递归机制 - LL预测分析
预测分析器模型
预测分析程序 : 自上而下语法分析
a + b # :输入串
根据分析表,选择合适的候选式(展开)进行匹配


预测分析流程
预测分析举例
i1i2i3 都是i 只不过用下标区分顺序而已
栈顶 是 非终结符,弹出非终结符,压入展开的产生式
预测分析表 - 矩阵(二维数组)
构造预测分析表
A->α 应该放到A那一行,FIRST(α)列
A->ε,应该放到A那一行,FOLLOW(A)内所有列