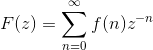matlab符号及其运算（2）

1.嵌套符号表达式

horner函数实现对符号表达式进行嵌套

• R = horner(P)：P为待嵌套的符号表达式，R为嵌套后的符号表达式

>> syms x y
>> horner(x^3 - 6*x^2 + 11*x - 6)
 
ans =
 
x*(x*(x - 6) + 11) - 6
 
>> horner([x^2 + x;y^3 - 2*y])
 
ans =
 
   x*(x + 1)
 y*(y^2 - 2)

2.分解符号表达式

factor函数用于实现符号表达式的分解

• factor(X)：X为多项式或多项式矩阵，系数是有理数，X最后表示成有理数低阶多项式相乘的形式，如果不能有理数范围内因式分解，则会返回X本身。

>> syms x y
>> factor(x^3 - y^3)
 
ans =
 
(x - y)*(x^2 + x*y + y^2)
 
>> factor(sym('12345678901234567890'))
 
ans =
 
2*3^2*5*101*3541*3607*3803*27961

3.化简符号表达式

根据一定的规则对符号表达式进行化简，函数为simplify

• simplify(S)：输入参数S为符号表达式或符号矩阵
• simplify(S,Name,Value)：指定一个符号表达式的属性名及对应的属性值，并对矩阵或表达式进行化简

>> % 对符号表达式进行化简
>> syms x a b c
>> simplify(sin(x)^2 + cos(x)^2)
 
ans =
 
1
 
>> % 对符号矩阵进行化简
>> simplify([(x^2 + 5*x + 6)/(x + 2),sin(x)*sin(2*x) + cos(x) * cos(2*x);(exp(-x*i)*i)/2 - (exp(x*i)*i)/2,sqrt(16)])
 
ans =
 
[  x + 3, cos(x)]
[ sin(x),      4]
 
>> % 使用IgnoreAnalyticConstraints规则对符号表达式进行化简
>> s = (log(x^2 + 2*x + 1) - log(x + 1)) * sqrt(x^2);
>> simplify(s)
 
ans =
 
-(log(x + 1) - log((x + 1)^2))*(x^2)^(1/2)

4.替换符号表达式

当表达式结构复杂、变量较多的时候，引入一些新的变量进行代换，变化结果，从而达到解决问题的目的，这种方法称为变量代换法。matlab提供了subs函数和subexpr函数进行变量代换或者叫做符号表达式的替换。

subs函数利用符号变量或符号表达式替换目标符号表达式中的符号变量

subexpr函数利用符号变量替换目标符号表达式的某个子符号表达式

subs函数：

subs函数可以用指定符合替换符号表达式中的某一特定符号

• R = subs(S)：用函数中的值或matlab工作区间的值替代符号表达式S中的所有变量，如果没有指定符号变量的值，则返回值中的该符号变量不被替换
• R = subs(S,new)：用新的符号变量new代替原来的符号表达式S中的默认变量
• R = subs(S,old,new)：用新的符号变量new替换原来符号表达式S中的变量old，当new是数值形式的符号时，实际上用数值替换原来的符号计算表达式的值，结果仍为字符串形式

>> syms a b
>> subs(a + b, a, 4)
 
ans =
 
b + 4

>> syms a b;
>> subs(cos(a) + sin(b),{a, b}, {sym('alpha'), 2})
 
ans =
 
sin(2) + cos(alpha)

subexpr函数：

subexpr函数将表达式中重复出现的字符串用变量代换。

• [Y,SIGMA] = subexpr(X, SIGMA)：指定用变量SIGMA的值，来代替符号表达式中重复出现的字符串。进行替换后，函数的返回值Y，被替换的符号变量由SIGMA返回
• [Y,SIGMA] = subexpr(X,'SIGMA')：函数中输入参数SIGMA为字符或字符串，用来替换符号表达式中重复出现的字符串。进行符号替换返回值为Y，被替换的符号变量由SIGMA返回 

>> syms a b c d x
>> solutions = solve(a * x ^ 3 + b * x ^ 2 + c * x + d == 0,...
x,'MaxDegree',3);
>> [r,sigma] = subexpr(solutions)
 
r =
 
                                                                             sigma^(1/3) - b/(3*a) - (- b^2/(9*a^2) + c/(3*a))/sigma^(1/3)
 (- b^2/(9*a^2) + c/(3*a))/(2*sigma^(1/3)) - sigma^(1/3)/2 + (3^(1/2)*(sigma^(1/3) + (- b^2/(9*a^2) + c/(3*a))/sigma^(1/3))*i)/2 - b/(3*a)
 (- b^2/(9*a^2) + c/(3*a))/(2*sigma^(1/3)) - sigma^(1/3)/2 - (3^(1/2)*(sigma^(1/3) + (- b^2/(9*a^2) + c/(3*a))/sigma^(1/3))*i)/2 - b/(3*a)
 
 
sigma =
 
((d/(2*a) + b^3/(27*a^3) - (b*c)/(6*a^2))^2 + (- b^2/(9*a^2) + c/(3*a))^3)^(1/2) - b^3/(27*a^3) - d/(2*a) + (b*c)/(6*a^2)
 

5.符号函数的操作

matlab提供了把两个符号函数符合成一个符号函数的功能函数，同时也提供了对符号函数表达式的逆功能函数

compose函数：函数表达式的符合运算

• compose(f,g)：返回函数当f=f(x)和g=g(y)时的符合函数f(g(y)).x为由函数findsym确定的f的符号变量，y有函数findsym确定的g的符号变量
• compose(f,g,z)：返回f = f(x) 和 g = g(y) 时的符号函数f(g(z))，返回的函数以z为自变量。
• compose(f,g,x,z)：返回符合函数f(g(z)),x为函数f的独立变量。
• compose(f,g,x,y,z)：返回复合函数f(g(z)),并且x为函数f的独立变量，y为函数g的独立变量

>> syms x y z t u
>> f = 1/(1 + x^2);
>> g = sin(y);
>> h = x^t;
>> p = exp(-y/u);
>> a = compose(f,g)
 
a =
 
1/(sin(y)^2 + 1)
 
>> c = compose(h,g,x,z)
 
c =
 
sin(z)^t

finverse函数：实现符号表达式的反函数操作

• g = finverse(f)：计算输入参数的反函数，f为符号表达式，返回值g也是一个符号表达式
• g = finverse(f,var)：输入参数var为一个符号变量，是函数f中的变量，且该函数的返回值g是var为自变量。

 

>> syms t x
>> f1 = finverse(log(t))
 
f1 =
 
exp(t)
 
>> f2 = finverse(cos(2 * t) + 1)
 
f2 =
 
acos(t - 1)/2

6.符号微积分

符号表达式的极限：

求微分的基本思想是当自变量趋近某个值时，求函数值的变化。“无穷逼近”是为基本的一个基本思想。

matlab中用limit函数求表达式的极限

• limit(expr, x, a)：求符号函数expr(x)的极限值。即计算当变量x趋近于常量a时，expr(x)的极限值
• limit(expr,a)：求符号函数expr(x)的极限值。变量为函数findsym(expr)确定的默认变量
• limit(expr)：求符号函数expr(x)的极限值。默认趋近于0
• limit(expr, x, a, 'left')：求符号函数expr的极限值。left表示变量x从左边趋近于a，换成‘right'，就是从右边趋近去a

>> syms x;
>> f1 = sym((cos(x) + sin(x) - x)/x)
 
f1 =
 
(cos(x) - x + sin(x))/x
 
>> limit(f1,x,inf)
 
ans =
 
-1
 
>> limit(f1,x,0)
 
ans =
 
NaN

符号表达式的微分：

diff可以完成一元或多元函数的任意阶数的微分，对于自变量的个数多余一个的符号矩阵，微分为Jocabian矩阵，采用jacobian函数实现微分

(1) diff函数

• diff(expr)：没有指定变量和导数阶数，则系统按findsym函数指示的默认变量对符号表达式expr求一阶导数
• diff(expr,v)：指定符号表达式的变量v
• diff(expr,sym('v'))：计算符号表达式expr的一阶导数，以符号变量v为自变量
• diff(expr,n)：对符号表达式expr求n阶导数
• diff(expr,v,n)：计算符号表达式expr的n阶导数，以符号变量v为自变量

>> syms x
>> f = exp(-2*x) * cos(2*x^0.5)
 
f =
 
exp(-2*x)*cos(2*x^(1/2))
 
>> g = diff(f,4)
 
g =
 
16*exp(-2*x)*cos(2*x^(1/2)) - (24*exp(-2*x)*cos(2*x^(1/2)))/x - (11*exp(-2*x)*cos(2*x^(1/2)))/x^2 - (15*exp(-2*x)*cos(2*x^(1/2)))/(4*x^3) + (32*exp(-2*x)*sin(2*x^(1/2)))/x^(1/2) + (4*exp(-2*x)*sin(2*x^(1/2)))/x^(3/2) + (3*exp(-2*x)*sin(2*x^(1/2)))/x^(5/2) + (15*exp(-2*x)*sin(2*x^(1/2)))/(8*x^(7/2))
 
>> pretty(g)
                  exp(-2 x) #2 24   exp(-2 x) #2 11
exp(-2 x) #2 16 - --------------- - ---------------
                         x                  2
                                           x

     exp(-2 x) #2 15   exp(-2 x) #1 32   exp(-2 x) #1 4
   - --------------- + --------------- + --------------
              3            sqrt(x)             3/2
           4 x                                x

     exp(-2 x) #1 3   exp(-2 x) #1 15
   + -------------- + ---------------
           5/2                7/2
          x                8 x

where

   #1 == sin(2 sqrt(x))

   #2 == cos(2 sqrt(x))

(2) jacobian函数

matlab中,提供了jacobian函数用于求多元函数的导数。

• jacobian(f,v)：计算数量或向量f对于向量v的jacobian矩阵。函数的返回值第i行第j列的数位df(i)/dv(j).当f为数量时，该函数返回f的梯度。参数v可以是数量，jacobian(f,v)等价于diff(f,v).

>> syms x y z
>> f = [x*y*z; y; x+z];
>> v = [x, y, z];
>> R = jacobian(f,v)
 
R =
 
[ y*z, x*z, x*y]
[   0,   1,   0]
[   1,   0,   1]
 
>> b = jacobian(x+z,v)
 
b =
 
[ 1, 0, 1]

符号表达式的积分:

int函数求符号表达式的积分

• int(f)：没有指定变量和阶数，按默认的变量求不定积分
• int(f,v)：以v为自变量，对被积分函数或符号表达式f求不定积分
• int(f,a,b)：符号表达式采用默认变量，该函数求默认变量从a到b时符号表达式f的定积分数值，如果f为符号矩阵，则积分对各个元素分别进行积分
• int(f,v,a,b)：求变量v在区间a到b之间的定积分

>> syms a x t z
>> int(-2 * x/(1 + x^2)^2)
 
ans =
 
1/(x^2 + 1)
 
>> int(x/(1 + z^2), x)
 
ans =
 
x^2/(2*(z^2 + 1))

级数求和：

在matlab中提供了symsum函数用于求符号表达式的和。其调用格式为：

• F = symsum(f,k,a,b)：求符号表达式f中变量k从a到b时的有限和
• F = symsum(f,k)：计算符号表达式f中指定变量为k的有限项和

>> syms k x
>> S1 = symsum(k^2,k,0,10)
 
S1 =
 
385
 
>> S2 = symsum(1/k^2,k,1,Inf)
 
S2 =
 
pi^2/6

泰勒级数：

taylor函数用于求符号表达式的泰勒级数展开式

• taylor(f,var)：指定符号变量为var，求Maclaurin多项式
• taylor(f,var,a)：返回符号多项式f中的指定符号自变量var的n-1阶的Maclaurin多项式近似式，其中var可以是字符串或符号变量
• taylor(_,Name,Value)：指定一个或多个属性名及其属性值，实现对符号表达式进行泰勒级数

>> syms x
>> tayor(exp(x))
>> taylor(exp(x))
 
ans =
 
x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1
 
>> taylor(sin(x))
 
ans =
 
x^5/120 - x^3/6 + x

7.符号积分变换

傅里叶变换及其反变换：

• Fw = fourier(f, t, w)：求时域上函数f的傅里叶变换Fw
• f = ifourier(Fw,w,t)：求频域上函数Fw的傅里叶反变换f

>> syms w x y z a b c d t
>> f = exp(-x^2);
>> fourier(f,x,y)
 
ans =
 
pi^(1/2)*exp(-y^2/4)
 
>> F = sqrt(sym(pi)) * exp(-y^2/4);
>> ifourier(F,y,z)
 
ans =
 
exp(-z^2)

拉普拉斯变换及其反变换：

• Fs = laplace(f,trans_var,eval_point)：求时域上函数f的拉普拉斯变换Fs
• f = ilaplace(Fs,trains_var,eval_point)：求频域上函数f的拉普拉斯反变换f

>> syms a b c d w x y z t s
>> f = 1/sqrt(x);
>> laplace(f,x,y)
 
ans =
 
pi^(1/2)/y^(1/2)
 
>> F = 1/y^2;
>> ilaplace(F,y,x)
 
ans =
 
x
 

z变换及其反变换：

• Fz = ztrans(f, trans_index,eval_point)：求时域函数f的Z变换Fz
• f = iztrans(Fz, trans_index,eval_point)：求频域函数Fz的Z逆变换f

>> syms a b c d w x y z k t n
>> f = sin(k);
>> ztrans(f, k, x)
 
ans =
 
(x*sin(1))/(x^2 - 2*cos(1)*x + 1)
 
>> F = 2*x/(x-2)^2;
>> iztrans(F,x,k)
 
ans =
 
2^k + 2^k*(k - 1)