形态学及边缘角点检测

形态学滤波理论于上世纪90年代提出，目前被广泛用于分析及处理离散图像。其基本运算有4个： 膨胀、腐蚀、开启和闭合， 它们在二值图像和灰度图像中各有特点。基于这些基本运算还可推导和组合成各种数学形态学实用算法，用它们可以进行图像形状和结构的分析及处理，包括图像分割、特征抽取、边缘检测、 图像滤波、图像增强和恢复等。数学形态学方法利用一个称作结构元素的“探针”收集图像的信息，当探针在图像中不断移动时， 便可考察图像各个部分之间的相互关系，从而了解图像的结构特征。数学形态学基于探测的思想，与人的FOA(Focus Of Attention)的视觉特点有类似之处。其中最重要的结构元素，可直接携带知识（形态、大小、甚至加入灰度和色度信息）来探测、研究图像的结构特点。鉴于研究所需，记录一些知识点，开发平台为OpenCV2.4.9+Qt5.3.2。

一：图像腐蚀、膨胀和开闭运算

这些运算的基本公式和原理参考：http://blog.csdn.net/liyuefeilong/article/details/43374777 
图像的腐蚀：替换为当前像素位像素集合中的最小像素值，函数为cv::erode 
图像的膨胀：替换为当前像素位像素集合中的最大像素值，函数为cv::dilate 
图像的开运算：先腐蚀后膨胀，函数为cv::morphologyEx，对应的参数为MORPH_CLOSE 
图像的闭运算：先膨胀后腐蚀，函数为cv::morphologyEx，对应的参数为MORPH_OPEN 

如morphologyEx(image, opened, cv::MORPH_OPEN, element2, cv::Point(-1,-1), 1); 中，输入图像为image，输出图像为opened，执行开操作，结构元素为element2，原点参数cv::Point(-1,-1)表示原点位于矩阵的中心（默认）,最后的1则表示对图像的操作次数（注：对一幅图像多次使用开操作和闭操作时效果不会有改善，这些运算是等幂的）。形态学滤波本是基于二值图像上，但以上这些运算同样适用于灰度图像。

高斯差分技术：

 

1、用 相同尺寸，不同标准差 的两个高斯核去卷积图像。

2、计算两幅卷积结果的差。

3、将差归一到 0-255，形成差分图像。

 

但从 DOG 的公式看，是可以先计算高斯核的差，生成高斯差分核，再去卷积图像。这样做的好处是只卷积一次图像。

经验证这是可行的，需要注意的几点是：

1、计算高斯核的差时要先除以各自的系数和。

2、如果考虑边界，那么高斯差分核就不止一个。比如 3×3 的高斯核，就需要3个高斯差分核，一个处理4个顶点，一个处理4条边（除顶点），一个处理中间部分。因为它们各自要除以的系数和不同。

Canny边缘检测器：

 Canny边缘检测算法的处理流程

Canny边缘检测算法可以分为以下5个步骤：

1)        使用高斯滤波器，以平滑图像，滤除噪声。

2)        计算图像中每个像素点的梯度强度和方向。

3)        应用非极大值（Non-Maximum Suppression）抑制，以消除边缘检测带来的杂散响应。

4)        应用双阈值（Double-Threshold）检测来确定真实的和潜在的边缘。

5)        通过抑制孤立的弱边缘最终完成边缘检测。

下面详细介绍每一步的实现思路。

3.1 高斯平滑滤波

为了尽可能减少噪声对边缘检测结果的影响，所以必须滤除噪声以防止由噪声引起的错误检测。为了平滑图像，使用高斯滤波器与图像进行卷积，该步骤将平滑图像，以减少边缘检测器上明显的噪声影响。大小为(2k+1)x(2k+1)的高斯滤波器核的生成方程式由下式给出：

   

下面是一个sigma = 1.4，尺寸为3x3的高斯卷积核的例子（需要注意归一化）：

若图像中一个3x3的窗口为A，要滤波的像素点为e，则经过高斯滤波之后，像素点e的亮度值为：

 其中*为卷积符号，sum表示矩阵中所有元素相加求和。

重要的是需要理解，高斯卷积核大小的选择将影响Canny检测器的性能。尺寸越大，检测器对噪声的敏感度越低，但是边缘检测的定位误差也将略有增加。一般5x5是一个比较不错的trade off。

3.2 计算梯度强度和方向

图像中的边缘可以指向各个方向，因此Canny算法使用四个算子来检测图像中的水平、垂直和对角边缘。边缘检测的算子（如Roberts，Prewitt，Sobel等）返回水平Gx和垂直Gy方向的一阶导数值，由此便可以确定像素点的梯度G和方向theta 。

其中G为梯度强度， theta表示梯度方向，arctan为反正切函数。下面以Sobel算子为例讲述如何计算梯度强度和方向。

x和y方向的Sobel算子分别为：

其中Sx表示x方向的Sobel算子，用于检测y方向的边缘； Sy表示y方向的Sobel算子，用于检测x方向的边缘（边缘方向和梯度方向垂直）。在直角坐标系中，Sobel算子的方向如下图所示。

图3-1 Sobel算子的方向

 若图像中一个3x3的窗口为A，要计算梯度的像素点为e，则和Sobel算子进行卷积之后，像素点e在x和y方向的梯度值分别为： 

 

其中*为卷积符号，sum表示矩阵中所有元素相加求和。根据公式（3-2）便可以计算出像素点e的梯度和方向。

3.3 非极大值抑制

非极大值抑制是一种边缘稀疏技术，非极大值抑制的作用在于“瘦”边。对图像进行梯度计算后，仅仅基于梯度值提取的边缘仍然很模糊。对于标准3，对边缘有且应当只有一个准确的响应。而非极大值抑制则可以帮助将局部最大值之外的所有梯度值抑制为0，对梯度图像中每个像素进行非极大值抑制的算法是：

1)        将当前像素的梯度强度与沿正负梯度方向上的两个像素进行比较。

2)        如果当前像素的梯度强度与另外两个像素相比最大，则该像素点保留为边缘点，否则该像素点将被抑制。

通常为了更加精确的计算，在跨越梯度方向的两个相邻像素之间使用线性插值来得到要比较的像素梯度，现举例如下：

　　　　　　　　　　图3-2 梯度方向分割

如图3-2所示，将梯度分为8个方向，分别为E、NE、N、NW、W、SW、S、SE，其中0代表00~45o,1代表450~90o，2代表-900~-45o，3代表-450~0o。像素点P的梯度方向为theta，则像素点P1和P2的梯度线性插值为： 

因此非极大值抑制的伪代码描写如下：

 

需要注意的是，如何标志方向并不重要，重要的是梯度方向的计算要和梯度算子的选取保持一致。

3.4 双阈值检测

在施加非极大值抑制之后，剩余的像素可以更准确地表示图像中的实际边缘。然而，仍然存在由于噪声和颜色变化引起的一些边缘像素。为了解决这些杂散响应，必须用弱梯度值过滤边缘像素，并保留具有高梯度值的边缘像素，可以通过选择高低阈值来实现。如果边缘像素的梯度值高于高阈值，则将其标记为强边缘像素；如果边缘像素的梯度值小于高阈值并且大于低阈值，则将其标记为弱边缘像素；如果边缘像素的梯度值小于低阈值，则会被抑制。阈值的选择取决于给定输入图像的内容。

双阈值检测的伪代码描写如下：

3.5 抑制孤立低阈值点

到目前为止，被划分为强边缘的像素点已经被确定为边缘，因为它们是从图像中的真实边缘中提取出来的。然而，对于弱边缘像素，将会有一些争论，因为这些像素可以从真实边缘提取也可以是因噪声或颜色变化引起的。为了获得准确的结果，应该抑制由后者引起的弱边缘。通常，由真实边缘引起的弱边缘像素将连接到强边缘像素，而噪声响应未连接。为了跟踪边缘连接，通过查看弱边缘像素及其8个邻域像素，只要其中一个为强边缘像素，则该弱边缘点就可以保留为真实的边缘。

抑制孤立边缘点的伪代码描述如下：

4 总结

通过以上5个步骤即可完成基于Canny算法的边缘提取，图5-1是该算法的检测效果图，希望对大家有所帮助。

 　　　　　　　　　　　　　　　　　　　　　　　　图5-1 Canny边缘检测效果

 

Harris角点检测

下面有两幅不同视角的图像，通过找出对应的角点进行匹配。

 

再看下图所示，放大图像的两处角点区域：

我们可以直观的概括下角点所具有的特征：

>轮廓之间的交点；

>对于同一场景，即使视角发生变化，通常具备稳定性质的特征；

>该点附近区域的像素点无论在梯度方向上还是其梯度幅值上有着较大变化；

 

2. 角点检测算法基本思想是什么？

算法基本思想是使用一个固定窗口在图像上进行任意方向上的滑动，比较滑动前与滑动后两种情况，窗口中的像素灰度变化程度，如果存在任意方向上的滑动，都有着较大灰度变化，那么我们可以认为该窗口中存在角点。

3.如何用数学方法去刻画角点特征？

当窗口发生[u,v]移动时，那么滑动前与滑动后对应的窗口中的像素点灰度变化描述如下：

公式解释：

>[u,v]是窗口的偏移量

>(x,y)是窗口内所对应的像素坐标位置，窗口有多大，就有多少个位置

>w(x,y)是窗口函数，最简单情形就是窗口内的所有像素所对应的w权重系数均为1。但有时候，我们会将w(x,y)函数设定为以窗口中心为原点的二元正态分布。如果窗口中心点是角点时，移动前与移动后，该点的灰度变化应该最为剧烈，所以该点权重系数可以设定大些，表示窗口移动时，该点在灰度变化贡献较大；而离窗口中心(角点)较远的点，这些点的灰度变化几近平缓，这些点的权重系数，可以设定小点，以示该点对灰度变化贡献较小，那么我们自然想到使用二元高斯函数来表示窗口函数，这里仅是个人理解，大家可以参考下。

所以通常窗口函数有如下两种形式：

根据上述表达式，当窗口处在平坦区域上滑动，可以想象的到，灰度不会发生变化，那么E(u,v) = 0；如果窗口处在比纹理比较丰富的区域上滑动，那么灰度变化会很大。算法最终思想就是计算灰度发生较大变化时所对应的位置，当然这个较大是指针任意方向上的滑动，并非单指某个方向。

 

4.E(u,v)表达式进一步演化

首先需要了解泰勒公式，任何一个函数表达式，均可有泰勒公式进行展开，以逼近原函数，我们可以对下面函数进行一阶展开(如果对泰勒公式忘记了，可以翻翻本科所学的高等数学)

那么，

所以E(u,v)表达式可以更新为：

这里矩阵M为，

5.矩阵M的关键性

Harris角点检测并没有这样做，而是通过对窗口内的每个像素的x方向上的梯度与y方向上的梯度进行统计分析。这里以Ix和Iy为坐标轴，因此每个像素的梯度坐标可以表示成(Ix,Iy)。针对平坦区域，边缘区域以及角点区域三种情形进行分析：

下图是对这三种情况窗口中的对应像素的梯度分布进行绘制：

如果使用椭圆进行数据集表示，则绘制图示如下：

不知道大家有没有注意到这三种区域的特点，平坦区域上的每个像素点所对应的(IX,IY)坐标分布在原点附近，其实也很好理解，针对平坦区域的像素点，他们的梯度方向虽然各异，但是其幅值都不是很大，所以均聚集在原点附近；边缘区域有一坐标轴分布较散，至于是哪一个坐标上的数据分布较散不能一概而论，这要视边缘在图像上的具体位置而定，如果边缘是水平或者垂直方向，那么Iy轴方向或者Ix方向上的数据分布就比较散；角点区域的x、y方向上的梯度分布都比较散。我们是不是可以根据这些特征来判断哪些区域存在角点呢？

虽然我们利用E(u,v)来描述角点的基本思想，然而最终我们仅仅使用的是矩阵M。让我们看看矩阵M形式，是不是跟协方差矩阵形式很像，像归像，但是还是有些不同，哪儿不同？一般协方差矩阵对应维的随机变量需要减去该维随机变量的均值，但矩阵M中并没有这样做，所以在矩阵M里，我们先进行各维的均值化处理，那么各维所对应的随机变量的均值为0，协方差矩阵就大大简化了，简化的最终结果就是矩阵M，是否明白了？我们的目的是分析数据的主要成分，相信了解PCA原理的，应该都了解均值化的作用。

如果我们对协方差矩阵M进行对角化，很明显，特征值就是主分量上的方差，这点大家应该明白吧？不明白的话可以复习下PCA原理。如果存在两个主分量所对应的特征值都比较大，说明什么？ 像素点的梯度分布比较散，梯度变化程度比较大，符合角点在窗口区域的特点；如果是平坦区域，那么像素点的梯度所构成的点集比较集中在原点附近，因为窗口区域内的像素点的梯度幅值非常小，此时矩阵M的对角化的两个特征值比较小；如果是边缘区域，在计算像素点的x、y方向上的梯度时，边缘上的像素点的某个方向的梯度幅值变化比较明显，另一个方向上的梯度幅值变化较弱，其余部分的点都还是集中原点附近，这样M对角化后的两个特征值理论应该是一个比较大，一个比较小，当然对于边缘这种情况，可能是呈45°的边缘，致使计算出的特征值并不是都特别的大，总之跟含有角点的窗口的分布情况还是不同的。

注：M为协方差矩阵，需要大家自己去理解下，窗口中的像素集构成一个矩阵（2*n，假设这里有n个像素点），使用该矩阵乘以该矩阵的转置，即是协方差矩阵

因此可以得出下列结论：

>特征值都比较大时，即窗口中含有角点

>特征值一个较大，一个较小，窗口中含有边缘

>特征值都比较小，窗口处在平坦区域

6. 如何度量角点响应？

通常用下面表达式进行度量：

其中k是常量，一般取值为0.04~0.06，这个参数仅仅是这个函数的一个系数，它的存在只是调节函数的形状而已。

但是为什么会使用这样的表达式呢？一下子是不是感觉很难理解？其实也不难理解，函数表达式一旦出来，我们就可以绘制它的图像，而这个函数图形正好满足上面几个区域的特征。 通过绘制函数图像，直观上更能理解。绘制的R函数图像如下：

 

 

 

Hough变换简介

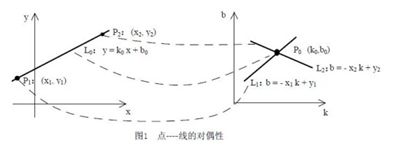
       Hough变换是图像处理中从图像中识别几何形状的基本方法之一。Hough变换的基本原理在于利用点与线的对偶性，将原始图像空间的给定的曲线通过曲线表达形式变为参数空间的一个点。这样就把原始图像中给定曲线的检测问题转化为寻找参数空间中的峰值问题。也即把检测整体特性转化为检测局部特性。比如直线、椭圆、圆、弧线等。

       霍夫变换于1962年由Paul Hough 首次提出[53]，后于1972年由Richard Duda和Peter Hart推广使用[54]，经典霍夫变换用来检测图像中的直线，后来霍夫变换扩展到任意形状物体的识别，多为圆和椭圆。

1.1 直线检测

       设已知一黑白图像上画了一条直线，要求出这条直线所在的位置。我们知道，直线的方程可以用y=k*x+b 来表示，其中k和b是参数，分别是斜率和截距。过某一点(x0,y0)的所有直线的参数都会满足方程y0=kx0+b。即点(x0,y0)确定了一族直线。方程y0=kx0+b在参数k--b平面上是一条直线，(你也可以是方程b=-x0*k+y0对应的直线)。这样，图像x--y平面上的一个前景像素点就对应到参数平面上的一条直线。我们举个例子说明解决前面那个问题的原理。设图像上的直线是y=x, 我们先取上面的三个点：A(0,0), B(1,1), C(22)。可以求出，过A点的直线的参数要满足方程b=0, 过B点的直线的参数要满足方程1=k+b, 过C点的直线的参数要满足方程2=2k+b, 这三个方程就对应着参数平面上的三条直线，而这三条直线会相交于一点(k=1,b=0)。　同理，原图像上直线y=x上的其它点(如(3,3),(4,4)等)　对应参数平面上的直线也会通过点(k=1,b=0)。这个性质就为我们解决问题提供了方法，就是把图像平面上的点对应到参数平面上的线，最后通过统计特性来解决问题。假如图像平面上有两条直线，那么最终在参数平面上就会看到两个峰值点，依此类推。

       简而言之，Hough变换思想为：在原始图像坐标系下的一个点对应了参数坐标系中的一条直线，同样参数坐标系的一条直线对应了原始坐标系下的一个点，然后，原始坐标系下呈现直线的所有点，它们的斜率和截距是相同的，所以它们在参数坐标系下对应于同一个点。这样在将原始坐标系下的各个点投影到参数坐标系下之后，看参数坐标系下有没有聚集点，这样的聚集点就对应了原始坐标系下的直线。

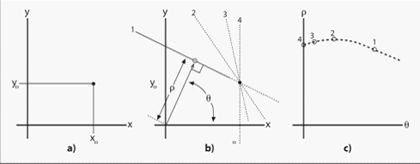
       在实际应用中，y=k*x+b形式的直线方程没有办法表示x=c形式的直线(这时候，直线的斜率为无穷大)。所以实际应用中，是采用参数方程p=x*cos(theta)+y*sin(theta)。这样，图像平面上的一个点就对应到参数p---theta平面上的一条曲线上，其它的还是一样。

   

上图（a）所示为原始的图像空间中一个点；（b）所示为直角坐标系当中为过同一四条直线；（c）所示为这四条直线在极坐标参数空间可以表示为四个点

      为了检测出直角坐标X-Y中由点所构成的直线，可以将极坐标a-p量化成许多小格。根据直角坐标中每个点的坐标(x,y)，在a = 0-180°内以小格的步长计算各个p值，所得值落在某个小格内，便使该小格的累加记数器加1。当直角坐标中全部的点都变换后，对小格进行检验，计数值最大的小格，其(a，p)值对应于直角坐标中所求直线。

 

思路解析：

1）读取一幅带处理二值图像，最好背景为黑色；

2）获取图像空间的源像素数据；

3）通过量化霍夫参数空间为有限个值间隔等分或者累加格子，即p,theta；

4）霍夫变换算法开始，每个像素坐标点P(x, y)被转换到(r, theta)的曲线点上面，并累加到对应的格子数据点；

5）寻找最大霍夫值，设置阈值，反变换到图像空间；

实际应用例子:车道检测

1.2 已知半径的圆

       其实Hough变换可以检测任意的已知表达形式的曲线，关键是看其参数空间的选择，参数空间的选择可以根据它的表达形式而定。比如圆的表达形式为 ，所以当检测某一半径的圆的时候，可以选择与原图像空间同样的空间作为参数空间。那么圆图像空间中的一个圆对应了参数空间中的一个点，参数空间中的一个点对应了图像空间中的一个圆，圆图像空间中在同一个圆上的点，它们的参数相同即a，b相同，那么它们在参数空间中的对应的圆就会过同一个点（a，b），所以，将原图像空间中的所有点变换到参数空间后，根据参数空间中点的聚集程度就可以判断出图像空间中有没有近似于圆的图形。如果有的话，这个参数就是圆的参数。

1.3 未知半径的圆

       对于圆的半径未知的情况下，可以看作是有三个参数的圆的检测，中心和半径。这个时候原理仍然相同，只是参数空间的维数升高，计算量增大。图像空间中的任意一个点都对应了参数空间中的一簇圆曲线。 ，其实是一个圆锥型。参数空间中的任意一个点对应了图像空间中的一个圆。

1.4 椭圆

      椭圆有5个自由参数，所以它的参数空间是5维的，因此他的计算量非常大，所以提出了许多的改进算法。

二、程序实现

　　对于处理一般图像，需要对图像进行边缘检测和二值化处理,Hough变换的输入是黑白二值图像。

　　matlab：

　　http://www.mathworks.cn/cn/help/images/ref/hough.html

　　openCV:

　　http://blog.csdn.net/ccxcau/article/details/7816588

 

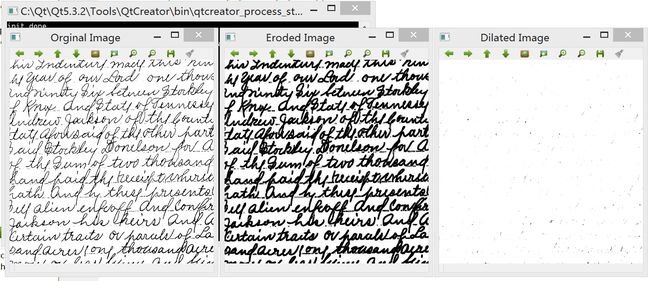
这里你会觉得腐蚀与膨胀、开操作与闭操作的效果和期望是相反的。这是因为我们认为图像素材中黑色字体是前景，白色为背景。而一般的，形态学规定用高像素表示前景物体，用低像素表示背景，因此使用这些基本运算之前，可以根据实际情况给原图像取反。

二、利用形态学滤波进行边缘检测

形态学滤波利用梯度进行边缘检测，其原理是计算膨胀后的图像和腐蚀后的图像的差值，由于两个变换后的图像不同之处主要在边缘处，图像边缘将通过求差得到强化。函数为morphologyEx，参数为MORPH_GRADIENT。若架构元素尺寸越大，检测出的边缘越厚。最简单的边缘检测运算是用原图减去腐蚀后的图像，或者用膨胀后的图像减去原图或腐蚀图像，效果很直观，缺点是得到的边缘较薄。

以下给出形态学滤波进行边缘检测的基本方法： 

效果差强人意……除此之外，还可以用sobel算子、Canny算子等对图像进行边缘检测，这些方法都可以通过改变结构元素来实现，如下图所示为几种3*3的Sobel算子。基于Sobel算子的边缘检测见：http://blog.csdn.net/liyuefeilong/article/details/43452711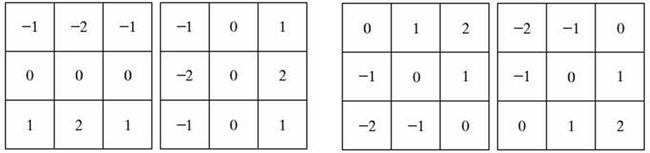 

另外一个应用是对图像进行形态学tophat变换，用h表示，定义为： 
 
其中，f是输入图像，B是结构元素函数。tophat变换对于增强灰度图像的阴影细节很有用处。

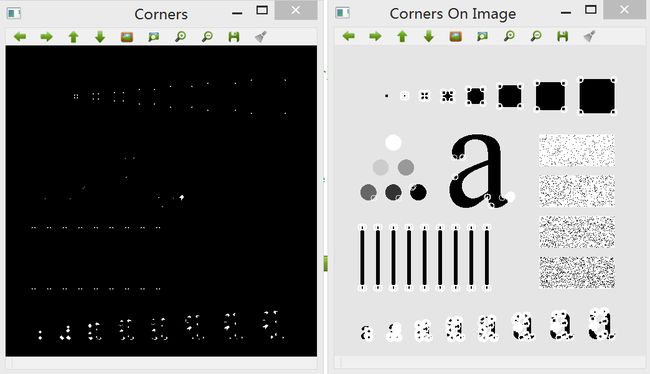
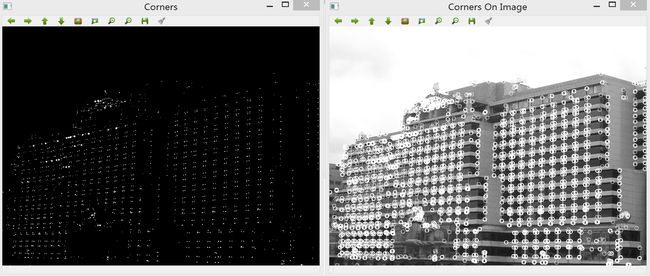
三、利用形态学滤波进行图像角点检测

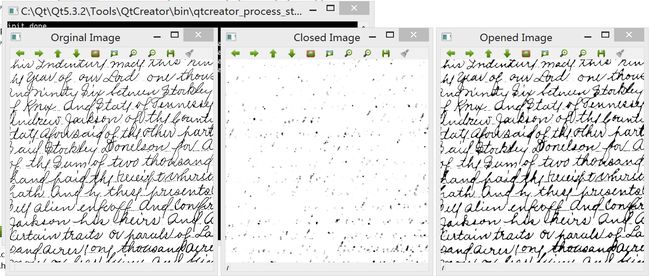
这里使用四种不同的结构元素检测图像角点，分别为十字型、菱型、x型和方形元素，尺寸规定为5*5。与边缘检测不同，角点的检测复杂。运算过程主要分三步：

第一步，先用十字形的结构元素膨胀原图像，这种情况下只会在边缘处“扩张”，角点不发生变化。接着用菱形的结构元素腐蚀原图像，只有拐角处才会被“收缩”，而直线边缘不发生变化。

第二步，用X型的结构元素膨胀原图像，角点膨胀的比边要多。这样第二次用方块腐蚀时，角点恢复原状，而边要腐蚀的更多。

第三步，将一二步的两幅输出图像相减，结果只保留了各个拐角处的细节。

 

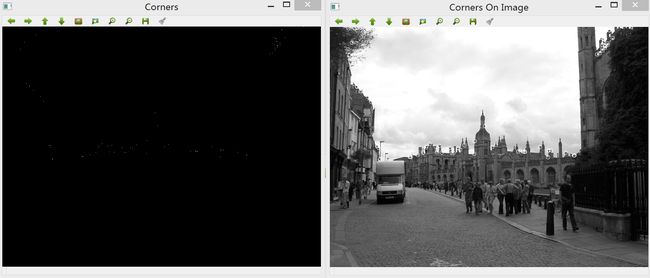
在这里，需要把输入图像转化为二值图像，因此阈值的选择会影响角点检测效果，如下图所示：

尽管角点检测效果有好有坏，不过实现该方法，对于理解腐蚀、膨胀、开操作、闭操作有很好的帮助。