剑指offer | 面试题40:最小的k个数
转载本文章请标明作者和出处
本文出自《Darwin的程序空间》
本文题目和部分解题思路来源自《剑指offer》第二版
![]()
题目
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4;
-
示例1
输入:arr = [3,2,1], k = 2 输出:[1,2] 或者 [2,1] -
示例2
输入:arr = [0,1,2,1], k = 1 输出:[0]
解题分析
这道题,拿到的第一个反应,就是先排序,然后取前K个数,这样时间复杂度也只是排序消耗的O(nlgn),但是人家只要最小的k个数,而你却排序了所有的数字,所以我们可以利用堆排序的原理,来构建K次大堆顶来解决这个问题;
堆和完全二叉树
-
什么是堆
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象;
-
什么是完全二叉树
正常的满二叉树应该是第一层一个节点,第二层两个,第三层四个… 每层有2^(n-1)个节点,完全二叉树允许最后一层右边有几个节点的缺失,但是最后一层中间不能断节点,也就是说其他层的节点数都必须是满的,而最后一层左边是必须连续的,右边可以有几个遗漏的, -
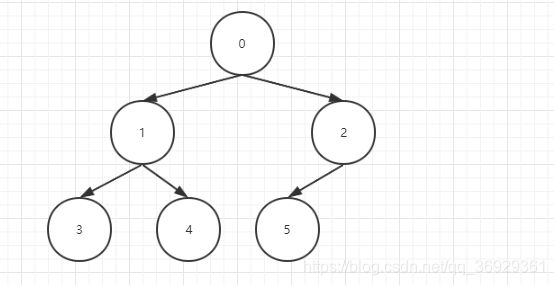
那么这样的二叉树是怎么被看成数组对象的,如下图,如果给一个完全二叉树从上到下,从左到右依次用从0开始的索引标记,就可以看做这颗完全二叉树也可以标识一个数组索引值也就是数组的下标值,下图即可标识[0,1,2,3,4,5]的数组;
-
完全二叉树的特性:
- 最后一个非叶子节点(也就是有子节点的节点)的坐标是n / 2 - 1,n为这颗二叉树的节点总数,以如下完全二叉树举例,最后一个非叶子节点是节点2,2 = 6 / 2 - 1 ,这里的除法是整除,python中就是n // 2 - 1;
- 如有一个节点有左右两个子节点,那么这两个节点的索引一定是2 * i + 1和2 * i + 2
堆排序
由上我们可以知道,堆其实就是一种完全二叉树,也可以用数组来标识,那么又有两种堆比较特殊,分别是大顶堆和小顶堆;
大顶堆就是二叉树的每个节点都比它的左右节点要大,而小顶堆就是每个节点都比其左右节点要小;
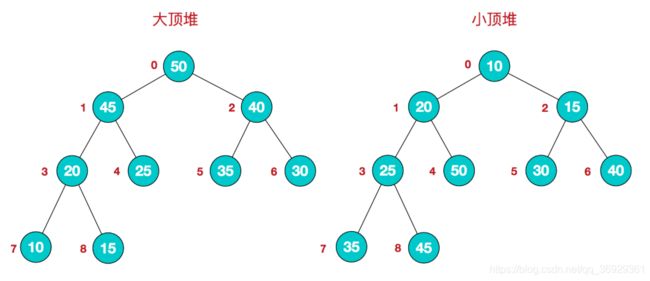
基于大顶堆的性质来说,最大的元素一定在整棵树的跟节点的位置,小堆顶则是最小的元素在整颗树的跟节点;
而堆排序正是使用了这个原理,首先我们从最后一个非叶子节点,也就是n/2-1的节点处,构建这最后一个非叶子节点为根节点的子树为大顶堆,然后再依次把从右到左,从下到上,依次递减大顶堆子树,最后整颗树即为大顶堆,然后我们把最大的元素和整个二叉树最末的位置交换,再屏蔽掉最后一个元素,然后以剩下的元素在置为大顶堆,这时候从节点0开始即可,因为其他的子树已经是大顶堆了,一次类推,每次都把最大的元素沉到数组末尾,即可完成排序;
我们以示例中给的[4、5、1、6、2、7、3、8],这个数组对应的堆,也就是完全二叉树如下
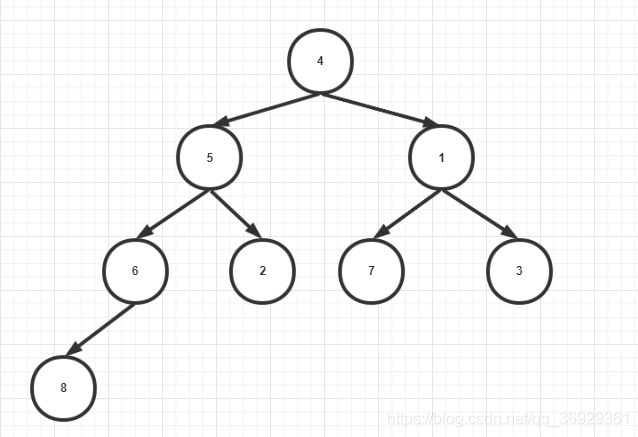
- 首先我们找出第一个非叶子节点为8 / 2 - 1= 3,下标索引3也就是节点6,我们对比节点6和节点8,发现8比6大,所以交换节点8和节点6的位置,这样这颗子树就形成了一个大顶堆

- 然后我们去到下一个飞叶子节点为3-1=2,也就是节点1,我们对比节点1的两个叶子节点7和3,明显7比较大,然后7再和1比,还是节点7比较大,所以节点7和节点1交换位置,这颗树也形成大顶堆;
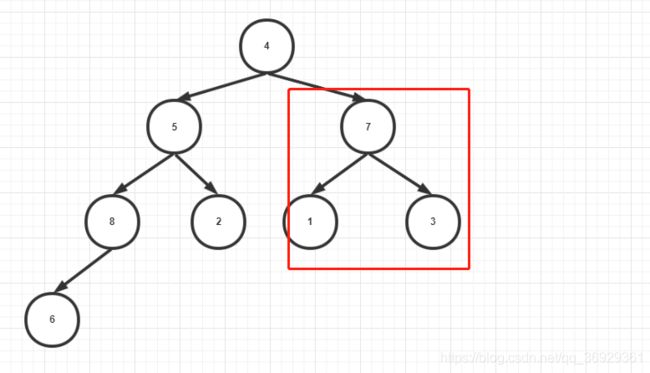
- 然后是节点5,它只需要和节点8和2比,因为节点8的子树已经置换大顶堆,节点8即为最大值,但是节点5被置换下来了,那么原来的大顶堆就不存在了,那么节点5和节点6的子树又要重新置换;
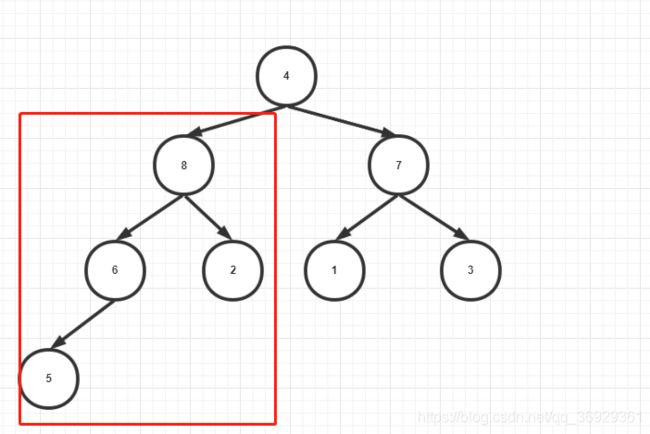
- 节点4也重复置换过程,最后结果是
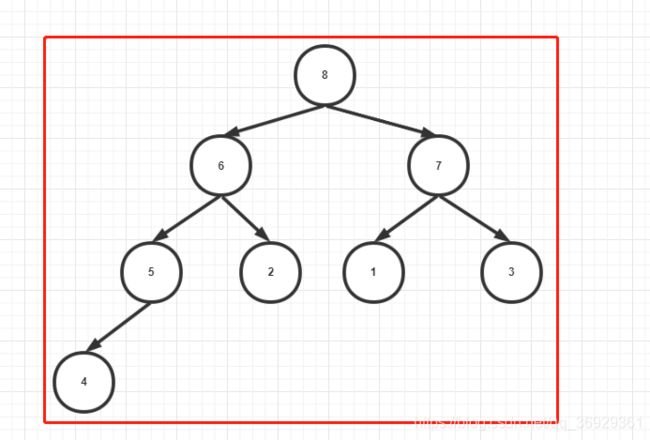
- 这样整棵树都是一个大顶堆,最大的元素8被置换到了最上面,然后我们把8和4交换,把4屏蔽,再继续置换,以此类推…
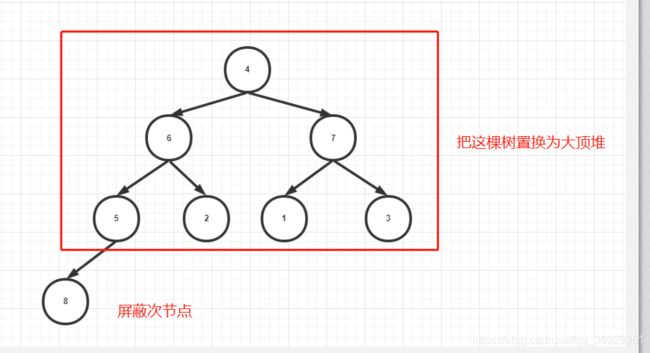
- 这样最大的元素一次被沉到树的末尾,也是数组的末尾,即可完成排序
最小的k个数
最小的k个数,我们可以直接取数组的前k个形成大顶堆,然后最的数即在索引0的位置arr[0],然后我们依次遍历剩下的数和索引0的比较,比它大的直接省略,比它小的和arr[0]互换,再次形成大顶堆,这样完事之后,索引0及是第k小的节点,前k个元素即时最小的k个元素,这样我们就可以减少构建顶堆的次数,完成代码的优化。
代码
ps:这里笔者使用的jdk为1.8、Python3.7版本
- java实现
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (Objects.isNull(arr) || arr.length < k) {
return new int[0];
}
if (arr.length == k) {
return arr;
}
for (int i = k / 2 - 1; i >= 0; i--) {
replacementHeap(arr, i, k - 1);
}
for (int i = k; i < arr.length; i++) {
if (arr[i] < arr[0]) {
arr[0] = arr[i];
replacementHeap(arr, 0, k - 1);
}
}
int[] result = new int[k];
System.arraycopy(arr, 0, result, 0, k);
return result;
}
private void replacementHeap(int[] arr, int index, int length) {
for (int i = index * 2 + 1; i <= length; i = i * 2 + 1) {
int temp = arr[index];
if (i + 1 <= length && arr[i + 1] > arr[i]) {
i += 1;
}
if (arr[i] > temp) {
arr[index] = arr[i];
arr[i] = temp;
}
index = i;
}
}
}
- Python实现
class Solution:
def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
if arr is None or len(arr) < k:
return []
if len(arr) == k:
return arr
y = k // 2 - 1
while y >= 0:
self.adjust_heap(arr, y, k)
y -= 1
for i in range(k, len(arr)):
if arr[i] < arr[0]:
arr[0] = arr[i]
self.adjust_heap(arr, 0, k)
return arr[:k]
def adjust_heap(self, arr, index, length):
i = index
child = i * 2 + 1
while i < length and child < length:
if child + 1 < length and arr[child + 1] > arr[child]:
child += 1
if arr[child] > arr[i]:
arr[child], arr[i] = arr[i], arr[child]
i = child
child = child * 2 + 1
![]()