剑指 Offer 41. 数据流中的中位数(python)
剑指 Offer 41. 数据流中的中位数
- 题目
- 思路
- 解法
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/shu-ju-liu-zhong-de-zhong-wei-shu-lcof
题目
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例 1:
输入:
[“MedianFinder”,“addNum”,“addNum”,“findMedian”,“addNum”,“findMedian”]
[[],[1],[2],[],[3],[]]
输出:[null,null,null,1.50000,null,2.00000]
示例 2:
输入:
[“MedianFinder”,“addNum”,“findMedian”,“addNum”,“findMedian”]
[[],[2],[],[3],[]]
输出:[null,null,2.00000,null,2.50000]
# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()
思路
要求随时可以提取一段数据流中的中位数,由题意可知,分两种情况:数据流个数为奇数,或者数据流个数为偶数。
我们可以想像,一串数据,我们以中间为节点切成两段,我们要求随时可以提取其中一段的顶部,或者两端的顶部求平均值。
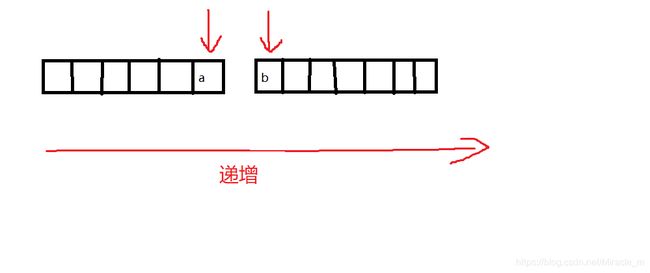
如上图所示,如果保持整个数据有序(这里设置为递增)则,a比左边都大,b比左边都小。维护某一段数据,保持有序,最常用的办法就是堆排序。
那么,我们分别用两个堆,维护左边较小的数,使之成为大顶堆;右边较大的数,使之成为小顶堆。
由于python中自带的堆为小顶堆,那么要构建大顶堆,只需要对需要维护的数据取反即可。(值得注意的是,进入堆和出堆的时候,都要取反)
解法
class MedianFinder:
def __init__(self):
"""
initialize your data structure here.
"""
self.A = []#维护较小数的大顶堆
self.B = []#维护较大数的小顶堆
def addNum(self, num: int) -> None:
# if self.A is None and self.B is None:
# heappush(self.A,-num)
# elif len(self.A)==len(self.B):
# heappush(self.B,num)
# heappush(self.A,-heappop(self.B))
# else:
# heappush(self.A,-num)
# heappush(self.B,-heappop(self.A))
############优化########################
if len(self.A)==len(self.B):
heappush(self.A,-heappushpop(self.B,num))
else:
heappush(self.B,-heappushpop(self.A,-num))
def findMedian(self) -> float:
if len(self.A)==len(self.B):
return (-self.A[0]+self.B[0])/2
else:return -self.A[0]
在python中,用heappushpop()比heappush(heappop())效率高很多很多!