伸展树 之 Java的实现
伸展树的介绍
伸展树(Splay Tree)是一种二叉排序树,它能在O(log n)内完成插入、查找和删除操作。它由Daniel Sleator和Robert Tarjan创造。
(01) 伸展树属于二叉查找树,即它具有和二叉查找树一样的性质:假设x为树中的任意一个结点,x节点包含关键字key,节点x的key值记为key[x]。如果y是x的左子树中的一个结点,则key[y] <= key[x];如果y是x的右子树的一个结点,则key[y] >= key[x]。
(02) 除了拥有二叉查找树的性质之外,伸展树还具有的一个特点是:当某个节点被访问时,伸展树会通过旋转使该节点成为树根。这样做的好处是,下次要访问该节点时,能够迅速的访问到该节点。
假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法,在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生,它是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
相比于”二叉查找树”和”AVL树”,学习伸展树时需要重点关注是”伸展树的旋转算法”。
伸展树的Java实现
1. 基本定义
public class SplayTree<T extends Comparable<T>> {
private SplayTreeNode mRoot; // 根结点
public class SplayTreeNode<T extends Comparable<T>> {
T key; // 关键字(键值)
SplayTreeNode left; // 左孩子
SplayTreeNode right; // 右孩子
public SplayTreeNode() {
this.left = null;
this.right = null;
}
public SplayTreeNode(T key, SplayTreeNode left, SplayTreeNode right) {
this.key = key;
this.left = left;
this.right = right;
}
}
...
} SplayTree是伸展树,而SplayTreeNode是伸展树节点。在此,我将SplayTreeNode定义为SplayTree的内部类。在伸展树SplayTree中包含了伸展树的根节点mRoot。SplayTreeNode包括的几个组成元素:
(01) key – 是关键字,是用来对伸展树的节点进行排序的。
(02) left – 是左孩子。
(03) right – 是右孩子。
2. 旋转
旋转是伸展树中需要重点关注的,它的代码如下:
/*
* 旋转key对应的节点为根节点,并返回根节点。
*
* 注意:
* (a):伸展树中存在"键值为key的节点"。
* 将"键值为key的节点"旋转为根节点。
* (b):伸展树中不存在"键值为key的节点",并且key < tree.key。
* b-1 "键值为key的节点"的前驱节点存在的话,将"键值为key的节点"的前驱节点旋转为根节点。
* b-2 "键值为key的节点"的前驱节点存在的话,则意味着,key比树中任何键值都小,那么此时,将最小节点旋转为根节点。
* (c):伸展树中不存在"键值为key的节点",并且key > tree.key。
* c-1 "键值为key的节点"的后继节点存在的话,将"键值为key的节点"的后继节点旋转为根节点。
* c-2 "键值为key的节点"的后继节点不存在的话,则意味着,key比树中任何键值都大,那么此时,将最大节点旋转为根节点。
*/
private SplayTreeNode splay(SplayTreeNode tree, T key) {
if (tree == null)
return tree;
SplayTreeNode N = new SplayTreeNode();
SplayTreeNode l = N;
SplayTreeNode r = N;
SplayTreeNode c;
for (;;) {
int cmp = key.compareTo(tree.key);
if (cmp < 0) {
if (tree.left == null)
break;
if (key.compareTo(tree.left.key) < 0) {
c = tree.left; /* rotate right */
tree.left = c.right;
c.right = tree;
tree = c;
if (tree.left == null)
break;
}
r.left = tree; /* link right */
r = tree;
tree = tree.left;
} else if (cmp > 0) {
if (tree.right == null)
break;
if (key.compareTo(tree.right.key) > 0) {
c = tree.right; /* rotate left */
tree.right = c.left;
c.left = tree;
tree = c;
if (tree.right == null)
break;
}
l.right = tree; /* link left */
l = tree;
tree = tree.right;
} else {
break;
}
}
l.right = tree.left; /* assemble */
r.left = tree.right;
tree.left = N.right;
tree.right = N.left;
return tree;
}
public void splay(T key) {
mRoot = splay(mRoot, key);
} 上面的代码的作用:将”键值为key的节点”旋转为根节点,并返回根节点。它的处理情况共包括:
(a):伸展树中存在”键值为key的节点”。
将”键值为key的节点”旋转为根节点。
(b):伸展树中不存在”键值为key的节点”,并且key < tree->key。
b-1) “键值为key的节点”的前驱节点存在的话,将”键值为key的节点”的前驱节点旋转为根节点。
b-2) “键值为key的节点”的前驱节点存在的话,则意味着,key比树中任何键值都小,那么此时,将最小节点旋转为根节点。
(c):伸展树中不存在”键值为key的节点”,并且key > tree->key。
c-1) “键值为key的节点”的后继节点存在的话,将”键值为key的节点”的后继节点旋转为根节点。
c-2) “键值为key的节点”的后继节点不存在的话,则意味着,key比树中任何键值都大,那么此时,将最大节点旋转为根节点。
下面列举个例子分别对a进行说明。
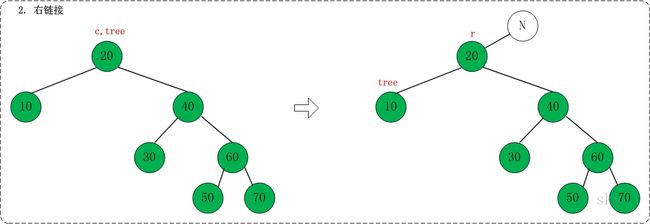
在下面的伸展树中查找10,,共包括”右旋” –> “右链接” –> “组合”这3步。
01, 右旋
对应代码中的”rotate right”部分
02, 右链接
对应代码中的”link right”部分
03. 组合
对应代码中的”assemble”部分
提示:如果在上面的伸展树中查找”70”,则正好与”示例1”对称,而对应的操作则分别是”rotate left”, “link left”和”assemble”。
其它的情况,例如”查找15是b-1的情况,查找5是b-2的情况”等等,这些都比较简单,大家可以自己分析。
3. 插入
插入代码
/*
* 将结点插入到伸展树中,并返回根节点
*
* 参数说明:
* tree 伸展树的
* z 插入的结点
*/
private SplayTreeNode insert(SplayTreeNode tree, SplayTreeNode z) {
int cmp;
SplayTreeNode y = null;
SplayTreeNode x = tree;
// 查找z的插入位置
while (x != null) {
y = x;
cmp = z.key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else {
System.out.printf("不允许插入相同节点(%d)!\n", z.key);
z=null;
return tree;
}
}
if (y==null)
tree = z;
else {
cmp = z.key.compareTo(y.key);
if (cmp < 0)
y.left = z;
else
y.right = z;
}
return tree;
}
public void insert(T key) {
SplayTreeNode z=new SplayTreeNode(key,null,null);
// 如果新建结点失败,则返回。
if ((z=new SplayTreeNode(key,null,null)) == null)
return ;
// 插入节点
mRoot = insert(mRoot, z);
// 将节点(key)旋转为根节点
mRoot = splay(mRoot, key);
} insert(key)是提供给外部的接口,它的作用是新建节点(节点的键值为key),并将节点插入到伸展树中;然后,将该节点旋转为根节点。
insert(tree, z)是内部接口,它的作用是将节点z插入到tree中。insert(tree, z)在将z插入到tree中时,仅仅只将tree当作是一棵二叉查找树,而且不允许插入相同节点。
4. 删除
删除代码
/*
* 删除结点(z),并返回被删除的结点
*
* 参数说明:
* bst 伸展树
* z 删除的结点
*/
private SplayTreeNode remove(SplayTreeNode tree, T key) {
SplayTreeNode x;
if (tree == null)
return null;
// 查找键值为key的节点,找不到的话直接返回。
if (search(tree, key) == null)
return tree;
// 将key对应的节点旋转为根节点。
tree = splay(tree, key);
if (tree.left != null) {
// 将"tree的前驱节点"旋转为根节点
x = splay(tree.left, key);
// 移除tree节点
x.right = tree.right;
}
else
x = tree.right;
tree = null;
return x;
}
public void remove(T key) {
mRoot = remove(mRoot, key);
} remove(key)是外部接口,remove(tree, key)是内部接口。
remove(tree, key)的作用是:删除伸展树中键值为key的节点。
它会先在伸展树中查找键值为key的节点。若没有找到的话,则直接返回。若找到的话,则将该节点旋转为根节点,然后再删除该节点。
关于”前序遍历”、”中序遍历”、”后序遍历”、”最大值”、”最小值”、”查找”、”打印伸展树”、”销毁伸展树”等接口就不再单独介绍了,Please RTFSC(Read The Fucking Source Code)!这些接口,与前面介绍的”二叉查找树”、”AVL树”的相关接口都是类似的。
伸展树的Java实现(完整源码)
伸展树的实现文件(SplayTree.java)
/**
* Java 语言: 伸展树
*
* @author skywang
* @date 2014/02/03
*/
public class SplayTree> {
private SplayTreeNode mRoot; // 根结点
public class SplayTreeNode> {
T key; // 关键字(键值)
SplayTreeNode left; // 左孩子
SplayTreeNode right; // 右孩子
public SplayTreeNode() {
this.left = null;
this.right = null;
}
public SplayTreeNode(T key, SplayTreeNode left, SplayTreeNode right) {
this.key = key;
this.left = left;
this.right = right;
}
}
public SplayTree() {
mRoot=null;
}
/*
* 前序遍历"伸展树"
*/
private void preOrder(SplayTreeNode tree) {
if(tree != null) {
System.out.print(tree.key+" ");
preOrder(tree.left);
preOrder(tree.right);
}
}
public void preOrder() {
preOrder(mRoot);
}
/*
* 中序遍历"伸展树"
*/
private void inOrder(SplayTreeNode tree) {
if(tree != null) {
inOrder(tree.left);
System.out.print(tree.key+" ");
inOrder(tree.right);
}
}
public void inOrder() {
inOrder(mRoot);
}
/*
* 后序遍历"伸展树"
*/
private void postOrder(SplayTreeNode tree) {
if(tree != null)
{
postOrder(tree.left);
postOrder(tree.right);
System.out.print(tree.key+" ");
}
}
public void postOrder() {
postOrder(mRoot);
}
/*
* (递归实现)查找"伸展树x"中键值为key的节点
*/
private SplayTreeNode search(SplayTreeNode x, T key) {
if (x==null)
return x;
int cmp = key.compareTo(x.key);
if (cmp < 0)
return search(x.left, key);
else if (cmp > 0)
return search(x.right, key);
else
return x;
}
public SplayTreeNode search(T key) {
return search(mRoot, key);
}
/*
* (非递归实现)查找"伸展树x"中键值为key的节点
*/
private SplayTreeNode iterativeSearch(SplayTreeNode x, T key) {
while (x!=null) {
int cmp = key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else
return x;
}
return x;
}
public SplayTreeNode iterativeSearch(T key) {
return iterativeSearch(mRoot, key);
}
/*
* 查找最小结点:返回tree为根结点的伸展树的最小结点。
*/
private SplayTreeNode minimum(SplayTreeNode tree) {
if (tree == null)
return null;
while(tree.left != null)
tree = tree.left;
return tree;
}
public T minimum() {
SplayTreeNode p = minimum(mRoot);
if (p != null)
return p.key;
return null;
}
/*
* 查找最大结点:返回tree为根结点的伸展树的最大结点。
*/
private SplayTreeNode maximum(SplayTreeNode tree) {
if (tree == null)
return null;
while(tree.right != null)
tree = tree.right;
return tree;
}
public T maximum() {
SplayTreeNode p = maximum(mRoot);
if (p != null)
return p.key;
return null;
}
/*
* 旋转key对应的节点为根节点,并返回根节点。
*
* 注意:
* (a):伸展树中存在"键值为key的节点"。
* 将"键值为key的节点"旋转为根节点。
* (b):伸展树中不存在"键值为key的节点",并且key < tree.key。
* b-1 "键值为key的节点"的前驱节点存在的话,将"键值为key的节点"的前驱节点旋转为根节点。
* b-2 "键值为key的节点"的前驱节点存在的话,则意味着,key比树中任何键值都小,那么此时,将最小节点旋转为根节点。
* (c):伸展树中不存在"键值为key的节点",并且key > tree.key。
* c-1 "键值为key的节点"的后继节点存在的话,将"键值为key的节点"的后继节点旋转为根节点。
* c-2 "键值为key的节点"的后继节点不存在的话,则意味着,key比树中任何键值都大,那么此时,将最大节点旋转为根节点。
*/
private SplayTreeNode splay(SplayTreeNode tree, T key) {
if (tree == null)
return tree;
SplayTreeNode N = new SplayTreeNode();
SplayTreeNode l = N;
SplayTreeNode r = N;
SplayTreeNode c;
for (;;) {
int cmp = key.compareTo(tree.key);
if (cmp < 0) {
if (tree.left == null)
break;
if (key.compareTo(tree.left.key) < 0) {
c = tree.left; /* rotate right */
tree.left = c.right;
c.right = tree;
tree = c;
if (tree.left == null)
break;
}
r.left = tree; /* link right */
r = tree;
tree = tree.left;
} else if (cmp > 0) {
if (tree.right == null)
break;
if (key.compareTo(tree.right.key) > 0) {
c = tree.right; /* rotate left */
tree.right = c.left;
c.left = tree;
tree = c;
if (tree.right == null)
break;
}
l.right = tree; /* link left */
l = tree;
tree = tree.right;
} else {
break;
}
}
l.right = tree.left; /* assemble */
r.left = tree.right;
tree.left = N.right;
tree.right = N.left;
return tree;
}
public void splay(T key) {
mRoot = splay(mRoot, key);
}
/*
* 将结点插入到伸展树中,并返回根节点
*
* 参数说明:
* tree 伸展树的
* z 插入的结点
*/
private SplayTreeNode insert(SplayTreeNode tree, SplayTreeNode z) {
int cmp;
SplayTreeNode y = null;
SplayTreeNode x = tree;
// 查找z的插入位置
while (x != null) {
y = x;
cmp = z.key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else {
System.out.printf("不允许插入相同节点(%d)!\n", z.key);
z=null;
return tree;
}
}
if (y==null)
tree = z;
else {
cmp = z.key.compareTo(y.key);
if (cmp < 0)
y.left = z;
else
y.right = z;
}
return tree;
}
public void insert(T key) {
SplayTreeNode z=new SplayTreeNode(key,null,null);
// 如果新建结点失败,则返回。
if ((z=new SplayTreeNode(key,null,null)) == null)
return ;
// 插入节点
mRoot = insert(mRoot, z);
// 将节点(key)旋转为根节点
mRoot = splay(mRoot, key);
}
/*
* 删除结点(z),并返回被删除的结点
*
* 参数说明:
* bst 伸展树
* z 删除的结点
*/
private SplayTreeNode remove(SplayTreeNode tree, T key) {
SplayTreeNode x;
if (tree == null)
return null;
// 查找键值为key的节点,找不到的话直接返回。
if (search(tree, key) == null)
return tree;
// 将key对应的节点旋转为根节点。
tree = splay(tree, key);
if (tree.left != null) {
// 将"tree的前驱节点"旋转为根节点
x = splay(tree.left, key);
// 移除tree节点
x.right = tree.right;
}
else
x = tree.right;
tree = null;
return x;
}
public void remove(T key) {
mRoot = remove(mRoot, key);
}
/*
* 销毁伸展树
*/
private void destroy(SplayTreeNode tree) {
if (tree==null)
return ;
if (tree.left != null)
destroy(tree.left);
if (tree.right != null)
destroy(tree.right);
tree=null;
}
public void clear() {
destroy(mRoot);
mRoot = null;
}
/*
* 打印"伸展树"
*
* key -- 节点的键值
* direction -- 0,表示该节点是根节点;
* -1,表示该节点是它的父结点的左孩子;
* 1,表示该节点是它的父结点的右孩子。
*/
private void print(SplayTreeNode tree, T key, int direction) {
if(tree != null) {
if(direction==0) // tree是根节点
System.out.printf("%2d is root\n", tree.key);
else // tree是分支节点
System.out.printf("%2d is %2d's %6s child\n", tree.key, key, direction==1?"right" : "left");
print(tree.left, tree.key, -1);
print(tree.right,tree.key, 1);
}
}
public void print() {
if (mRoot != null)
print(mRoot, mRoot.key, 0);
}
} 伸展树的测试程序(SplayTreeTest.java)
/**
* Java 语言: 伸展树
*
* @author skywang
* @date 2014/02/03
*/
public class SplayTreeTest {
private static final int arr[] = {10,50,40,30,20,60};
public static void main(String[] args) {
int i, ilen;
SplayTree tree=new SplayTree();
System.out.print("== 依次添加: ");
ilen = arr.length;
for(i=0; i
System.out.print(arr[i]+" ");
tree.insert(arr[i]);
}
System.out.print("\n== 前序遍历: ");
tree.preOrder();
System.out.print("\n== 中序遍历: ");
tree.inOrder();
System.out.print("\n== 后序遍历: ");
tree.postOrder();
System.out.println();
System.out.println("== 最小值: "+ tree.minimum());
System.out.println("== 最大值: "+ tree.maximum());
System.out.println("== 树的详细信息: ");
tree.print();
i = 30;
System.out.printf("\n== 旋转节点(%d)为根节点\n", i);
tree.splay(i);
System.out.printf("== 树的详细信息: \n");
tree.print();
// 销毁二叉树
tree.clear();
}
} 在二叉查找树的Java实现中,使用了泛型,也就意味着它支持任意类型;但是该类型必须要实现Comparable接口。
伸展树的Java测试程序
伸展树的测试程序运行结果如下:
== 依次添加: 10 50 40 30 20 60
== 前序遍历: 60 30 20 10 50 40
== 中序遍历: 10 20 30 40 50 60
== 后序遍历: 10 20 40 50 30 60
== 最小值: 10
== 最大值: 60
== 树的详细信息:
is root
is 60's left child
is 30's left child
is 20's left child
is 30's right child
is 50's left child
== 旋转节点(30)为根节点
== 树的详细信息:
is root
is 30's left child
is 20's left child
is 30's right child
is 60's left child
is 50's left child测试程序的主要流程是:新建伸展树,然后向伸展树中依次插入10,50,40,30,20,60。插入完毕这些数据之后,伸展树的节点是60;此时,再旋转节点,使得30成为根节点。
依次插入10,50,40,30,20,60示意图如下:
将30旋转为根节点的示意图如下:
转载自:伸展树(三)之 Java的实现