前言:Hello 大家好,我是小花,又和大家见面了,前面的文章一直是对机器学习的基本分类,回归,聚类算法进行学习。那时候我记得给了大家很多特征,当时我说,特征的好坏决定了机器学习算法的效果。那么接下来,我将会带着大家研究研究机器学习的特征。
这是我在ICML上看到的一篇文章,作者是华盛顿大学的一个教授,文章名:deep canonical correlation analysis。就是深度典型相关分析。目的是解决多视图学习的非线性问题。前面我的文章对这个有介绍:
多视图学习:http://www.cnblogs.com/xiaohuahua108/p/6014188.html
典型相关分析:http://www.cnblogs.com/xiaohuahua108/p/6086959.html
估计看到这里的小伙伴估计就要问了,等等,非线性问题,不是你在说SVM算法的时候,用核解决的么。哈哈,真聪明,我在把连接给大家。
核的介绍:http://www.cnblogs.com/xiaohuahua108/p/6146118.html
核的思想:将数据映射到更高维的空间,希望在这个更高维的空间中,数据可以变得更容易分离或更好的结构化。对这种映射的形式也没有约束,这甚至可能导致无限维空间。然而,这种映射函数几乎不需要计算的,所以可以说成是在低维空间计算高维空间内积的一个工具。
那小伙伴肯定说把核函数加到CCA上不就完美解决了非线性问题了么,那这个深度网络的CCA难道比核方法好?我们稍后再说。
核CCA,既然大家都想到了,核加CCA。那么我就把KCCA的优化表达式给大家:
那既然选择了这个Deep CCA,那这个是不是比KCCA好呢。大家应该知道,核方法的应用主要在于核选取的不可知性,还有计算量比较大。说了这么多,我们先来介绍这个方法吧。
一:深度神经网络
深度网络就是超过两层的神经网络。如下图:
二:深度典型相关分析
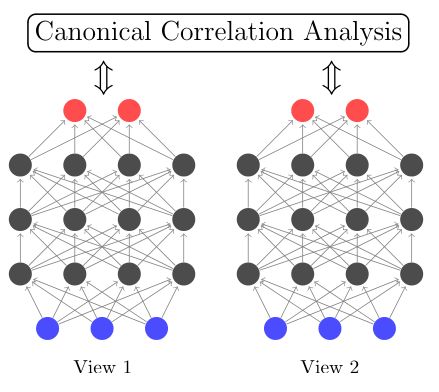
大家都知道,典型相关分析是一个物体的不同视图,然后通过求两个视图的最大相关性,然后把它们融合在一个子空间。但是这是传统的线性问题,如果数据是非线性的,用传统的CCA去算的话,效果可想而知不好。而神经网络解决非线性问题的时候,就是通过嵌入每个层次的非线性函数来解决的,Deep CCA就是先用深度神经网络分别求出两个视图的经过线性化的向量,然后求出两个投影向量的最大相关性,最后求出新的投影向量。用这个投影向量加入到机器学习算法进行分类,聚类回归。
三 操作流程
如下图,假设我们输入层有C1个单元,输出层有σ个单元。
那么第一个视图的第一层输出为:![]() 其中s是一个非线性函数。
其中s是一个非线性函数。![]() 为权重的一般性写法。v代表第几个视图,d代表网络的层次。
为权重的一般性写法。v代表第几个视图,d代表网络的层次。
第二层输出为:![]()
,,,
最后输出为:![]() 。
。
第二个视图的输出为:![]()
那么现在我们的优化目标就和CCA一样,只是把原先直接输入的特征集用深度网络训练一遍,然后在用CCA求出投影向量。
优化目标就是:![]() 其中
其中![]() 分别为第一视图与第二个视图的参数集合。
分别为第一视图与第二个视图的参数集合。
![]()
我们为了求出![]() ,用反向传播的理论。
,用反向传播的理论。
假设H1作为被深度网络训练之后的样本,同理H2也是。当然为了计算方便,我们把数据中心化![]() 分别为中心化之后的数据。
分别为中心化之后的数据。
那么视图一和视图二之间的协方差阵为:![]() (计算参照于秀林版的多元统计分析)
(计算参照于秀林版的多元统计分析)
视图一的协方差矩阵为:![]() 为了让矩阵有逆,类似于岭回归。其中r1是正则化参数,我一直认为叫正规化参数比较好理解。关于参数的选举我以后开一篇博客详细介绍下。
为了让矩阵有逆,类似于岭回归。其中r1是正则化参数,我一直认为叫正规化参数比较好理解。关于参数的选举我以后开一篇博客详细介绍下。
同理,视图二的协方差矩阵为:![]()
由于我们知道,整个相关性等于矩阵![]() .如果我们让K=σ,那么相关性就是矩阵T的迹范数也就是:
.如果我们让K=σ,那么相关性就是矩阵T的迹范数也就是:![]()
更具反向传播,以及奇异值分解,那么![]() ,
,
其中:![]()
![]()
至于后面的我就不说了,就是求出参数带进去算就可以了。
四 几个细节
因为是整个样本的相关系,不是分成一些数据点相关系的和。目前还不知道如何用随机优化方法一个一个地处理数据点。本篇文章采取的是一个基于最小批租的方法(Le, Q. V., Ngiam, J., Coates, A., Lahiri, A., Prochnow,B., and Ng, A. Y. On optimization methods for deeplearning. In ICML, 2011),但是比L-BFGS 方法要好,该方法来自(Nocedal, J. and Wright, S. J. Numerical Optimization.Springer, New York, 2nd edition, 2006)。
一开始训练的参数不是一个随机的初始化的参数,一般要先进行预训练。本文采取的初始参数方法是来自(Vincent, P., Larochelle, H., Bengio, Y., and Manzagol, P.-A.Extracting and composing robust features with denoisingautoencoders. In ICML. ACM)它是一个噪声的自编码技术。
另外在数据集进行处理的时候,加上一个方差为![]() 的高斯噪声作为样本集
的高斯噪声作为样本集![]() 。然后被重建的样本集为
。然后被重建的样本集为![]() ,然后用L-BFGS方法重建初始数据加上二次惩罚系数:
,然后用L-BFGS方法重建初始数据加上二次惩罚系数:
![]() ,然后W,b被用来做DCCA的优化,然后作为下一层的预训练。
,然后W,b被用来做DCCA的优化,然后作为下一层的预训练。
五 sigmoid函数的选择问题
任何一个非线性的sigmid都可以决定每个神经元的输出,但是这篇文章使用一个新的以立方根为基础的sigmid函数,设![]() 。则sigmoid函数为:
。则sigmoid函数为:![]() 。这个函数与传统的logistic和双曲正切非线性函数相比,S函数有一个s形状,和在x=0的时候有一个单位斜率,与双曲切面相比,他是一个新奇的功能,但是logistic和双曲切面值变化特别快。如下图:
。这个函数与传统的logistic和双曲正切非线性函数相比,S函数有一个s形状,和在x=0的时候有一个单位斜率,与双曲切面相比,他是一个新奇的功能,但是logistic和双曲切面值变化特别快。如下图:
另外一个是实现简单:这个s函数的导数很简单,实现起来比较方便。
六 总结
好了,本文说完了。可能理解有些偏颇,希望大家指正,哈哈。