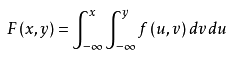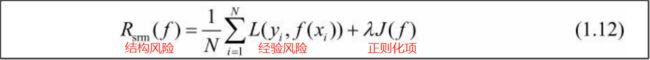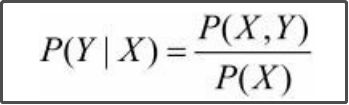【统计学习方法by李航】第一章 统计学习方法概论 个人总结
第一章 统计学习方法概论
- 开始的话
- 一、统计学习 [1.1]
- （一）总定义
- （二）统计学习的方法
- 二、监督学习[1.2]
- （一）基本概念[1.2.1]
- 1、输入空间、特征空间与输出空间
- 2、联合概率分布
- 3、假设空间（上面名词解释里面有讲）
- （二）问题的形式化[1.2.2]
- 三、统计学习三要素[1.3]
- （一）模型[1.3.1]
- （二）策略[1.3.2]
- 1、损失函数、代价函数
- 2、风险函数(期望损失)、经验风险(经验损失)【L是损失函数】
- 3、经验风险最小化(ERM)与结构风险最小化(SRM)
- （三）算法（略）
- 四、模型评估与模型选择[1.4]
- （一）训练误差与测试误差[1.4.1]
- （二）过拟合与模型选择[1.4.2]
- 五、正则化与交叉验证[1.5]
- （一）正则化[1.5.1]
- 1、正则化形式
- 2、范数
- （二）交叉验证[1.5.2]
- 1、简单交叉验证
- 2、S折交叉验证（有些地方叫k折交叉验证法）
- 3、留1交叉验证
- 六、泛化能力[1.6]
- （一）泛化误差[1.6.1]
- （二）泛化误差的概率上界（泛化误差上界）[1.6.2]
- （三）例子：二类分类问题的泛化误差上界（可以不用看）
- 七、生成模型与判别模型[1.7]
- 八、分类问题[1.8]
- 九、标注问题[1.9]
- 十、回归问题[1.10]
开始的话
尽量精简、总结，顺序重排
肯定会有些错漏之处
学到哪更到哪
半角方括号中的数字对应书中的章节
全角方括号 一般是前面文字的 总结
圆括号 是 补充说明
引用是 大段补充 或 例子
链接：[ 全文章目录 ]
一、统计学习 [1.1]
（一）总定义
统计学习：提取数据特征 ——> 抽象数据模型 ——> 对数据进行分析与预测
（二）统计学习的方法
统计学习的几类：
- 监督学习（supervised learning）【重点】：分类、标注、回归
- 非监督学习（unsupervised learning）：聚类、降维
- 半监督学习（semi-supervised learning）
- 强化学习（reinforcement learning）
- 补充：深度学习和神经网络
算法：略（这本书主要讲监督学习的算法，后面就会学到了）
本节名词理解：
-数据独立同分布：数据间相互独立，但遵循同一分布函数
-假设空间（hypothesis space）：假设要学习的模型属于某个函数的集合（比如模型就是一条一元一次的直线，你就不可能把它放在有小猪佩奇这么复杂的函数集合里面）
-评价标准（evaluation criterion）：后面会细讲
二、监督学习[1.2]
（一）基本概念[1.2.1]
1、输入空间、特征空间与输出空间
输入的是一个 实例（instance）
↓↓↓↓
一般由 特征向量（feature vector）表示
↓↓↓↓↓↓↓↓
特征向量的空间称为 特征空间（feature space）
【输入的是个向量，向量有几维就是几维空间】
2、联合概率分布
概率论知识：[ 百度百科链接 ]
例子：
3、假设空间（上面名词解释里面有讲）
符号：
条件概率分布P(Y|X)
决策函数（decision function）Y=f(X)
（二）问题的形式化[1.2.2]
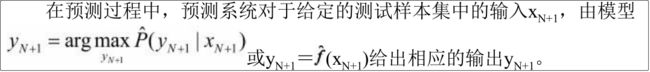
解释一下argmax()是什么：argmax = argument max，自变量最大值
x=argmax( f(x) )
argmax( f(x) )是使得 f(x)取得最大值所对应的变量x
本节名词理解：
-欧式空间（欧几里得空间）：就是几维空间，但是在这里，可以理解为有几个变量，有几个变量就是几维空间
三、统计学习三要素[1.3]
三要素：假设要什么模型【模型】 ——> 这模型有什么好【策略】 ——> 用什么算法算出这个模型【算法】
（一）模型[1.3.1]
决策函数表示的模型为非概率模型，
条件概率表示的模型为概率模型。
（二）策略[1.3.2]
[ 不同函数的区别 ]
要点：损失函数、经验风险、结构风险最小化
1、损失函数、代价函数
- 损失函数(loss function) 度量模型 一次 预测的好坏，
- 代价函数(cost function) 是损失函数的 代数总和 。
2、风险函数(期望损失)、经验风险(经验损失)【L是损失函数】
- Rexp：风险函数(risk function) 或期望损失(expected loss)是损失函数的 期望总和 。
（1.9）损失函数的期望 = ∑( 那点的损失 * 那点的概率 )
！！！ 但是，由于联合分布P(X, Y)是未知的，所以 风险函数不能直接计算 。
- Remp：经验风险(empirical risk)或经验损失(empirical loss)是损失函数对(相对)全部数据的 平均值 。【重点】
而当样本容量N趋于无穷时，经验风险趋于期望风险，一般数据集有限，所以经验风险估计期望风险不理想。
引出经验风险最小化以及结构风险最小化。
3、经验风险最小化(ERM)与结构风险最小化(SRM)
- 经验风险最小化：经验风险最小的模型是最优的模型。
极大似然估计是经验风险最小化的一个例子，当模型是条件概率分布，损失函数是对数损失函数的时候，经验风险最小化等价于极大似然估计。
！！！ 但是，如果样本小，使用经验风险最小化时可能就会产生 “过拟合” 现象。
- 结构风险最小化：在经验风险的基础上，加上正则化项或罚项 【重点】
正则化项下面会细讲。
贝叶斯估计中的最大后验概率估计（maximum posterior probability estimation，MAP）就是结构风险最小化的一个例子。当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时，结构风险最小化就等价于最大后验概率估计。
（三）算法（略）
四、模型评估与模型选择[1.4]
（一）训练误差与测试误差[1.4.1]
训练误差是模型对训练数据集的经验风险，
测试误差是模型对测试数据集的经验风险。
当损失函数是0-1损失时，测试误差就变成了常见的测试数据集上的误差率。（0-1损失：当输出的y与正确的y不相同时为1，反之为0）
对未知数据的预测能力称为泛化能力。
（二）过拟合与模型选择[1.4.2]
过拟合：
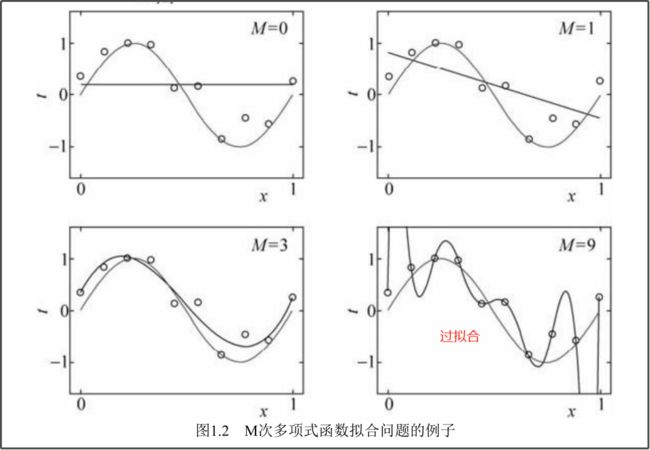
求经验损失最少：最小二乘法：略（）
为了尽量得到测试误差的最小值，引出正则化和交叉验证。
五、正则化与交叉验证[1.5]
（一）正则化[1.5.1]
1、正则化形式
跟上面 结构风险最小化 的图是一个东西。
λ>=0用以权衡经验风险和模型复杂度
J(f)为模型的复杂度。模型f越复杂，复杂度J(f)就越大，反之，就越小。
能够很好地解释已知数据并且 十分简单 才是最好的模型。
2、范数
L0范数：向量中非0元素的个数
L1范数：向量各元素的绝对值之和
L2范数：向量各元素的平方和然后开方
知道范数是什么后。再来理解下图。
（二）交叉验证[1.5.2]
1、简单交叉验证
把一块蛋糕分成两份（大小可不一，46、73都可以），用一份当作训练集，另一部分当作测试集(验证集)
2、S折交叉验证（有些地方叫k折交叉验证法）
例如S为10的时候，把蛋糕分成均等的10分并标上序号，分10次进行验证。
第n次：取第n份的蛋糕做测试集，其他9份做训练集。
3、留1交叉验证
你把蛋糕分成了S份，但是每1份里面只有一个向量。【S等于样本数】
六、泛化能力[1.6]
（一）泛化误差[1.6.1]
就是上面的风险函数（期望损失、期望风险）
（二）泛化误差的概率上界（泛化误差上界）[1.6.2]
性质：
1.它是样本容量的函数，当样本容量增加时，泛化上界趋于0；
2.它是假设空间容量（capacity）的函数，假设空间容量越大，模型就越难学，泛化误差上界就越大。
大白话：【样本容量越大，学习产生的模型对数据预测的误差越小；维数越高(变量越多)越难学】
（三）例子：二类分类问题的泛化误差上界（可以不用看）
证明：
1.
2.
代入
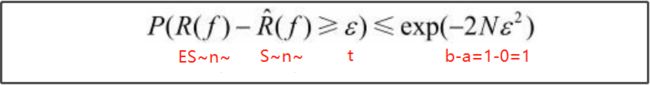
3.
P(a>=b)<=x ===》 1-P(a
由2中式子变化为:
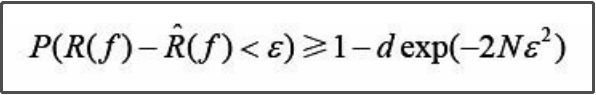
4.
定义一个变量δ（delta小写）化简
5.
对于外面那个“>=”号来说，至少有1-δ的概率
对P()里面的“<”号来说，“<”右边的就是左边泛化误差的上界，即泛化误差上界
放在一起讲，就是书中所说：
为什么说可以不用看呢，因为讨论的只是假设空间包含有限个函数情况下的泛化误差上界，而一般情况下，假设空间包含的函数都是无限的。
七、生成模型与判别模型[1.7]
模型的一般形式：
决策函数：Y＝f(X)
条件概率分布：P(Y|X)
统计学习方法：
-
生成方法——>生成模型——>学习得到联合概率分布P(x,y)
根据条件概率公式：
来生成生成模型。 -
判别方法——>判别模型——>学习得到条件概率分布P(y|x)或决策函数f(X)
书中列举的特点：
| 生成方法 | 判别方法 |
|---|---|
| 可以还原出联合概率分布P(X,Y) | 不能 |
| 当样本容量增加的时候，学到的模型可以更快收敛于真实模型 | 较慢 |
| 允许存在隐变量 | 不允许存在隐变量 |
| 往往学习的准确率更高 | |
| 可以对数据进行各种程度上的抽象、定义特征并使用特征，因此可以简化学习问题 |
链接：[ 生成模型和判别模型的具体区别 ]
八、分类问题[1.8]
分类准确率：就是上面四、（一）[1.4.1]里面的损失函数是0-1损失时测试数据集上的准确率
在二类分类问题中，常用的评价指标是精确率与召回率。
以关注的类为正类，其他类为负类，4种情况出现的总数分别记作：
精确率和召回率都高时，F1值也会高。
书中举例的分类算法：k近邻法、感知机、朴素贝叶斯法、决策树、决策列表、逻辑斯谛回归模型、支持向量机、提升方法、贝叶斯网络、神经网络、Winnow等。
九、标注问题[1.9]
标注问题可以认为标注问题是分类问题的一个推广，标注问题又是更复杂的结构预测问题的简单形式。
评价标注模型的指标与评价分类模型的指标一样，常用的有标注准确率、精确率和召回率。
书中举例的标注算法：隐马尔可夫模型、条件随机场。
十、回归问题[1.10]
回归问题的学习等价于 函数拟合 ：选择一条函数曲线使其很好地 拟合已知数据 且很好地 预测未知数据 。
回归问题按照 输入变量的个数 ，分为一元回归和多元回归；
按照输入变量和输出变量之间关系的类型即 模型的类型 ，分为线性回归和非线性回归。
回归学习最常用的损失函数是 平方损失函数 ，在此情况下，回归问题可以由著名的 最小二乘法 求解。
第一章结束… …
链接：[ 全文章目录 ]