Multiple Objective Optimization in Recommender Systems 推荐系统多目标优化
ABSTRACT 摘要
We address the problem of optimizing recommender systems for multiple relevance objectives that are not necessarily aligned. Specifically, given a recommender system that optimizes for one aspect of relevance, semantic matching (as defined by any notion of similarity between source and target of recommendation; usually trained on CTR), we want to enhance the system with additional relevance signals that will increase the utility of the recommender system, but that may simultaneously sacrifice the quality of the semantic match. The issue is that semantic matching is only one relevance aspect of the utility function that drives the recommender system, albeit a significant aspect.
本论文讨论推荐系统中多个相关目标的优化问题,这些目标不一定一致。具体来说,给定一个推荐系统,该推荐系统针对相关性、语义匹配(定义为推荐源和目标之间的任何相似性概念;通常在CTR上进行训练)的一个方面进行优化,我们希望增加额外的相关信号来增强该系统,从而提高推荐系统的实用性,但这可能会牺牲语义匹配的质量。问题是语义匹配只是驱动推荐系统的效用功能的一个相关方面,尽管它是一个重要方面。
In talent recommendation systems, job posters want candidates who are a good match to the job posted, but also prefer those candidates to be open to new opportunities. Recommender systems that recommend discussion groups must ensure that the groups are relevant to the users’ interests, but also need to favor active groups over inactive ones. We refer to these additional relevance signals (job-seeking intent and group activity) as extraneous features, and they account for aspects of the utility function that are not captured by the semantic match (i.e. post-CTR down-stream utilities that reflect engagement: time spent reading, sharing, commenting, etc). We want to include these extraneous features into the recommendations, but we want to do so while satisfying the following requirements: 1) we do not want to drastically sacrifice the quality of the semantic match, and 2) we want to quantify exactly how the semantic match would be affected as we control the different aspects of the utility function. In this paper, we present an approach that satisfies these requirements.
在人才推荐系统中,招聘者希望应聘者与所发布的招聘启事相匹配,但也希望应聘者对新的机会敞开心扉。推荐讨论组的推荐系统必须确保讨论组与用户的兴趣相关,但也需要优先推荐活动组而不是非活动组。我们将这些额外的关联信号(求职意向和群体活动)称为无直接关系的特征,它们包含语义匹配未捕获的效用函数的各个方面(即反映参与度的点击后下游效用:花在阅读、分享、评论等上的时间)。我们希望在推荐中包含这些无直接关系的特征,但我们希望在满足以下要求的前提下,添加这些无关特征:1)我们不希望大幅牺牲语义匹配的质量,(2)我们希望量化当我们控制效用函数的不同方面时,语义匹配将如何受到影响。本文提出了一种满足这些要求的方法。
We frame our approach as a general constrained optimization problem and suggest ways in which it can be solved efficiently by drawing from recent research on optimizing non-smooth rank metrics for information retrieval. Our approach features the following characteristics: 1) it is model and feature agnostic, 2) it does not require additional labeled training data to be collected, and 3) it can be easily incorporated into an existing model as an additional stage in the computation pipeline. We validate our approach in a revenue-generating recommender system that ranks billions of candidate recommendations on a daily basis and show that a significant improvement in the utility of the recommender system can be achieved with an acceptable and predictable degradation in the semantic match quality of the recommendations.
我们将我们的方法框架为一个一般的约束优化问题,并从最近关于优化信息检索的非平滑排序度量的研究中提出了有效的解决方法。我们的方法具有以下特点:1)它是模型并且有不可知的特征,2)它不需要收集额外的标记训练数据,3)它可以很容易地作为计算中的附加阶段合并到现有模型中。我们在线上的推荐系统中验证了我们的方法,该系统每天对数十亿个候选推荐进行排序,并表明,在推荐的语义匹配质量下降可接受且可预测的情况下,推荐系统的实用性可以得到显著提高。
1. INTRODUCTION 简介
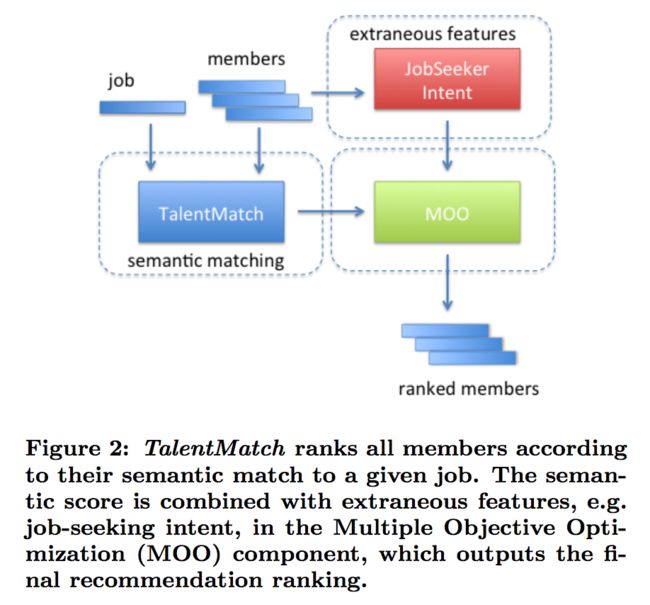
In designing recommender systems, we often have to balance multiple competing objectives. An example scenario can be drawn from a revenue-generating product at LinkedIn called TalentMatch, in which the recommender system, triggered by a job posted on the site, scours the entire member database to find the best candidates for the job. Those receiving the recommendations, job posters, want the candidates recommended to be a good fit for the job, but also prefer that the candidates be open to pursuing new opportunities. More specifically, a job poster would rather be recommended a candidate who is a great match for the job and also happens to be looking to change jobs, than the best match who happens to not be interested in exploring new opportunities. On the other hand, recommending a candidate who will certainly take the job if the offer was made, but who is not a good match for the job, will negatively affect the experience of the job poster. Therefore, given a ranking of candidates according to how well they match a given job and a ranking of candidates with regards to their job-seeking intent, the challenge is to combine both rankings into a final ranking that is optimal with regards to a given utility function.
在设计推荐系统时,我们常常需要平衡多个相互竞争的目标。以LinkedIn的TalentMatch产品为例,在该产品中,由发布在网站上的工作机会触发的推荐系统会搜索整个成员数据库,以找到该职位的最佳候选人。那些收到推荐的招聘者,希望被推荐的应聘者很适合这个职位,同时也更希望应聘者有寻找新机会的意愿。更具体地说,招聘者更愿意推荐系统给他推荐一个与职位非常匹配,而且碰巧也在找工作的候选人,而不是一个对寻找新机会不感兴趣的最佳人选。另一方面,推荐一位肯定会接受offer、但并不适合这个职位的候选人,这将对招聘者的体验产生负面影响。因此,根据候选人与给定职位的匹配程度对其进行排序,和根据其求职意向对候选人进行排序,挑战在于将这两个排序合并为最终排序,该排序对于给定的效用函数是最优的。
In most recommender systems, there is a utility function to be maximized: relevant engagement. In TalentMatch, relevant engagement is a multi-faceted objective: a) the job poster decides to purchase the set of candidate recommendations based on a snippet of information for each of the candidates (see Figure 1), b) the job poster decides to initiate communication with each of the recommended candidates in the purchased set, and c) each of the candidates contacted respond in a favorable fashion to the job poster.
在大多数推荐系统中,有一个效用函数需要最大化:相关参与。在TalentMatch中,相关的参与有多个目标:a)招聘者根据每个候选人的一小段信息购买候选人推荐集(见图1),b)招聘者开始与购买集中的每个推荐候选人进行沟通,以及c)每一位被联系的应聘者都对招聘者做出了回应。
In the TalentMatch system, the semantic model computes the probability that the feature vector representing the member and the feature vector representing the job are a good match. The model does this by computing similarities between subsets of the member’s feature vector and semantically related subsets of the job’s feature vector. The various similarities in this vector are then weighted by training against a given CTR metric using a supervised learning algorithm. We refer to the features used to generate the similarity vector as semantic features, a concrete example being the job description in the job posting and the job description of the member’s current position. In this case, the semantic features being compared are explicit, however, it may also be the case that the semantic features are latent (as in matrix factorization approaches to recommender systems). Extraneous features, on the other hand, exist only in the entity being recommended, not in the entity being recommended to. An example of an extraneous feature would be the job-seeking intent.
在TalentMatch系统中,语义模型计算代表成员的特征向量和代表职位的特征向量匹配的概率。该模型通过计算成员特征向量的子集和职位特征向量的语义相关子集之间的相似度来实现这一点。然后,利用监督学习算法,通过训练给定的CTR度量来加权该向量中的各种相似性。我们把用于生成相似向量的特征称为语义特征,一个具体的例子是职位发布中的职位描述和成员当前职位的职位描述。在这种情况下,被比较的语义特征是显式的,然而,语义特征也可能是潜在的(在推荐系统的矩阵分解方法中)。另一方面,无关特征只存在于被推荐的实体中,而不存在于推荐者(being recommended to)实体中。例如,求职意向是一个无关特征。
The job-seeking intent of each candidate is generated using another model, which for purposes of this paper, can be treated as a black-box that takes as input a candidate member and based on that member’s data (e.g. activity on the site and profile information), outputs a job-seeking propensity score and a probabilistic assignment to each of the job-seeking intent categories: active, passive, and non-job-seeker. Many members who do not self-identify as job-seekers on the site actually display job-seeking behavior and characteristics. Therefore, we can estimate job-seeking intent for every member of the site. Though only a proxy, job-seeking intent is a very good indicator of the likelihood with which a member contacted regarding a job opportunity will respond favorably (which is one of the aspects of the utility function in TalentMatch). The other two aspects of the utility function (purchase rate of candidate recommendations and likelihood that a job poster will communicate with the purchased recommendations) are accounted for by the semantic model. Intuitively, increasing the number of individuals with high job-seeking intent (those classified as active or passive) in the top-K recommendations, without drastically sacrificing the semantic match of the recommendations, should increase the utility of the TalentMatch recommender system by connecting job posters with candidates who will engage with them. Figure 2 gives a high-level overview of the relevant system components.
每个求职者的求职意向是使用另一个模型生成的,在本文中,该模型可以被视为一个黑盒,将一个求职者作为输入,并基于该求职者的数据(例如,网站上的活动和个人资料信息),输出求职意向分数和主动求职、被动求职、无意愿三种求职意愿的概率。很多在网站上没有自我认同为求职者的会员,实际上都表现出了求职行为和特点。因此,我们可以估计每个成员的求职意愿。尽管只是一个中间桥梁,求职意向是一个非常好的指标,表明与某个工作机会有关的成员可能作出反应的可能性(这是TalentMatch中效用函数的一个方面)。效用函数的另外两个方面(候选推荐的购买率,和招聘者与购买的候选人进行联系的可能性)由语义模型进行说明。直观地说,在top-K推荐中增加具有高度求职意向的个人(被归类为主动或被动的)的数量,而不大幅牺牲推荐的语义匹配度,通过连通招聘者和会响应招聘的应聘者提升了TalentMatch推荐系统的效用。图2给出了相关系统组件的简要概述。
Compounding the issue of multi-faceted objectives is the fact that in live production systems, models often need to evolve in a progressive fashion: the model may have initially optimized for only one aspect of relevant engagement (e.g. purchase rate of candidate recommendations) and it would be preferable to improve the model incrementally (as soon as a new feature like job seeking intent becomes available), rather than waiting for a complete redesign and development lifecycle of a new model. The incrementally improved model then bridges the old and the new models, and allows for additional analysis on the performance of the new feature, which may in turn influence how it is incorporated in the new model.
在实际生产系统中,模型通常需要以渐进的方式发展:模型最初可能只针对相关参与的一个方面(例如候选推荐的购买率)进行了优化,并且会逐步改进模型(一旦出现求职意向等新功能),而不是重新设计和开发一个全新的模型。逐步改进的模型合并了新旧模型,并对新特性的性能进行额外的分析,而新特性又可能影响如何将其合并到新模型中。
In this paper we describe a general approach for incorporating extraneous features into a semantic model, which result in the need to optimize for objectives which are not necessarily aligned. More specifically, given a model which outputs recommendations ranked according to some notion of semantic relevance, we want to add certain features which contribute to the overall utility of the users of the recommender system, but that may negatively affect the semantic relevance of the recommendations. This approach is model and feature agnostic, does not require additional labeled training data to be collected, and can be easily incorporated into an existing model as an additional stage in the computation pipeline. We validate our approach by A/B testing it on TalentMatch system, which currently ranks billions of job-member pairs on a daily basis, and show that a significant improvement in the utility of the recommender system (42% increase on email reply rate) can be achieved with an acceptable and predictable degradation in the original relevance of the recommendations.
在本文中,我们描述了一种将无关特征合并到语义模型中的通用方法,这种方法可以对不一定一致的目标进行优化。更具体地说,给定一个根据语义相关性进行推荐的模型,我们希望添加一些有助于推荐系统用户整体效用的特性,但这可能会对推荐的语义相关性产生负面影响。这种方法不依赖于模型和特征,不需要收集额外的标记训练数据,并且可以很容易地作为计算中的附加阶段合并到现有模型中。我们在每天对数十亿个 职位-候选人 对进行排序的TalentMatch系统上进行了A/B测试,验证了我们的方法,该方法显著提升了推荐系统的实用性(电子邮件回复率提高了42%),同时推荐的原始相关性的下降可接受和可预测。
2. PROBLEM FORMULATION 问题表述
In this section we discuss a general template for framing the kinds of problems we are targeting in this paper and in Section 4.1 we discuss the instantiation of this general template for the specific TalentMatch scenario.
We start with a model which is optimized for semantic relevance. We then want to enhance this model with additional features which will increase the utility of the recommender system, but at a potential loss in the semantic relevance of the recommendations. Adding these additional features to the model will result in an enhanced model with additional objectives to be optimized. These additional objectives will be optimized conditionally on the semantic relevance objective having already been optimized.
在本节中,我们将讨论一个通用模板,用于构建本文所针对的各种问题;在第4.1节中,我们将讨论该通用模板在TalentMatch场景中的应用。
我们从一个以语义相关性为优化目标的模型开始。然后,我们希望添加额外的特性来提升这个模型,以增加推荐系统的实用性,但是在推荐的语义相关性方面可能会有损失。添加这些附加的特性,会提升模型,同时会增加额外的优化目标。这些附加的目标将在语义相关目标已经优化的基础上有条件地优化。
2.1 Adding a single competing objective 增加单一竞争目标
In the simplest case, we would have only one feature to add to the semantic model, which equates to one additional objective to be increased (adding more features that map to only one additional objective can be handled similarly). We also want to penalize enhanced models in a manner that is correlated with the distance between the semantic relevance score distribution of the items in the top-K ranking as output by the semantic model, and the semantic relevance score distribution of the items in the top-K ranking as output by the enhanced model (note that the enhanced model outputs a ranking based on the enhanced scores, but we need to map those scores back to their semantic counterparts to compare the two distributions). These requirements are expressed by the following loss function:
![]() (1)
(1)
where
- X is the single feature to be added, a matrix of dimensions m×n;
- m is the number of targets of the recommender system;
- n is the number of recommendations per target;
- Y represents semantic relevance scores, also a matrix of dimensions m × n;
- w is the parameter associated with the feature to be added;
- f is the enhanced model which perturbs the semantic relevance score Y according to the new feature X and parameter w;
- g is an objective to be maximized which contributes the overall utility of the recommender system but is not accounted for in the semantic model;
- ∆ is a non-negative measure which is indicative of the distance between the semantic match score distribution and the enhanced score distribution;
- π is a function which returns a top-K ranking, and n >> K;
- λ is a positive trade-off parameter.
Alternatively, it may be easier to visualize the objective as a constrained optimization problem where we have a limit on how much we are allowed to deviate from the top-K score distribution based on the semantic model:
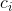 is the ith constraint on the top-K distribution distance between the semantic match score distribution and the enhanced score distribution;
is the ith constraint on the top-K distribution distance between the semantic match score distribution and the enhanced score distribution;- l is the number of constraints on the semantic score distribution deviation.
Given the constrained optimization perspective, in the simple case where l = 1 we could analyze how g trends as a function of various values for c, from which we could extract the Pareto frontier [6] and which we could use to make a data-driven decision on what value of c is appropriate. Note that if, in the Pareto frontier, g turns out to be a linear function of c, then the slope of the line would be the value of the λ parameter in Equation 1.
在最简单的情况下,我们将只有一个特性要添加到语义模型中,这相当于要增加一个附加目标(添加更多映射到一个附加目标的特性可以类似地处理)。我们还希望对增强模型进行惩罚,惩罚方式与语义模型输出的top-K排序中item的语义相关性得分分布和增强模型输出的top-K排序中item的语义相关性得分分布之间的距离相关(注意,增强模型输出基于增强分数的排序,但我们需要将这些分数映射回它们的语义对应项以比较这两个分布)。这些需求由以下损失函数表示:
![]() (1)
(1)
其中:
- X是要添加的单个特征,一个尺寸为m×n的矩阵;
- m是推荐系统的目标数;
- n是每个目标的推荐个数;
- Y表示语义相关性得分,也是m×n的矩阵;
- w是与要添加的特征相关联的参数;
- f是根据新特征X和参数w扰动语义关联度Y的增强模型;
- g是最大化的目标,它有助于推荐系统的总体效用,但在语义模型中没有考虑到;
- ∆是一个非负的度量,表示语义匹配分数分布和增强分数分布之间的距离;
- π是一个返回top-K排名的函数,n>>K;
- λ是一个正的权衡参数。
也可以将目标视为一个约束优化问题,对允许偏离基于语义模型的top-K分数分布的程度进行限制:
其中:
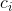 是语义匹配分数分布和增强分数分布之间top-K分布距离的第i个约束条件;
是语义匹配分数分布和增强分数分布之间top-K分布距离的第i个约束条件;- l是语义得分分布偏差的约束个数。
考虑到约束优化的观点,在l=1的简单情况下,我们可以分析g的趋势如何作为c的各种值的函数,从中我们可以提取帕累托前沿[6],我们可以基于数据,确定c的哪个值是合适的。注意,如果在Pareto前沿,g是c的线性函数,那么直线的斜率就是方程1中λ参数的值。
2.2 Adding multiple competing objectives 添加多个竞争目标
In the case where the additional features with which we will enhance the semantic model lead to multiple additional objectives, we have the following general version of the problem:
- G is the set of additional objectives to be maximized {
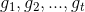 };
}; - t is the number of additional objectives to be maximized;
- X are the features to be added, a matrix of dimensions m×n×p;
- p is the number of features being added;
- w is the parameter vector associated with the features to be added with dimension 1 × p;
- F is the enhanced model which perturbs the semantic match score Y according to the new features X and parameter w.
如果我们添加的特性导致模型添加多个目标,则有如下优化问题:
- G是要最大化的附加目标集合 {
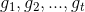 };
}; - t是要最大化的附加目标数;
- X是要添加的特征,是m×n×p的矩阵;
- p是要添加的特征数;
- w是与添加特征相关的参数向量,是1 × p的矩阵;
- F是根据新特征X和参数w扰动语义匹配得分Y的增强模型。
3. COMPUTATIONAL STRATEGY 计算策略
The functions g and ∆ described in Section 2 are non-smooth since they depend on a ranking which in turn depends on a sort operation. Therefore, traditional optimization approaches which leverage the gradient of a function are not directly applicable.
In very small parameter spaces (one or two parameters), grid (exhaustive) search is an acceptable and very simple to implement computational strategy. For larger parameter spaces, we can devise smoothed approximations to g and ∆ that are amenable to traditional gradient-based methods and therefore able to handle parameter spaces where grid search would be unfeasible. In this Section we discuss using such approximations in our problem formulation and in Section 4.2 we discuss the computational strategy followed in the TalentMatch case study.
第2节中描述的函数g和∆是非平滑的,因为它们依赖于排序,而排序依赖sort操作。因此,传统的利用函数梯度的优化方法并不直接适用。
在非常小的参数空间(一个或两个参数)中,网格(穷举)搜索是一种可接受的且非常易于实现的计算策略。对于更大的参数空间,我们可以设计对g和∆的平滑逼近,这是对传统的基于梯度的方法的改进,因此能够处理网格搜索不可行的参数空间。在这一节中,我们讨论如何在我们的问题公式中使用这种近似,在第4.2节中,我们讨论在TalentMatch中遵循的计算策略。
Recent research on “learning to rank” for information retrieval addresses the need to optimize non-smooth rank-based metrics. There are two approaches that are particularly interesting in this direction: SoftRank [9] and SmoothRank [3]. These approaches develop smooth approximations to IR metrics such as the Normalized Discounted Cumulative Gain (NDCG) and the Average Precision (AP). We can formulate our g and ∆ functions so that they have a similar form to those IR metrics and then we can employ the techniques described in [9, 3] for optimizing them.
For example, we can consider the original semantic relevance score from the TalentMatch model to be the ground-truth measure of relevance of each candidate member given a job. In an IR setting, we would have queries and documents, where documents have a measure of relevance to a particular query. In the TalentMatch model, a job is equivalent to a query and a candidate member is equivalent to a document.
最近关于信息检索“学习排序”的研究指出优化非平滑排序度量的必要。在这个方向上有两种方法特别有趣:SoftRank[9]和SmoothRank[3]。这些方法发展了对IR指标的平滑近似,如归一化折损累计增益(NDCG)和平均精度(AP)。我们可以定义g和∆函数,使它们具有与IR度量相似的形式,然后我们可以使用[9,3]中描述的技术来优化它们。
例如,我们可以将TalentMatch模型中的原始语义相关性分数作为每个候选成员和职位相关性的基本真实度量。在IR设置中,我们有查询和文档,其中文档与特定查询有一定的相关性。在TalentMatch模型中,职位等同于查询,候选成员等同于文档。
One possible instantiation of g and ∆ would be as follows: assume we do not wish to distinguish between active and passive candidates; we would then have a binary notion of relevance for a given candidate, {job-seeker = 1, non-job- seeker = 0} that we want to maximize in the top-K results. This is a good match for the AP measure. We then need a constraint function which penalizes how much deviation there is from the original relevance-based ranking. It turns out that an adapted form of the NDCG measure would be appropriate here.
g和∆的一个可能的实例如下:假设我们不想区分主动和被动的候选人;对一个候选人,我们可以定义一个二元表示,{job seeker=1,non job-seeker=0},我们希望在top-K结果中最大化这个二元表示。我们将这个二元表示作为AP度量。然后我们需要一个约束函数来惩罚与原始的基于相关性的排序有多大的偏差。结果表明,采用基于NDCG度量的某种变换形式比较合适。
This leaves us with the following smooth approximation to our objective function, using the approximation in equation 9 from [3]:
where:
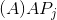 is the Approximate Average Precision for a given job j;
is the Approximate Average Precision for a given job j;- f is the enhanced model which perturbs the semantic match score, originally defined in Equation 1;
- σ is the smoothing parameter as described in [3];
- n is the number of recommendations per job j;
 is the label of the ith recommended candidate, either job-seeker = 1 or non-job-seeker = 1;
is the label of the ith recommended candidate, either job-seeker = 1 or non-job-seeker = 1;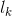 is the label of the recommended candidate at rank k, either job-seeker = 1 or non-job-seeker = 1;
is the label of the recommended candidate at rank k, either job-seeker = 1 or non-job-seeker = 1;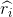 is the smooth rank, as defined in equation 5 in [3].
is the smooth rank, as defined in equation 5 in [3].
这样,我们就可以使用[3]中方程9的近似,对目标函数进行以下平滑近似:
其中:
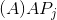 是给定职位j的近似平均精度;
是给定职位j的近似平均精度;- f 是等式1中定义的扰动语义匹配分数的增强模型;
- σ [3]中所述的平滑参数;
- n 是每个职位j的推荐个数;
 是第i个推荐候选人的标签,either job-seeker = 1 or non-job-seeker = 1;
是第i个推荐候选人的标签,either job-seeker = 1 or non-job-seeker = 1;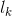 是排序为k的推荐候选人的标签,either job-seeker = 1 or non-job-seeker = 1;
是排序为k的推荐候选人的标签,either job-seeker = 1 or non-job-seeker = 1;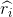 是平滑排序,如[3]中等式5所定义。
是平滑排序,如[3]中等式5所定义。
And the following smooth approximation to our constraint function, using the approximation from equation 8 in [3]:
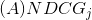 is the Approximate Normalized Discounted Cumulative Gain for a given job j;
is the Approximate Normalized Discounted Cumulative Gain for a given job j;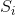 is the semantic score for the ith candidate, obtained from using the TalentMatch model;
is the semantic score for the ith candidate, obtained from using the TalentMatch model;- n is the number of recommendations per job j;
- D(k) is the discounting associated with ranking k, which could be defined as
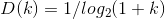 ;
; 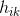 is defined in equation 7 in [3] to be a soft version of an indicator variable that indicates the probability that the
is defined in equation 7 in [3] to be a soft version of an indicator variable that indicates the probability that the 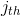 recommendation is ranked at the
recommendation is ranked at the 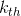 position.
position.
f, which is the enhanced model that perturbs the semantic match score, originally defined in Equation 1, enters Equation 5 through ![]() :
:
Where d(k) is the index of the recommendation which was ranked at position k by f .
下面是约束函数的平滑近似,使用了[3]中等式8的近似:
其中:
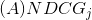 是给定职位的近似归一化折损累计增益;
是给定职位的近似归一化折损累计增益;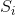 是第i个候选人的语义得分,得分由TalentMatch模型给出
是第i个候选人的语义得分,得分由TalentMatch模型给出- n是每个职位j的推荐个数;
- D(k)是排序k的折扣,可定义为
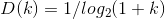 ;
;  在[3]等式7中定义,表示第j个推荐人在第k个位置的概率。
在[3]等式7中定义,表示第j个推荐人在第k个位置的概率。
f是扰动语义匹配分数的增强模型,最初定义在等式1中,通过![]() 引入等式5:
引入等式5:
式中,d(k)是在位置k处按f排名的推荐index。
There are many other ways to formulate our approach using these smoothed approximations. For example, if instead of the job-seeking categories (active, passive, and non-job-seeker) we wished to use the job-seeking intent score, we could formulate g using (A)NDCG instead of (A)AP. Additionally, if the functional form of f in equation 1 is such that a parameter vector w of 0 in the enhanced model yields the equivalent of the semantic model, an Euclidean norm constraint on w could be used instead of (A)NDCG for the ∆ function.
有很多其他的方法来使用这些平滑的近似来表示我们提出的方法。例如,如果我们希望使用求职意向得分而不是求职类别(主动、被动和非求职者),我们可以使用(A)NDCG而不是(A)AP来表示g。此外,如果方程1中f的函数形式使得增强模型中的参数向量w为0产生与语义模型等效的结果,则可以使用对w的欧几里德范数约束,而不是(a)NDCG作为∆函数。
4. TALENT MATCH CASE STUDY 人才匹配案例研究
We illustrate our approach with the TalentMatch system, where given a job posted on the site, we generate a ranked list of candidates with regards to how well the candidates match the job. This semantic model outputs the probability that the candidate is a good match to the job. We want to enhance this model with the job-seeking intent of the candidate so that the candidates being recommended are both good matches for the job, as well as open to new job opportunities. Our hypothesis is that this will contribute to increased engagement between the job poster and the recommended candidates.
我们用TalentMatch系统来说明我们的方法,在该系统中,给定一个发布在网站上的职位,我们就候选人与职位匹配的程度生成一个候选人的排序列表。该语义模型输出候选对象与职位匹配的概率。我们希望根据求职者的求职意向来改进这一模式,使被推荐的求职者既能匹配职位,又有换工作的意愿。我们的假设是,这将有助于增加招聘者和推荐候选人之间的接触。
There are many ways to incorporate the job-seeking intent signal into the TalentMatch model. As discussed in section 1, the job-seeking intent model outputs, for each member, a job-seeking propensity score and a probabilistic assignment to each of the job-seeking intent categories: active, passive, and non-job-seeker. Our objective is to increase the average number of active and passive candidates in the top-K recommendations. We want to achieve this objective by perturbing slightly the semantic ranking so that if there is a candidate Cx with a semantic score of 0.9 in rank 1 who has a low job-seeking intent (classified as a non-job-seeker), and another candidate, Cy, in rank 2 with a match score of 0.88, but that happens to have a high job-seeking intent (classified as active or passive), then we would like to bump Cy up to rank 1 and bump Cx down to rank 2. We do not necessarily want to eliminate Cx from the final ranking, nor do we want to excessively bump the candidate down the ranking. More importantly, we want a systematic way to perform this re-ranking perturbation.
有很多方法可以将求职意向信号纳入TalentMatch模型。如第1节所述,求职意向模型为每个成员输出一个求职倾向得分和主动求职、被动求职、无求职意愿的概率。我们的目标是在top-K推荐中增加主动和被动求职候选人的平均数量。我们希望通过稍微扰动语义排序来实现这一目标,如果排序为1的候选人为Cx,其语义得分为0.9,但是求职意向较低(分类为非求职者),而排序为2的候选人为Cy,其语义得分为0.88,但有较高的求职意向(分类为主动或被动),我们希望将Cy提升到第一位,将Cx下降到第二位。我们不一定想在最终排名中淘汰Cx,也不想过分地把Cx从排序中挤下来。更重要的是,我们需要一种系统的方法来执行这种重新排序的扰动。
A simple strategy would be to remove from the ranked list based on semantic matching scores all those recommended candidates with a job-seeking intent score below a certain threshold t, backfilling if needed to make sure we have K recommendations (we discuss below how this specific heuristic is a special case of our suggested approach). This approach still requires us to estimate the threshold t, but more crucially, it also incurs the risk of completely eliminating high-quality matches from the final ranking, an outcome we do not want.
一个简单的策略是根据语义匹配分数从排名列表中删除所有那些求职意向分数低于某个阈值t的推荐候选人,如果需要,进行填充以确保我们有K个推荐(下面我们将讨论这种特定的启发式方法是我们推荐方法的一个特例)。这种方法仍然需要我们估计阈值t,但更关键的是,它也会带来从最终排名中完全淘汰高质量匹配度的风险,这是我们不希望看到的结果。
4.1 TalentMatch Problem Formulation TalentMatch问题公式
In order to come up with a strategy for re-ranking that satisfies our requirements, we frame our problem using the template described in section 2. The average number of active and passive candidates in the top-K recommendations is actually an instance of a familiar metric: mean precision at K, where our binary relevance measure is an indicator function that returns 1 if the member is active or passive and 0 otherwise, ![]() ∈ {0, 1}. For a given job posted to the site, precision at K is:
∈ {0, 1}. For a given job posted to the site, precision at K is:
Where 1{A} is the indicator function applied to A, and 1{A} = 1 is A is true and 0 otherwise, r(i) is the ranking of the ![]() candidate, and n is the number of candidates in the result set. Our objective to be maximized, the mean precision at K, which maps to the g function in equations 1 and 2 is:
candidate, and n is the number of candidates in the result set. Our objective to be maximized, the mean precision at K, which maps to the g function in equations 1 and 2 is:
为了提出一个重新排序的策略来满足我们的需求,我们使用第2节中描述的模板来构建我们的问题。top-K推荐中的主动和被动候选的平均数实际上是一个常见度量的实例:K的平均精度,其中我们的二元相关性度量是一个指标函数,如果成员是主动或被动的,则返回1,否则返回0,li∈{0,1}。对于发布到站点的给定职位,K的精度为:
其中1{A}是A的指示符函数,如果A为true,则1{A}=1,否则为0。r(i)是第i个候选的排名,n是结果集中的候选数。我们的目标是最大化,K处的平均精度,它映射到等式1和2中的g函数是:
The functional form of f, the enhanced model in equations 1 and 2, can also be specified in a variety of ways. One possible option is to use a a linear combination of the TalentMatch semantic and job-seeking intent scores. This would not be ideal: we want both, good matches and likely to be job-seeking candidates; therefore, a multiplicative feature interaction is what we seek. We settled on the following formulation:
![]() (9)
(9)
This is equivalent to applying a small boost to the semantic match score (y), and allowing for the boost to be different for actives (α) and passive (β) candidates. Solving the optimization problem defined in equations 1 and 2, with the specific functional forms defined here will yield appropriate values for α and β.
f的函数形式,即方程1和方程2中的增强模型,也可以用多种方式指定。一种可能的选择是使用TalentMatch语义和求职意向分数的线性组合。这并不理想:我们想要两者都是,好的匹配,而且很可能是求职者;因此,我们寻求的是一个乘法特征交互。我们决定采用以下公式:
![]() (9)
(9)
这相当于对语义匹配分数(y)应用一个小的提升(boost),并允许主动(α)和被动(β)候选的提升是不同的。用这里定义的特定函数形式求解方程1和2中定义的优化问题,将得到α和β的适当值。
Given our chosen functional for f, it can be seen that the simple heuristic suggested earlier is actually a special case in our approach, where α and/or β are set to large enough values so as to effectively rank all members with a job-seeking intent score above the threshold t over those members with a score below t. Section 5 discusses how this strategy is suboptimal (it causes an unacceptable loss in semantic relevance).
Finally, we need to specify how we will measure the deviation of the enhanced model distribution from the semantic model distribution, that is, the functional form for ∆ in equations 1 and 2. There are various histogram distance functions to choose from [2], examples of which include Euclidean distance and Kullback-Leibler divergence. We settled on using the Euclidean distance between the two histograms, or more specifically, the sum of squared errors of the histogram buckets, each histogram having b buckets:
Where ![]() is the histogram of semantic match scores of the top-K candidates ranked by the semantic match score and
is the histogram of semantic match scores of the top-K candidates ranked by the semantic match score and ![]() is the histogram of semantic match scores of the top-K candidates ranked by the enhanced score.
is the histogram of semantic match scores of the top-K candidates ranked by the enhanced score.
考虑到我们为f选择的函数,可以看出前面建议的简单启发式方法实际上是我们方法中的一个特例,其中α和/或β被设置为足够大的值,以便有效地将所有求职意向得分高于阈值t的成员排在得分低于阈值t的成员之上。第5节讨论了这一点策略是次优的(它会导致不可接受的语义相关性损失)。
最后,我们需要具体说明如何测量增强模型分布与语义模型分布之间的偏差,即等式1和2中∆的函数形式。[2]中有各种各样的直方图距离函数可供选择,其中包括欧几里德距离和Kullback-Leibler散度。我们决定使用两个直方图之间的欧几里德距离,或者更具体地说,直方图桶的平方误差之和,每个直方图都有b个桶:
其中![]() 是按语义匹配得分排序的前K个候选的语义匹配得分直方图,
是按语义匹配得分排序的前K个候选的语义匹配得分直方图,![]() 是按增强得分排序的前K个候选的语义匹配得分直方图。
是按增强得分排序的前K个候选的语义匹配得分直方图。
4.2 TalentMatch Computational Strategy TalentMatch计算策略
Since we only have two parameters: α and β, and given our intuition that the optimal parameters will probably lie in the interval [1.0, 2.0], a grid search turns out to be an acceptable computational strategy in this scenario. We break up the grid search into 2 runs: a coarse run (to see what region of the search space we should focus on) and a fine run (to zero in on the desired values). In each run we generate all the plans to be tested (a plan being an assignment of values to α and β) and evaluate our g and ∆ functions for each plan generated.
由于我们只有两个参数:α和β,并且根据我们的直觉,最优参数可能位于区间[1.0,2.0],在这种情况下,网格搜索是一种可接受的计算策略。我们将网格搜索分为两个运行:粗略运行(以确定我们应该关注搜索空间的哪个区域)和精细运行(以关注期望得到的值)。在每次运行中,我们生成所有要测试的计划(计划是对α和β值的赋值),并对生成的每个计划的g和∆函数进行评估。
5. EVALUATION AND RESULTS 评估和结果
For estimating the α and β parameters to be used in Equation 9, we created a sample dataset of jobs recently posted to the site and computed a maximum of 9000 recommendations for those jobs using the TalentMatch model. We filtered all recommendations with a threshold of 0.6 on the TalentMatch semantic score, and then removed all jobs which did not have at least 6 recommendations (we do not show results on the site unless there are at least 6 relevant matches and we include only the top-24 candidates in the recommendation set). This left us with a total of 760 jobs, each with anywhere from 6 recommendations to 9000 recommendations. We then generated the plans as per Section 4.2 and evaluated our g and ∆ functions.
Our g function is the mean precision at K, as defined in Equation 8, where K = 12 since that is how many snippets of candidate recommendations we show in a single page.
Also, for the measure of divergence, our ∆ function, we compared the distribution of the minimum score of the top-12 ranking, given that we want to ensure relevant recommendations in the worst case on the first results page.
为了估计方程式9中使用的α和β参数,我们创建了一个最近发布到站点的职位样本数据集,并使用TalentMatch模型计算了这些职位的最多9000条推荐。我们筛选了TalentMatch语义评分阈值为0.6的所有推荐,然后删除了所有没有至少6个推荐的职位(除非至少有6个相关匹配,否则我们不会在网站上显示结果,并且我们只在推荐集中包含前24名候选人)。这给我们留下了760个工作岗位,每个岗位都有6到9000条推荐。然后,我们根据第4.2节生成了计划,并评估了我们的g和∆函数。
我们的g函数是K的平均精度,如等式8所定义,其中K=12,因为这是我们在一个页面中显示的候选推荐片段的数量。
此外,对于差异的度量,我们的∆函数,我们比较了前12名的最低得分分布,因为我们希望在最坏的情况下,在第一个结果页上确保相关的建议。

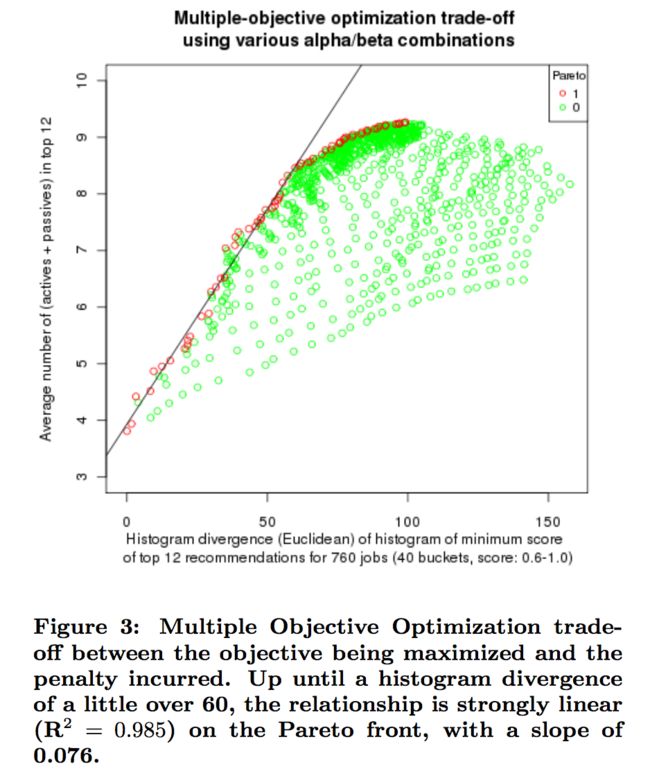
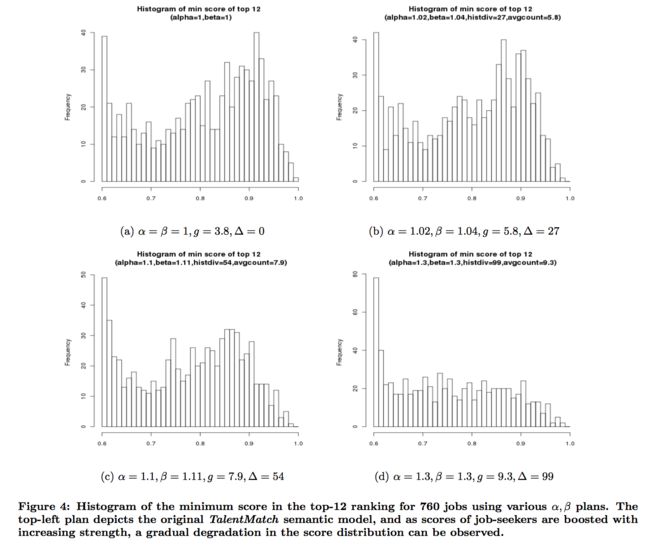
Figure 3 shows the result of the fine grid search run, which illustrates the risk-reward trade-off in our experiment: up until a histogram divergence of a little over 60, we pay a penalty that is linear with regards to the increase in the average number of active and passive members in the top-12 result set. Table 1 shows a few of the points used in the plot, including the original plan (equivalent to setting α and β to 1.0), which also indicates the average number of active and passive candidates in the top-12 result set of the original plan to be nearly 4. Figure 3 tells us that we can double that number if we are willing to pay a penalty of about 64 in the histogram divergence, and also tells us what to set α and β to: 1.15 (see table 1). Figures 4(a)-4(d) give an idea of how good/bad a histogram divergence of 64 is. For reference, as per table 1, setting α to 1.3 and α to 1.0 causes an unacceptable loss in relevance (the histogram divergence is too high and the gain in the objective does not justify it).
图3显示了精细网格搜索运行的结果,它说明了我们实验中的风险-回报权衡:直到直方图差异略大于60,我们支付的惩罚与前12个结果集中的主动和被动成员平均数量的增加成线性关系。表1显示了该图中使用的一些点,包括原始计划(相当于将α和β设置为1.0),这也表明原始计划前12个结果集中的主动和被动候选的平均数接近4。图3告诉我们,如果我们愿意支付柱状图散度约64的惩罚,我们可以将这个数字翻一番,还告诉我们将α和β设置为:1.15(见表1)。图4(a)-4(d)给出了64的直方图散度的好坏。作为参考,如表1所示,将α设置为1.3和α1.0会导致不可接受的相关性损失(直方图发散度太高,目标中的增益不能证明这一点)。
All of the plans on the Pareto front in figure 3 have similar coefficients for α and β, which is tied to the fact that the goal we are trying to maximize is the combined number of active/passive candidates in the top-12, and presumably the values for the weights would diverge more had we favored one category or the other. These results point to reasonable strategies that should be evaluated using A/B testing: a plan where α = β = 1.07 and a plan where α = β = 1.15. A/B testing turns out to be a crucial component to the methodology described in this paper. Our approach provides the tools for generating reasonable values for α and β: no matter what the desired risk-reward trade-off of a specific application, only plans in the Pareto frontier should be chosen. However, our choice for what is an acceptable histogram divergence will only be meaningful if once in production, the rate with which job posters purchase candidate set recommendations and the rate with which job posters contact the purchased recommended candidates does not decrease substantially.
图3中帕累托边界的所有计划对于α和β都有相似的系数,这与我们试图最大化的目标是前12名中的主动/被动候选组合的数量有关,如果我们倾向于一个类别或另一个类别,权重的值可能会出现更大的差异。这些结果指出了应使用A/B测试评估的合理策略:α=β=1.07的计划和α=β=1.15的计划。A/B测试是本文所述方法的关键组成部分。我们的方法提供了为α和β生成合理值的工具:无论特定应用的期望风险回报权衡是什么样的,只应选择帕累托边界的计划。然而,我们对于什么是可接受的直方图差异的选择只有在以下情况下才有意义:一旦应用到线上,招聘者购买候选人集推荐的比率和招聘者与购买的推荐候选人联系的比率没有大幅度下降。
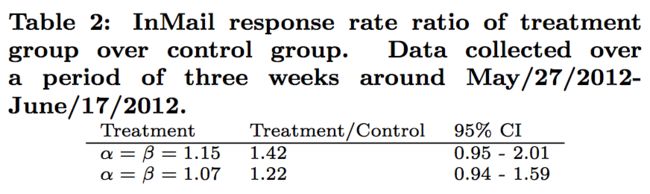
As mentioned in Section 1, we would like to increase the likelihood of relevant engagement for TalentMatch. If the job-seeking intent is to be of any use to us, we would expect the rate of replies to InMails (LinkedIn e-mails) from job posters about job opportunities to be higher for members with high job-seeking intent. We determined that members classified as having a high job-seeking intent (actives/passives) are 16× more likely to reply to an InMail regarding a career opportunity, with a 95% confidence interval of 15-17x (intervals computed by the method of E. C. Fieller [4]). These numbers are based on InMail activity that took place over a period of 10 days, during which time the number of non-job-seekers contacted was nearly the same as the number of actives/passives contacted.
如第1节所述,我们希望增加招聘者/求职者与TalentMatch的互动。如果求职意向对我们有用,我们预计求职意向高的会员会对招聘者发布职位的InMail有更高的回复率。被归类为具有高度求职意向(主动/被动)的成员,在职业机会方面,向InMail回复的可能性要高出16倍,95%的置信区间为15-17倍(区间由E.C.Fieller[4]方法计算)。这些数字是根据在10天内的InMail行为得出的,在此期间,与非求职者接触的人数几乎与主动/被动接触的人数相同。
Assuming that all members in the top-12 ranking are contacted about the job opportunity, our results suggest that we can double the desired relevant engagement. Given that the probability of positively replying for non-job-seekers is pn(reply) = 0.028, and the probability of replying for actives/passives is pa/p(reply) = 0.45 (as computed using the 10-day sample), and given that our analysis shows that we can double the average number of actives/passives in the top-12 from 4 to 8 at an acceptable relevance loss, we expect to double the expected relevant engagement: 0.028 × 8 + 0.45 × 4 ≈ 2 versus 0.028 × 4 + 0.45 × 8 ≈ 4.
假设就工作机会联系排名前12位的所有候选人,则期望的相关参与度会翻一番。假设非求职者的正面回复概率为![]() ,主动/被动回复概率为
,主动/被动回复概率为![]() (使用10天样本计算),由于在可接受的相关性损失下,我们可以将前12名中的主动/被动的平均数量从4倍增加到8倍,我们期望预期的相关参与会增加一倍:0.028×8+0.45×4≈2与0.028×4+0.45×8≈4。
(使用10天样本计算),由于在可接受的相关性损失下,我们可以将前12名中的主动/被动的平均数量从4倍增加到8倍,我们期望预期的相关参与会增加一倍:0.028×8+0.45×4≈2与0.028×4+0.45×8≈4。
We deployed the A/B test experiment and let it run for a couple of weeks before we started collecting data for analysis (until the “novelty effect” often caused by a new feature being deployed live had subsided). To measure the change in InMail reply rate, we looked at all emails created in a period of three weeks and observed how many were replied to. Table 2 shows the increase in response rate for each A/B test treatment bucket along with their confidence intervals. The actual increase follows the expected linear relationship as expected from the Pareto frontier, and though there is high variance, the 95% confidence intervals contain the expected values.
我们进行了A/B实验,在开始收集数据进行分析之前让它运行几个星期(直到经常由实时部署的新功能引起的“新奇效应”消退)。为了衡量InMail回复率的变化,我们查看了三周内创建的所有电子邮件,并观察了有多少邮件被回复。表2显示了每个A/B试验处理桶的回复率及其置信区间。实际增长遵循帕累托前沿的预期线性关系,尽管存在高方差,但95%置信区间包含预期值。
We now turn our attention to the effect of the re-ranking perturbation on the booking rate. More specifically, we want to quantify the effect of the histogram divergence. For this, during the same time period, we looked at the booking rate in each of A/B test buckets. Table 3 summarizes our findings. It shows a slight degradation in booking rate for the most extreme treatment bucket. However, looking at the rate with which job posters email candidates in the purchased set (InMails per booking) shows a different story.
我们现在将注意力转移到重新排序扰动对预订率的影响上。更具体地说,我们想量化直方图散度的影响。为此,在同一时间段内,我们查看了每个A/B测试桶中的预订率。我们的发现如表3。从表3可看出,最极端处理桶的预订率略有下降。然而,招聘者给应聘者发邮件的比率(每个预定的InMails)却不是这种情况。
Table 4 shows that on average, job posters choose to email candidates more often in the treatment group than in the control group. This is evidence that job posters do not email all candidates in the purchased set, but rather pick and choose who they will contact. This fact explains why the actual average increase in InMail response rate was not as high as expected: we had assumed that job posters contact all of the candidates in the result set, but this turns out not to be the case. The control group shows that job posters only contact an average of approximately 2 members from the purchased candidate result set. More importantly, since job posters do not have access to the job-seeking intent of each candidate (nor to most of the information we use to determine job-seeking intent, such as job searches), there must be something else in the candidate’s profile which compels job posters to email candidates we’ve identified as job-seekers more often than those we have not. Perhaps job-seeking candidates have more complete or more curated profiles. Nevertheless, this means that the snippet we show job posters, based on which they make the decision of whether or not to purchase, is not well representative of the value of the candidate result set. This finding is something that we plan on exploring further, as it suggests that, given the right snippet (one which better conveys the value of the candidate result set to the job poster), the booking rate for the treatment groups should be higher than for the control group.
表4显示,平均来说,与对照组相比,实验组的招聘者选择给应聘者发送电子邮件的频率更高。这就证明了招聘者并不是给购买的所有候选人发送电子邮件,而是只给他们想联系的候选人发送邮件。这一事实解释了为什么实际平均增加的InMails回复率没有预期的那么高:我们假设招聘者会联系结果集中的所有候选人,但事实并非如此。对照组显示,招聘者平均只与购买的候选结果集中的大约2名成员联系。更重要的是,由于招聘者无法获取每位应聘者的求职意向(也无法获取我们用来确定求职意向的大部分信息,如求职信息),在求职者的个人资料中,肯定还有其他一些东西使招聘者向我们确定为求职者的候选人发送电子邮件,而不是那些非求职者。也许求职者有更完整或更详细的个人资料。尽管如此,这意味着我们给招聘者展示的片段并不能很好地代表候选人结果集的价值,而这些片段是他们决定是否购买的依据。这一发现是我们计划进一步探索的,因为它表明,在给定正确的片段(一个更好地将候选结果集的价值传达给招聘者的片段)的情况下,实验组的预约率应该高于对照组。

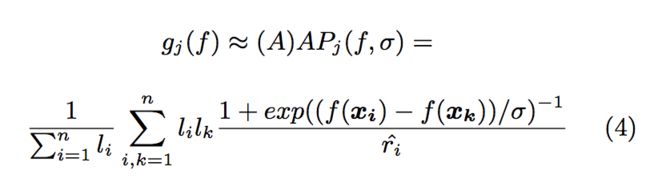
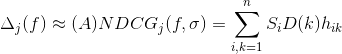
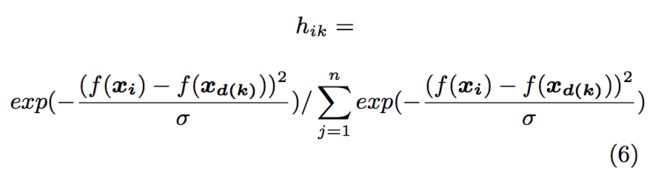
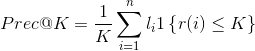
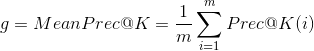
![\Delta =\Delta _{SSE}(H_s, H_e) = \sum_{i=1}^{b}(H_s[i] - H_e[j])^2](http://img.e-com-net.com/image/info8/741c3e76e2f84885b8209335e921bc29.gif)