曼哈顿距离最小生成树

一、前人种树

博客：曼哈顿距离最小生成树与莫队算法

博客：学习总结：最小曼哈顿距离生成树

 

二、知识梳理

曼哈顿距离：给定二维平面上的N个点，在两点之间连边的代价。（即distance(P1,P2) = |x1－x2|+|y1－y2|）

曼哈顿距离最小生成树问题求什么？求使所有点连通的最小代价。

最小生成树的“环切”性质：在图G = (V, E)中，如果存在一个环，那么把环上的最大边e删除后得到的图G’ = (V, E- {e})的最小生成树的边权和与G相同。

 

三、难点剖析

【废话定理神马的，很难懂只要记住就是了】

朴素的算法可以用O(N²)的Prim，或者处理出所有边做Kruskal，但在这里总边数有O(N²)条，所以Kruskal的复杂度变成了O(N²logN)。  

但是事实上，真正有用的边远没有O(N²)条。我们考虑每个点会和其他一些什么样的点连边。

可以得出这样一个结论：以一个点为原点建立直角坐标系，在每45度内只会向距离该点最近的一个点连边。

证明结论：假设我们以点A为原点建系，考虑在y轴向右45度区域内的任意两点B(x1,y1)和C(x2,y2)，不妨设|AB|≤|AC|（这里的距离为曼哈顿距离），如下图：

|AB|=x1+y1，|AC|=x2+y2，|BC|=|x1-x2|+|y1-y2|。而由于B和C都在y轴向右45度的区域内，有y-x>0且x>0。下面我们分情况讨论：

1. x1>x2且y1>y2。这与|AB|≤|AC|矛盾；
2. x1≤x2且y1>y2。此时|BC|=x2-x1+y1-y2，|AC|-|BC|=x2+y2-x2+x1-y1+y2=x1-y1+2*y2。由前面各种关系可得y1>y2>x2>x1。假设|AC|<|BC|即y1>2*y2+x1，那么|AB|=x1+y1>2*x1+2*y2，|AC|=x2+y2<2*y2<|AB|与前提矛盾，故|AC|≥|BC|；
3. x1>x2且y1≤y2。与2同理；
4. x1≤x2且y1≤y2。此时显然有|AB|+|BC|=|AC|，即有|AC|>|BC|。

综上有|AC|≥|BC|，也即在这个区域内只需选择距离A最近的点向A连边。

这种连边方式可以保证边数是O(N)的，那么如果能高效处理出这些边，就可以用Kruskal在O(NlogN)的时间内解决问题。下面我们就考虑怎样高效处理边。

我们只需考虑在一块区域内的点，其他区域内的点可以通过坐标变换“移动”到这个区域内。为了方便处理，我们考虑在y轴向右45度的区域。在某个点A(x0,y0)的这个区域内的点B(x1,y1)满足x1≥x0且y1-x1>y0-x0。这里对于边界我们只取一边，但是操作中两边都取也无所谓。那么|AB|=y1-y0+x1-x0=(x1+y1)-(x0+y0)。在A的区域内距离A最近的点也即满足条件的点中x+y最小的点。因此我们可以将所有点按x坐标排序，再按y-x离散，用线段树或者树状数组维护大于当前点的y-x的最小的x+y对应的点。时间复杂度O(NlogN)。

至于坐标变换，一个比较好处理的方法是第一次直接做；第二次沿直线y=x翻转，即交换x和y坐标；第三次沿直线x=0翻转，即将x坐标取相反数；第四次再沿直线y=x翻转。注意只需要做4次，因为边是双向的。

至此，整个问题就可以在O(NlogN)的复杂度内解决了。

【回到正题】

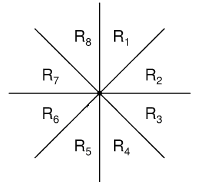
一个点把平面分成了8个部分：

由上面的废话可知，我们只需要让这个点与每个部分里距它最近的点连边。

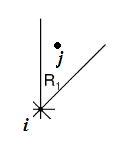
拿R1来说吧：

如图，i的R1区域里距i最近的点是j。也就是说，其他点k都有：

x_j + y_j <= x_k + y_k

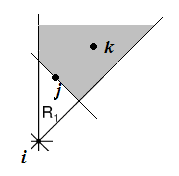
那么k将落在如下阴影部分：

显然，边(i,j), (j,k), (i,k)构成一个环，而(i,k)一定是最长边，可以被删去。所以我们只连边(i,j)。

为了避免重复加边，我们只考虑R1~R4这4个区域。（总共加了4N条边）

这4个区域的点(x,y)要满足什么条件？

• 如果点(x,y)在R1，它要满足：x ≥ xi ,y – x ≥ yi – xi（最近点的x + y最小）
• 如果点(x,y)在R2，它要满足：y ≥ yi ,y – x ≤ yi – xi（最近点的x + y最小）
• 如果点(x,y)在R3，它要满足：y ≤ yi ,y + x ≥ yi + xi（最近点的y – x最小）
• 如果点(x,y)在R4，它要满足：x  ≥ xi ,y + x ≤ yi – xi（最近点的y – x最小）

其中一个条件用排序，另一个条件用数据结构（这种方法很常用），在数据结构上询问，找最近点。因为询问总是前缀或后缀，所以可以用树状数组。

 

四、代码模板

//离散化：
	scanf("%d", &N);
	for (int i=1; i<=N; ++i)
	{
		scanf("%d%d", &P[i].x, &P[i].y);
		P[i].id = i;
		P[i].d = P[i].y - P[i].x;
		P[i].s = P[i].y + P[i].x;
	}
	//对x,y离散化
	int totxy = 0;
	for (int i=1; i<=N; ++i)
	{
		xy[totxy++] = P[i].x;
		xy[totxy++] = P[i].y;
	}
	sort(xy, xy+totxy);
	for (int i=1; i<=N; ++i)
	{
		P[i].idx = lower_bound(xy, xy+totxy, P[i].x) - xy + 1;
		P[i].idy = lower_bound(xy, xy+totxy, P[i].y) - xy + 1;
	}

//树状数组：
struct BIT
{
	pii a[maxN * 2];
	int N;
	void Init(int _N)
	{
		N = _N;
		for (int i=0; i<=N; ++i) a[i] = pii(oo, 0);
	}
	pii ask(int x)
	{
		return x == 0 ? pii(oo, 0) : min(a[x], ask(x - (x & (-x))));
	}
	void update(int x, const pii &v)
	{
		if (x > N) return ;
		a[x] = min(a[x], v);
		update(x + (x & (-x)), v);
	}
	
	pii ask_front(int x) {return ask(x);}
	pii ask_back(int x) {return ask(N - x + 1);}
	void update_front(int x, const pii &v) {update(x, v);}
	void update_back(int x, const pii &v) {update(N - x + 1, v);}
} tree;

//构图：
bool cmp1(const Tpoint &A, const Tpoint &B) 
{
	//return A.x < B.x || (A.x == B.x && A.y < B.y);
	return (A.y - A.x > B.y - B.x || A.y - A.x == B.y - B.x && A.x > B.x);
}
bool cmp2(const Tpoint &A, const Tpoint &B) 
{
	//return A.x < B.x || (A.x == B.x && A.y > B.y);
	return (A.y + A.x < B.y + B.x || A.y + A.x == B.y + B.x && A.x > B.x);
}
bool cmp3(const Tpoint &A, const Tpoint &B) 
{
	//return A.y < B.y || (A.y == B.y && A.x < B.x);
	return A.y - A.x < B.y - B.x || A.y - A.x == B.y - B.x && A.y > B.y;
}
bool cmp4(const Tpoint &A, const Tpoint &B) 
{
	//return A.y < B.y || (A.y == B.y && A.x > B.x);
	return A.s > B.s || A.s == B.s && A.y < B.y;;
}

bool cmpE(const E_arr &A, const E_arr &B) {return A.v < B.v;} 

void Make_Graph()
{
	#define Connect(i,j) E[++tot_E].Init(P[i].id,P[j].id,getdis(i,j))
	
	int LL, RR;
	
	tree.Init(2 * N);
	sort(P+1, P+N+1, cmp1);
	for (int i=1; i<=N; ++i)
	{
		pii tmp = tree.ask_back(P[i].idx);
		if (tmp.first < oo) Connect(i, tmp.second);
		tree.update_back(P[i].idx, pii(P[i].x + P[i].y, i));
	}
	
	sort(P+1, P+N+1, cmp2);
	tree.Init(2 * N);
	for (int i=1; i<=N; ++i)
	{
		pii tmp = tree.ask_back(P[i].idx);
		if (tmp.first < oo) Connect(i, tmp.second);
		tree.update_back(P[i].idx, pii(P[i].x - P[i].y, i));
	}
	
	sort(P+1, P+N+1, cmp3);
	tree.Init(2 * N);
	for (int i=1; i<=N; ++i)
	{
		pii tmp = tree.ask_back(P[i].idy);
		if (tmp.first < oo) Connect(i, tmp.second);
		tree.update_back(P[i].idy, pii(P[i].x + P[i].y, i));
	}
	
	sort(P+1, P+N+1, cmp4);
	tree.Init(2 * N);
	for (int i=1; i<=N; ++i)
	{
		pii tmp = tree.ask_front(P[i].idy);
		if (tmp.first < oo) Connect(i, tmp.second);
		tree.update_front(P[i].idy, pii(P[i].x - P[i].y, i));
	}
}

 

五、沙场练兵

POJ 3241 Object Clustering 求曼哈顿距离最小生成树上第k大的边

//POJ3241; Object Clustering; Manhattan Distance MST
#include 
#include 
#include 
#define N 100000
#define INFI 123456789

struct point
{
	int x, y, n;
	bool operator < (const point &p) const
	{ return x == p.x ? y < p.y : x < p.x; }
}p[N + 1];
struct inedge
{
	int a, b, w;
	bool operator < (const inedge &x) const
	{ return w < x.w; }
}e[N << 3 | 1];
struct BITnode
{
	int w, p;
}arr[N + 1];
int n, k, tot = 0, f[N + 1], a[N + 1], *l[N + 1], ans;

template 
inline T abs(T x)
{ return x < (T)0 ? -x : x; }

int find(int x)
{ return x == f[x] ? x : f[x] = find(f[x]); }

inline bool cmp(int *a, int *b)
{ return *a < *b; }

inline int query(int x)
{
	int r = INFI, p = -1;
	for (; x <= n; x += x & -x)
		if (arr[x].w < r) r = arr[x].w, p = arr[x].p;
	return p;
}

inline void modify(int x, int w, int p)
{
	for (; x > 0; x -= x & -x)
		if (arr[x].w > w) arr[x].w = w, arr[x].p = p;
}

inline void addedge(int a, int b, int w)
{
	++tot;
	e[tot].a = a, e[tot].b = b, e[tot].w = w;
//	printf("%d %d %d\n", a, b, w);
}

inline int dist(point &a, point &b)
{ return abs(a.x - b.x) + abs(a.y - b.y); }

int main()
{
	//Initialize
	scanf("%d%d", &n, &k);
	for (int i = 1; i <= n; ++i)
	{
		scanf("%d%d", &p[i].x, &p[i].y);
		p[i].n = i;
	}
	//Solve
	for (int dir = 1; dir <= 4; ++dir)
	{
		//Coordinate transform - reflect by y=x and reflect by x=0
		if (dir == 2 || dir == 4)
			for (int i = 1; i <= n; ++i) p[i].x ^= p[i].y ^= p[i].x ^= p[i].y;
		else if (dir == 3)
			for (int i = 1; i <= n; ++i) p[i].x = -p[i].x;
		//Sort points according to x-coordinate
		std::sort(p + 1, p + n + 1);
		//Discretize
		for (int i = 1; i <= n; ++i) a[i] = p[i].y - p[i].x, l[i] = &a[i];
		std::sort(l + 1, l + n + 1, cmp);
		/*
		int cnt = 1;
		for (int i = 2; i <= n; ++i)
			if (*l[i] != *l[i - 1]) *l[i - 1] = cnt++;
			else *l[i - 1] = cnt;
		*l[n] = cnt;
		*/
		for (int i = 1; i <= n; ++i) *l[i] = i;
		//Initialize BIT
		for (int i = 1; i <= n; ++i) arr[i].w = INFI, arr[i].p = -1;
		//Find points and add edges
		for (int i = n; i > 0; --i)
		{
			int pos = query(a[i]);
			if (pos != -1)
				addedge(p[i].n, p[pos].n, dist(p[i], p[pos]));
			modify(a[i], p[i].x + p[i].y, i);
		}
	}
	//Kruskal
	std::sort(e + 1, e + tot + 1);
	for (int i = 1; i <= n; ++i) f[i] = i;
	for (int i = 1, ec = n; ec > k && i <= tot; ++i)
		if (find(e[i].a) != find(e[i].b))
		{
			f[find(e[i].a)] = find(e[i].b);
			if (--ec == k) ans = e[i].w;
		}
	printf("%d\n", ans);
	return 0;
}

转载于:https://www.cnblogs.com/xzxl/p/7237246.html