简单の暑假总结——最小生成树

6.1 最小生成树

我们先来了解一下最小生成树的概念：

我们定义无向连通图的 最小生成树（Minimum Spanning Tree，MST）为边权和最小的生成树（树也叫做生成树）。——OI Wiki

我们举一个例子：

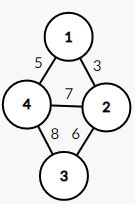
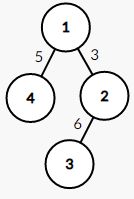
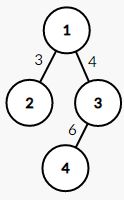
在这样一个带权无向图中，它的最小生成树如下图所示，其权值为 $14$

我们有 $2$ 种算法来解决这个问题

6.2 Prim 算法

Prim 算法无论是本质上还是代码上都与 Dijkstra 高度类似，本质上还是一个贪心，它将图中所有的结点分为了两种，一种是已经塞入了最小生成树的结点，一种是还没有塞入了最小生成树 的结点。

每一次操作时，我们在还没有塞入了最小生成树 的结点中找到一个与已经塞入了最小生成树的结点中路径最短的（即 $dis[i]$ 最小），将该结点标记为已经塞入了最小生成树的结点，并更新该结点周围结点的的 $dis[i]$

一般情况下，我们以 $1$ 号结点作为起点开始遍历

6.2.1 演示时间

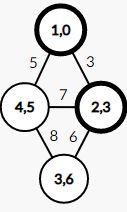
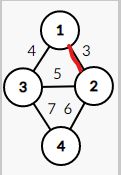
拿下图举例：

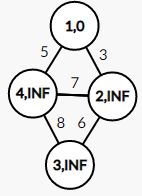
对于每一个结点，逗号前的数值表示序号，逗号后的元素表示该结点对应的 $dis[i]$ 的值

因为以 $1$ 号结点作为起点，所以 $dis[i]=0$

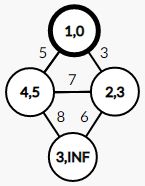
第一次遍历后，我们就将 $1$ 号结点作上了标记（表明压入了最小生成树），并更新 $dis[2]$ 和 $dis[4]$

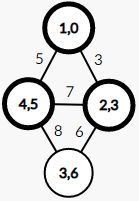
第二次操作，在未被标记的点中找的一个 $dis$ 值最小的，进行相应的处理

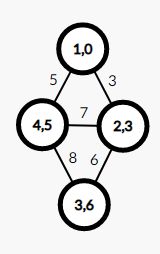
依葫芦画瓢的，我们得到了第三步操作后的结果：

自然，最后一步结果显然得出：

所以这跟 Dijkstra 有什么差别呢？

只需要注意，在每一次更新之前，我们都需要将 $dis[i]$ 累加给答案

当然， Prim 算法也有优化

6.2.2 Prim 算法的优化

真的， Prim 算法的优化甚至跟 Dijkstra 算法的优化一模一样！

如果你不会优化 Dijkstra ，Go to here

话说不会的不是可以回炉重造了吗?

6.2.3 裸题讲解（话说裸题还要讲解？）

Eg_1 最小生成树

这应该不需要讲解吧

代码如下：

#include
#include
using namespace std;
priority_queue<pair<int,int> > q;
const int N=1000005;
int head[N],Next[N],ver[N],edge[N],len;
int dis[N],vis[N];
int n,m,x,y,z;
long long int MST;			//10年OI一场空，不开 long long 见祖宗
void add(int x,int y,int z){
	ver[++len]=y,edge[len]=z,Next[len]=head[x],head[x]=len;
}			//链式前向星模板
void Prim(){
	for(int i=1;i<=n;i++){
		dis[i]=0x3f3f3f3f;
	}
	dis[1]=0;
	q.push(make_pair(0,1));
	while(!q.empty()){
		int xx=q.top().second;
		q.pop();
		if(vis[xx]){
			continue;
		}			//堆优化
		vis[xx]=1;
		MST+=dis[xx];			//将权值累加给答案
		for(int i=head[xx];i;i=Next[i]){
			int yy=ver[i],zz=edge[i];
			if(dis[yy]>zz){
				dis[yy]=zz;
				q.push(make_pair(-dis[yy],yy));
			}			//链式前向星优化
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z),add(y,x,z);
	}
	Prim();
	printf("%lld",MST);
	return 0;
}
//基本上和 Dijkstra 一模一样

6.3 Kruskal 算法

Kruskal 本质上还是一种贪心，但在代码方面，是通过并查集实现的

我们需要将所有的边按照顺序从小到大依次排列，然后，对于每一条边，判断其端点是否在同一集合内，如果是，说明加入这条边后，会出现环，不能要；反之，我们就将这两个端点塞进同一个集合里，并累加答案

6.3.1 演示时间

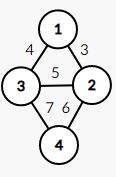
举个例子：

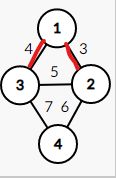
我们按照排序后选择的第一条边为权值为 $3$ 的边

此时，我们将答案累加 $3$ ，并将 $1$ 号结点和 $2$ 号结点塞入同一集合内

下一步，我们应该处理边权为 $4$ 的边

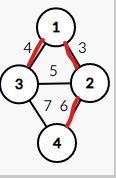
下一步，我们应该处理边权为 $5$ 的一条边，但是，因为 $2$ 号结点和 $3$ 号结点已经在同一集合内了，所以不处理边权为 $5$ 的这条边，转去处理边权为 $6$ 的边

此时，我们也就得到了最小生成树，其边权和为 $13$

6.3.2 例题讲解

Eg_2 最小生成树

怎么又是你？

裸题，kruskal 版代码如下

#include
#include
using namespace std;
struct node{
	int x,y,z;			//存贮每一条边
}a[1000005];
int n,m,x,y,z,sum,fa[1000005];
long long int MST;
int find(int num){
	if(fa[num]==num){
		return num;
	}
	return fa[num]=find(fa[num]);
}			//在 kruskal 算法中，我们只需要 find 函数即可
bool cmp(node a,node b){
	return a.z<b.z;
}
void Kruskal(){
	sort(a+1,a+1+m,cmp);			//按权值顺序进行排序
	for(int i=1;i<=m;i++){
		int xx=find(a[i].x),yy=find(a[i].y);			//取出每一条边的两个端点
		if(xx==yy){			//如果在同一集合内
			continue;
		}
		MST+=a[i].z;
		fa[xx]=yy;
		sum++;
		if(sum==n){
			return ;
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		fa[i]=i;
	}			//并查集初始化
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
	}			//输入边
	Kruskal();
	printf("%lld",MST);
	return 0;
}

6.4 输出最小生成树的边

个人认为用 Kruskal 算法求边是很简单的

考虑下面的代码

int xx=find(a[i].x),yy=find(a[i].y);		
if(xx==yy){			
	continue;
}
MST+=a[i].z;

如果我们没有执行 if 语句，说明我们选择了当前这条边，并且，相对于 Prim 算法，我们是很容易求两边的两个端点的

所以，我们只需要在 if 语句后面，将两个端点塞入一个答案数组中，最后输出即可

Eg_3 城市公交网建设问题

谢天谢地，终于不是裸题了

根据上面的思路，我们还是很容易打出代码的

#include
#include
using namespace std;
const int N=200005;
struct node{
	int x,y,z;
}a[N],ans[N];
int fa[N],n,m,x,y,z,cnt,sum;
int find(int num){
	if(fa[num]==num){
		return num;
	}
	return fa[num]=find(fa[num]);
}
bool cmp(node a,node b){
	return a.z<b.z;
}
void Kruskal(){			//个人喜好，一般用 Kruskal 求路径
	sort(a+1,a+1+m,cmp);
	for(int i=1;i<=m;i++){
		int xx=find(a[i].x),yy=find(a[i].y);
		if(xx==yy){
			continue;
		}
		fa[xx]=yy;			//以上所有都为 Kruskal 模板
		ans[++cnt].x=a[i].x,ans[cnt].y=a[i].y;			//将该点的两个端点塞入答案数组
		sum++;
		if(sum==n){
			return ;
		}
	}
}
bool cmp1(node a,node b){
	if(a.x!=b.x){			//以左端点为第一关键字，右端点为第二关键字进行排序
		return a.x<b.x;
	}
	return a.y<b.y;
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		fa[i]=i;
	}
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
		if(a[i].x>a[i].y){
			swap(a[i].x,a[i].y);			//方便后面的排序，反正也是无向图
		}
	}
	Kruskal();
	sort(ans+1,ans+1+cnt,cmp1);			//排序
	for(int i=1;i<=cnt;i++){
		printf("%d %d\n",ans[i].x,ans[i].y);			//输出
	}
	return 0;
}