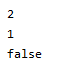读书笔记-算法与数据结构(第二版java)
进行了一次笔试,深切的感受到了自己在数据结构方面的知识的零散,因此专门找一本书来系统的整理学习一下,最后发现Java数据结构和算法这本书系统性比较强,而且内容浅显易懂,因此通过这本书作为载体来进行学习,顺便记录一下重点。
一:综述
1.为什么要用数据结构?
我们使用的数据结构和数据跟我们现实世界数据存储紧密相连,例如索引卡片,我们在上面记录了姓名,电话,住址。
虽然我们可以很简单的将索引卡片转化为计算机中存储的数据,但是在计算机世界中会遇到以下几个问题:
如何在计算机中安放数据?
这种方法适合安放10张,但是1000张100000张呢?
如何保证快速的插入新卡片?删除旧卡片?
需不需要排序?怎样排序?
怎样跨苏查找一个我们需要的卡片?
由此产生了我们对于数据结构与算法的协同配合产生了基本的程序,这就是程序=数据结构+算法的基本含义。
2.数据结构的概述
| 数据结构 | 优点 | 缺点 |
|---|---|---|
| 数组 | 插入快,知道下表,可以快速存取 | 删除慢,查找慢,大小固定 |
| 有序数组 | 比无序数组查找块 | 删除慢,大小固定 |
| 栈 | 提供后进先出的存取 | 存取其它项很慢 |
| 队列 | 提供先进先出的存取 | 存取其它项很慢 |
| 链表 | 插入快,删除快 | 查找慢 |
| 二叉树 | 查找、插入、删除都很快(如何保持二叉树的平衡) | 删除算法复杂 |
| 红-黑树 | 查找、插入、删除都很快(树总是平衡的) | 算法很复杂 |
| 2-3-4树 | 查找、插入、删除都很快(树总是平衡的)类似的树对磁盘存储有用 | 算法复杂 |
| 哈希表 | 如果关键字已知,则存取极快 | 删除慢,如果关键字未知则存取慢,对空间利用不充分 |
| 堆 | 插入、删除快,对最大快数据块的存取很快 | 对其他数据项存取复杂 |
| 图 | 对现实世界的建模 | 有些算法很复杂 |
3.算法的概述
许多算法直接用于某些数据结构,对于每种数据结构都需要知道:
如何插入一条新数据;
如何查找一条特定的数据;
如何删除一条数据;
迭代的访问数据结构的每一条数据;
如何排序;
递归的调用自身。
二:数组
1.查找
(1)顺序查找:很简单,不再赘述,时间复杂度为O(n),空间复杂度O(1)
(2)二分查找:一直不太清楚二分查找的时间复杂度log2(n)是怎么算出来的,接下来进行具体分析。
例如:对于猜数游戏

由上图可知:对于猜数范围越大,利用二分查找查找的次数越小,其中 2的10次方为1024,2的7次方为128,类推下去可以知道二分查找n个数据的时间复杂度最大为log2(n)。
对于大“O”表示法,为了加快我们的计算效率,对于A算法比B算法快两倍是没有什么意义的 。
由于log2(N) = 2.333*log(N),当我们利用大“O”表示法时可以直接表示为O(log(N))。
同时汇总线性与二分查找、插入、删除的表格

三.简单排序
包括冒泡排序,选择排序和插入排序,冒泡排序过于简单,对于数据量很小的排序比较适用,但是对于数据量较大的几乎不考虑。
1.简单选择排序
例如:
排成一排的NBA运动员此时是无序排列的,我们对于将所有的运动员一次扫一遍,选出最矮的运动员与队尾的运动员进行交换,然后选择出第二矮的运动员进行交换。
public class SelectSort {
public static void main(String[] args) {
int[] arr = new int[]{1,3,2,5,2,7,3};
for(int i = 0; i < arr.length-1;i++){
int k = i;
int j = i + 1;
for(; j < arr.length; j++){
if(arr[k] > arr[j]){k = j;}
}
if(k != j){
int temp = arr[i];
arr[i] = arr[k];
arr[k] = temp;
}
}
for(int i:arr)
System.out.print(i+" ");
}
}
![]()
2.插入排序
插入排序实际上是对于一部分已经排好序的数组进行插入,找到合适的插入位置之后,对于其后数据依次后移。
public class InsertSort {
public static void main(String[] args) {
int[] arr = new int[]{1,5,2,5,8,2,0,3};
for(int i = 1; i < arr.length; i++){
if(arr[i] < arr[i-1]){
int temp = arr[i];
arr[i] = arr[i-1];
int j = i-1;
for(;j >= 0 && arr[j] > temp; j--){
arr[j+1] = arr[j];
}
arr[j + 1] = temp;
}
}
for(int i:arr){
System.out.print(i+" ");
}
}
}
选择排序虽然把数据量降到了最低,但是次数依然很大。对于基本有序的数组可以选择插入排序,但是对于数据量较大的数组选择插入排序依然不是好的方法,可以考虑快速插入排序。
四:栈和队列
栈和队列一般作为程序员的辅助工具,而不是存储形式,一般会在需要时创建,在不需要时销毁,它的生命周期比数组短的多。
1.栈
先进后出(FILO)访问形式:即只能访问最后一个入栈的数据。
栈在解析运算表达式的时候占据了重要作用,比如解析3*(4+5)。
在Java中简单的方法:
public static void main(String[] args) {
Stack<Integer> sta = new Stack<>();
sta.push(1); //存数据
sta.push(2);
System.out.println(sta.pop());//取数据
System.out.println(sta.peek());//读取头数据但不取出来
System.out.println(sta.empty());//判断是否为空栈
}
public static String doRev(String input){
Stack<Character> sta = new Stack<>();
for(int i = 0; i < input.length(); i++){
sta.push(input.charAt(i));
}
String output = "";
while(!sta.empty()){
output += sta.pop();
}
return output;
}
例子2:分隔符匹配
分割符包括“{”和“}”,“(”和“)”,“[”和“]”。
思路:遇到做分割符则压入栈中,遇到右分隔符则取出头数据,判断是否为对应的右分隔符,若不符合,则输出"Erro"并且输出分隔符索引位置;成功则输出“Success”。
public static void check(String input){
Stack<Character>sta = new Stack<>();
for(int j = 0; j < input.length();j++){
char ch;
switch (ch = input.charAt(j)){
case '{':
case '[':
case '(':sta.push(ch);break;
case '}':
case ']':
case ')':
if(!sta.empty()){
char chx = sta.pop();
if((chx == '}' && ch == '{') || (chx == ']' && ch == '[') || (chx == ')' && ch == '(')) break;
else System.out.println("Erro"+ ch + "at" + j);
}else{
System.out.println("Erro"+ ch + "at" + j);
}
break;
default:break;
}
}
if(sta.empty())
System.out.println("Success");
else System.out.println("Erro" + sta.pop() + "at" + 0);
}
栈是一种可以对其他应用了相当难度算法的数据结构的便利工具,如对于二叉树的遍历,利用栈查找图的顶点(迷宫问题)。
2.队列
队列可以说是“排”,是一种先进先出的存储结构(FIFO)。
主要方法:
| 操作 | 方法 | 方法2 | 备注 |
|---|---|---|---|
| 插入 | add(e) | offer(e) | 插入一个元素 |
| 移除 | remove() | poll() | 移除和返回队列的头 |
| 检查 | element() | peek() | 返回但不移除队列的头 |
Queue<Integer> queue = new ArrayQueue<>();
queue.add(1);//队尾添加数据
queue.add(2);
System.out.println(queue.peek());//读取队头数据
System.out.println(queue.poll());//拿出对头数据
System.out.println(queue.peek());
输出为:
![]()
3.优先级队列
优先级队列是比栈和队列跟有用的数据结构,跟普通队列一样,优先级队列也有队头队尾,并且也是从队头移除数据。不过在优先级队列中,数据项值按照关键字有序排列,这样关键字数据最小的元素总是在队头。数据插入的时候也会按照关键字有序插入优先级队列中以确保队列的顺序。
应用:图的最小生成树的算法;
抢占式多任务操作系统;
寻找最便宜的方法或者最短路径;
除了实现快速关键字的查找外,优先级队列可以进行快速的插入,因此,优先级队列通常采用堆的方式实现。
Queue<String> priqueue = new PriorityQueue<>();
priqueue.add("b");
priqueue.add("a");
priqueue.add("c");
System.out.println(priqueue.poll());
System.out.println(priqueue.poll());
System.out.println(priqueue.peek());
输出:
可以看出输入顺序为bac,但是输出顺序为abc,可以看出已经进行自动排序。
应用:解析算数表达式
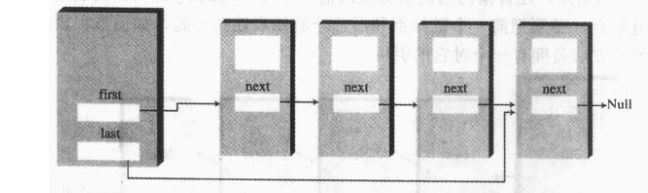
五.链表
链表有一种非常灵活的机制,能够解决数组在有序时插入效率低,无序时查找效率低的问题,它可以取代数组,可以普遍应用于栈和队列的有一种基础数据结构。
链表有单链表,双向链表,有序链表,双向链表和有迭代器的链表(迭代器是一种随机访问链表元素的一种方法)。
链表的效率
增加元素的时候,如果在链表头或链表尾,只需要增加一次就可以。
平均起来,增减,删除和替换都需要N/2次,跟数组相同,但是相对于数组仍然有优势,如果增删有比较大的数据量时,使用链表复制更加节约时间。
而且,链表的元素数目是可以增减的,可以增加到任意可以可扩展到的存储范围,但是数组的范围是不可改变的,超过边界就不可执行了。
1.单链表
2.双端链表
六.递归
递归需要注意两点:
一是找到调用自身的函数与参数;二是找到截止条件。
效率分析:
在使用递归时只是在概念上简化了它,并不是说明它有效率,相反,调用一个方法都会有额外的开销,并且传递方法都需要把这个方法地址和方法参数压入栈中,让我们知道访问的方法和需要用到的参数。
另一个低效性体现在中间存储的大量参数和返回值都需要存储在栈中,如果数据量过多可能会导致栈溢出。
递归的二分查找
查找条件:数据是有序的。
方法:首先将数据分成两半,选取中间数据跟要查找的值进行比较,如果中间数据等于查找值,那么直接结束循环,如果查找值大于中间数据,那么可以确定查找值在后半段,然后则进行后半段的查找;反之,在前半段查找。
代码如下所示,
public class Bsearch {
public static void main(String[] args) {
int[] nums = new int[]{1,2,3,4,5,6,7,8,9,10};
besarchFind(nums,0,nums.length-1,3);
}
public static void besarchFind(int[] nums,int start,int end,int key){
int mid = (start + key) / 2;
if(nums[mid] == key) System.out.println("位置索引:"+mid);
else if(nums[mid] < key){
start = mid + 1;
besarchFind(nums,start,end,key);
}else {
end = mid - 1;
besarchFind(nums,start,end,key);
}
}
}
递归的归并排序
六.二叉树
七.堆
八.图
1.搜索
深度优先搜索
遍历步骤:
(1).设置搜索指针p,使p指向顶点v;
(2).访问p所指顶点,并使p指向与其相临接的尚未被访问过的顶点;
(3).若p所指向的顶点存在,则重复步骤(2);
(4).沿着刚才访问的次序和方向回溯到一个尚有临接顶点且尚未被访问过的顶点,并使p指向这个尚未访问的顶点,然后重复步骤(2),直道所有顶点都被访问。
遍历的关键在于判断结点是否被访问过,这就需要利用邻接矩阵来判断。怎么做呢?首先找到顶点所在的行,然后从左到右判断与所在顶点为1,也就是跟所在顶点相连的点,如果有1,则进一步到这个列顶点,作为行顶点,继续访问,如果没有,说明这个顶点已经遍历完毕了。
代码实现方法:
public static int getUnvisistVertex(int v){
for(int i = 0; i < graphic[v].length-1; i++){
if(graphic[v][i]) return i;
}
return -1;
}
这样就可以访问得出一个顶点是否有临接但还没有访问的顶点了。
接下来就需要进行DFS的操作了,具体操作要借用栈工具,在执行循环的时候直到栈为空才会才会认为遍历完成了,具体需要如下四部操作:
(1)用peek()检查栈顶点;
(2)试图找到这个栈顶未访问的临接点;
(3)如果没有占到,则直接出栈,如果找到,入栈作为栈顶元素;
(4)直到栈顶为空
public static void dfs(boolean[][] garphic,int v){
System.out.println("第一个结点"+v);
sta.push(v);
while(!sta.empty()){
int x = getUnvisistVertex(sta.peek());
if(x == -1){
int n = sta.pop();
System.out.println(n+"的结点连接是空的了");
}else{
System.out.println(v+"的下一个非空结点是"+x);
v = sta.peek();
graphic[v][x] = false;
graphic[x][v] = false;
sta.push(x);
System.out.println("访问了"+x);
}
}
}
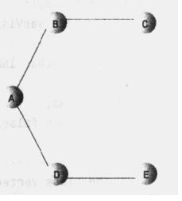
如图所示进行遍历:
我们将上图ABCDE变为0,1,2,3,4进行遍历,上图可以建立图表,如果两个顶点相连则为true,如果不相连就为false,建立临接矩阵为:
static boolean[][] graphic = {{false,true,false,true,false},{true,false,true,false,false},
{false,true,false,false,false}, {true,false,false,false,true},{false,false,false,true,false}};
public static void main(String[] args) {
for(int i = 0; i < graphic.length; i++){
for(int j = 0; j < graphic[i].length; j++){
System.out.print(graphic[i][j]+" ");
}
System.out.print("\n");
}
dfs(graphic,0);
for(int i = 0; i < graphic.length; i++){
for(int j = 0; j < graphic[i].length; j++){
System.out.print(graphic[i][j]+" ");
}
System.out.print("\n");
}
}
总程序:
import java.util.Stack;
public class getVertex {
static boolean[][] graphic = {{false,true,false,true,false},{true,false,true,false,false},
{false,true,false,false,false}, {true,false,false,false,true},{false,false,false,true,false}};
static Stack<Integer> sta = new Stack<>();
public static void main(String[] args) {
for(int i = 0; i < graphic.length; i++){
for(int j = 0; j < graphic[i].length; j++){
System.out.print(graphic[i][j]+" ");
}
System.out.print("\n");
}
dfs(graphic,0);
for(int i = 0; i < graphic.length; i++){
for(int j = 0; j < graphic[i].length; j++){
System.out.print(graphic[i][j]+" ");
}
System.out.print("\n");
}
}
public static void dfs(boolean[][] garphic,int v){
System.out.println("第一个结点"+v);
sta.push(v);
while(!sta.empty()){
int x = getUnvisistVertex(sta.peek());
if(x == -1){
int n = sta.pop();
System.out.println(n+"的结点连接是空的了");
}else{
System.out.println(v+"的下一个非空结点是"+x);
v = sta.peek();
graphic[v][x] = false;
graphic[x][v] = false;
sta.push(x);
System.out.println("访问了"+x);
}
}
}
public static int getUnvisistVertex(int v){
for(int i = 0; i < graphic[v].length; i++){
if(graphic[v][i] == true) return i;
}
return -1;
}
}

*广度优先搜索
图的广度优先搜索方法为:图的某个顶点v出发,在访问了v之后依次访问各个未被访问的临接点,并使“先被访问的临接点”先于“后被访问的临接点”被访问,直到图中临接点都被访问到。
广度优先搜索遍历的特点是尽可能的先进行横向搜索,即最先访问的顶点的临接点也最先被访问,为此,引入队列来保存已访问过的顶点,当队头出队时就访问这个顶点的临接点,并将这些临接点依次入队。
代码如下,思路:跟深度优先搜索类似,不同的是,广度搜索使用队列来存储节点元素,每次出队列元素,对这个队列进行搜索,如果有临接点未被访问,则入队列,直到访问完成队列的所有元素。
import java.util.ArrayDeque;
import java.util.Queue;
public class BFSearch {
static boolean[][] graphic = {{false,true,false,true,false},{true,false,true,false,false},
{false,true,false,false,false}, {true,false,false,false,true},{false,false,false,true,false}};
static Queue<Integer> queue = new ArrayDeque<>();
public static void main(String[] args) {
for(int i = 0; i < graphic.length; i++){
for(int j = 0; j < graphic[i].length; j++){
System.out.print(graphic[i][j]+" ");
}
System.out.print("\n");
}
BFS(graphic,0);
for(int i = 0; i < graphic.length; i++){
for(int j = 0; j < graphic[i].length; j++){
System.out.print(graphic[i][j]+" ");
}
System.out.print("\n");
}
}
public static void BFS(boolean[][] graphic,int v){
queue.offer(v);
System.out.println("访问"+v);
while(!queue.isEmpty()){
int n = getVerPoint(v);
while(n != -1){
queue.offer(n);
System.out.println("访问"+n);
graphic[v][n] = false;
graphic[n][v] = false;
n = getVerPoint(v);
}
v = queue.remove();
}
}
public static int getVerPoint(int v){
for(int i = 0 ; i < graphic[v].length; i++){
if(graphic[v][i] == true) return i;
}
return -1;
}
}
有权无向图的最小生成树

对于有权无向图的最小生成树的求法主要有两种:
一是普里姆(Prim)算法,二是克鲁斯卡尔(Kruskal)算法。
首先简要对这种两种方法进行介绍,然后对Kruskal算法进行编程。
Prim算法:如图所示,简而言之就是不断从已生成树选择这些可以和树连接的但是还没有连接的顶点最小的连接还没有被连接的顶点
import java.util.ArrayList;
import java.util.List;
public class KruskalDemo {
static int[][] graphic = new int[][]{{Integer.MAX_VALUE,6,9,5,13},
{6,Integer.MAX_VALUE,6,7,8 },
{9,6,Integer.MAX_VALUE,9,3 },
{5,7,9,Integer.MAX_VALUE,3 },
{13,8,3,3,Integer.MAX_VALUE}};
public static void main(String[] args) {
List<Integer> list = new ArrayList<>();
list.add(0);
int point = 0 ;
while(list.size() < graphic.length){
int weight = Integer.MAX_VALUE;
for(int m:list){
int n = 0;
for(int i = 0; i < graphic.length; i++){
if(!list.contains(i)) {
n = i;
break;
}
}
for(; n < graphic.length ; n++){
if( !list.contains(n)&& graphic[m][n] <= weight){
point = n;
weight = graphic[m][n];
}
}
}
list.add(point);
}
for(int i :list) System.out.print(i+"->");
}
}
Prim程序代码:
算法要点:找到一个一个顶点,并且把它放入树的集合中,
(1)找到这个顶点连接到新的并且不在集合中的顶点的边,并且放入优先队列;
(2)找到这个权值的最小边,并且把这条边的顶点放入集合中。
重复这些步骤,直到所有的顶点都在集合中。
Kruskal算法:算法图解如下所示,简而言之,每次选取未曾被连接顶点前提下是最小权值的线。
最短路径
迪杰斯特拉(Dijkstra)算法是求单源点最短路径的算法,是给定带权有向图G和源点v0到G的各个顶点的最短路径。
思想:把网中所有的顶点化为两个集合S和T,T集合的初态只有v0一个顶点,S集合的初态为除了v0之外的所有顶点。凡是以v0为源点,已经确定了最短路径的终点最终并入S集合中,顶点集合T则是尚未确定最短路径的顶点集合。按照各顶点与v0最短路径长度递增的次序,逐个把T集合中的顶点加入到S集合中去,使得v0到S集合中各个顶点路径的长度适中不大于从v0到T集合中各个顶点的长度。