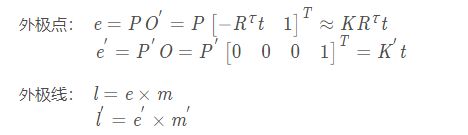计算机视觉——多视图几何

一、基本原理

1.1外极几何

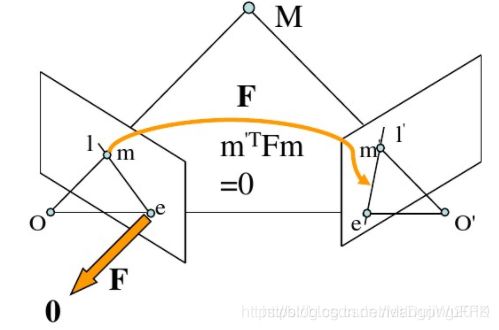
外极几何是研究两幅图像之间存在的几何。它和场景结构无关，只依赖于摄像机的内外参数。研究这种几何可以用在图像匹配、三维重建方面。

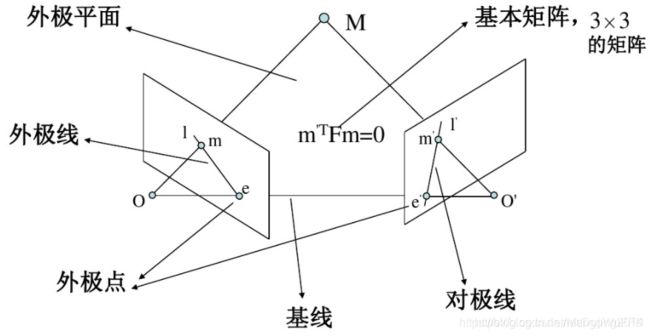
外极点： 基线与像平面的交点。
外极平面： 过基线的平面。
外极线： 对极平面与图像平面的交线。
基本矩阵F ： 对应点对之间的约束m’Fm=0

基础矩阵的代数推导：

1.2基础矩阵的估算方法

基础矩阵F是一个3×3的矩阵，有9个未知元素。然而，上面的公式中使用的齐次坐标，齐次坐标在相差一个常数因子下是相等，F也就只有8个未知元素，也就是说，只需要8对匹配的点对就可以求解出两视图的基础矩阵F FF。
假设在两幅图像对应匹配点的坐标分别为：
由基础矩阵公式得

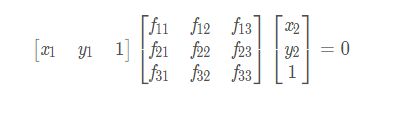
也即：

将上述公式中的F看成列向量：

那么可将上述公式改写为：
给定8组点的集合，我们有如下方程：

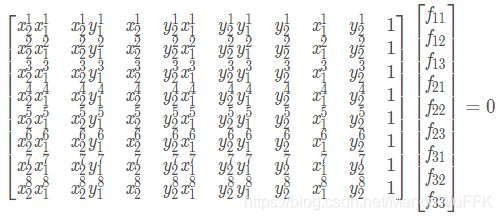
求解上面的方程组就可以得到基础矩阵各个元素了。

八点法 优点: 线性求解，容易实现，运行速度快 . 缺点：对噪声敏感

最小二乘法估算
使用归一化的坐标虽然能够在一定程度上消除噪声、错误匹配带来的影响，但还是不够的。8点法中，只使用8对匹配的点对估计基础矩阵，但通常两幅图像的匹配的点对远远多于8对，可以利用更多匹配的点对来求解上面的方程。

由于基础矩阵F在一个常量因子下是等价的，这样可以给基础矩阵F的元素组成的向量f施加一个约束条件


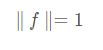
可以对矩阵Q 进行奇异值分解（SVD）


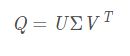
在估计基础矩阵时，设其最小奇异值为0，对上面方法取得的基础矩阵进行SVD分解

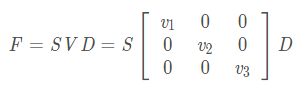
其最小特征值v3被设为0，以使得F的秩为2.这样得到

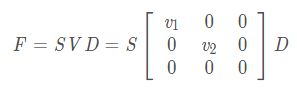
上述F就是最终得到的基础矩阵。

二、实验内容和分析

2.1实验内容

1.求解图像之间的基础矩阵
要求：分别用七点、八点、十点（匹配点），计算基础矩阵

2.实验图片包含三种情况，即（1）左右拍摄，极点位于图像平面上（2）像平面接近平行，极点位于无穷远（3）图像拍摄位置位于前后
针对上述情况，画出极点和极线，其中点坐标要均匀分布于各行

2.2 求解图像之间的基础矩阵

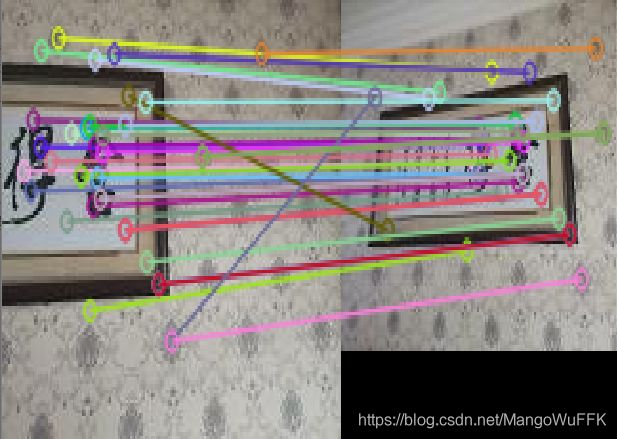
1.匹配点为七点
SIFT匹配

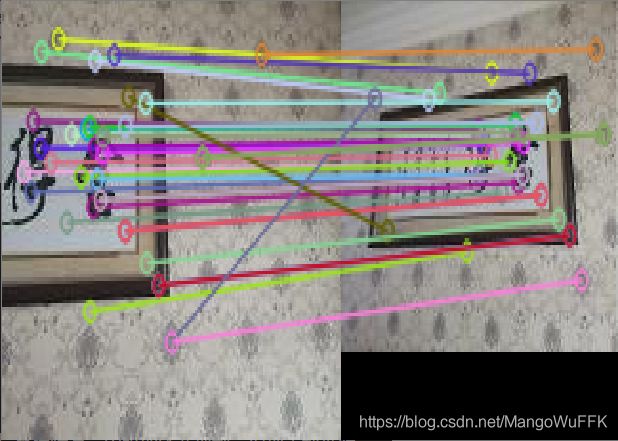
RANSAC筛选

基础矩阵：
[[-3.74405115e-04 2.97061956e-04 2.10048565e-02]
[ 5.22267792e-04 -3.91300262e-04 -3.06613580e-02]
[-1.48410971e-02 8.93704635e-03 1.00000000e+00]]

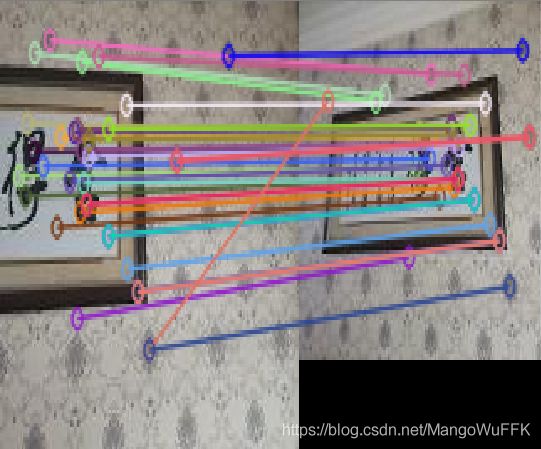
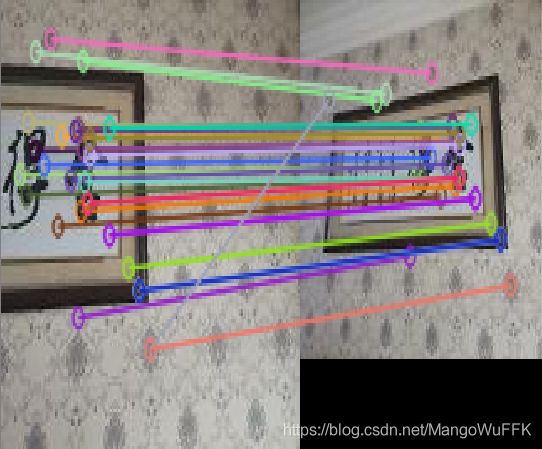
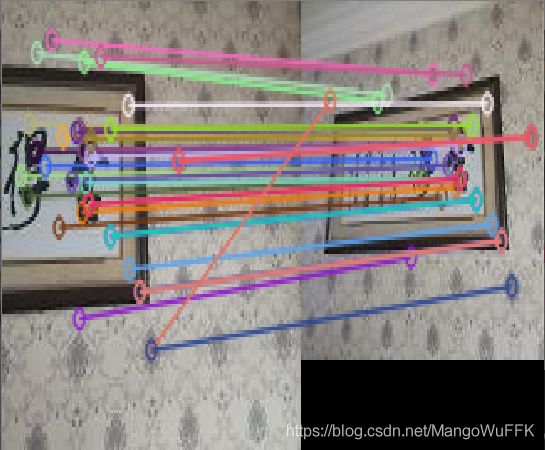
2.匹配点为八点
SIFT匹配

RANSAC筛选

基础矩阵
[[-2.69636313e-04 -9.17789259e-04 -2.95714666e-02]
[ 8.15264237e-04 1.01311622e-03 6.46453229e-02]
[ 8.17746079e-02 -2.88532391e-01 1.00000000e+00]]

3.匹配点为十点
SIFT匹配后

RANSAC筛选后

基础矩阵：
[[-1.35563615e-04 -4.72508953e-04 2.21439541e-03]
[ 5.46455880e-04 2.37112976e-04 5.28351729e-03]
[ 1.62115556e-02 -9.19249361e-02 1.00000000e+00]]

小结：
正如8点算法一样，使用7个点对应可得到以下方程：

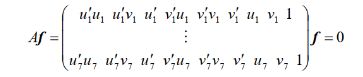
若图像中仅有7个对应点，当基本矩阵有3个解时，不能断定哪-一个是真解。如果图像中有多于7个点对应，当基本矩阵有3个解时，可选取匹配点对应数最多的矩阵作为基本矩阵的真解。

参考：https://www.jiqizhixin.com/articles/19052902 谭平教授

1.当得到1个实数解、2个虚数解时，直接舍弃虚数解，实数解就是F的唯一 解;

2.当得到3个实数解时，称之为critical condition,这意味着，F的7个点和两个相机中心点，这9个点，通过三维空间中某个特定曲面。在这种特定情况下，7个对应点不能唯一确定一个F。

3.而匹配点大于等于8点时，对基础矩阵并无太大的影响。

2.3代码

def compute_fundamental(x1, x2):
   n = x1.shape[1]
   if x2.shape[1] != n:
       raise ValueError("Number of points don't match.")
   A = np.zeros((n, 9))
   for i in range(n):
       A[i] = [x1[0, i] * x2[0, i], x1[0, i] * x2[1, i], x1[0, i] * x2[2, i],
               x1[1, i] * x2[0, i], x1[1, i] * x2[1, i], x1[1, i] * x2[2, i],
               x1[2, i] * x2[0, i], x1[2, i] * x2[1, i], x1[2, i] * x2[2, i]]
   U, S, V = np.linalg.svd(A)
   F = V[-1].reshape(3, 3)
   U, S, V = np.linalg.svd(F)
   S[2] = 0
   F = np.dot(U, np.dot(np.diag(S), V))

   return F / F[2, 2]

将匹配点进行归一化处理

 def compute_fundamental_normalized(x1, x2):
    n = x1.shape[1]
    if x2.shape[1] != n:
        raise ValueError("Number of points don't match.")
    # normalize image coordinates
    x1 = x1 / x1[2]
    mean_1 = np.mean(x1[:2], axis=1)
    S1 = np.sqrt(2) / np.std(x1[:2])
    T1 = np.array([[S1, 0, -S1 * mean_1[0]], [0, S1, -S1 * mean_1[1]], [0, 0, 1]])
    x1 = np.dot(T1, x1)
    x2 = x2 / x2[2]
    mean_2 = np.mean(x2[:2], axis=1)
    S2 = np.sqrt(2) / np.std(x2[:2])
    T2 = np.array([[S2, 0, -S2 * mean_2[0]], [0, S2, -S2 * mean_2[1]], [0, 0, 1]])
    x2 = np.dot(T2, x2)
   
    # compute F with the normalized coordinates
    F = compute_fundamental(x1, x2)
    # print (F)
    # reverse normalization
    F = np.dot(T1.T, np.dot(F, T2))

    return F / F[2, 2]

随机选择几对匹配点，用于计算基础矩阵

def randSeed(good, num = 8):
 '''
 :param good: 初始的匹配点对
 :param num: 选择随机选取的点对数量
 :return: 8个点对list
 '''
 eight_point = random.sample(good, num)
 return eight_point

因为是三维的，所以此处增加了一个维度使得返回的为(x,y,1) (x,y,1)(x,y,1)的形式，与前述公式对应。

def PointCoordinates(eight_points, keypoints1, keypoints2):
    '''
    :param eight_points: 随机八点
    :param keypoints1: 点坐标
    :param keypoints2: 点坐标
    :return:8个点
    '''
    x1 = []
    x2 = []
    tuple_dim = (1.,)
    for i in eight_points:
        tuple_x1 = keypoints1[i[0].queryIdx].pt + tuple_dim
        tuple_x2 = keypoints2[i[0].trainIdx].pt + tuple_dim
        x1.append(tuple_x1)
        x2.append(tuple_x2)
    return np.array(x1, dtype=float), np.array(x2, dtype=float)

2.4 针对上述情况，画出极点和极线，其中点坐标要均匀分布于各行

1.左右拍摄，极点位于图像平面上
1.1室外景深丰富

1.2室内景深丰富

1.3室内景深单一

小结：
无论是室内，室外还是景深复杂与单一，左右拍摄的情况下，极限位于平面上，且每条极限都会交于一个点上，而且极限普遍较少。且极线方向各异没有全部都是平行的。
2.像平面接近平行，极点位于无穷远
2.1室内平面平行

2.2室外平面平行

小结：
无论是室内还是室外，每张图的极限都是每条平行向着一个方向，因为平面平行拍摄极点在无穷远处，所以才会变成这样的情况。

2.3图像拍摄位置位于前后

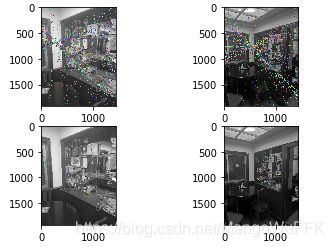
小结：
在采用课本的代码时，对于图像拍摄位置位于前后，无论是室内还是室外，也不受灯光影响，

基本都因为特征点过少而出现这类错误，所以换代码。前后拍摄的话，所有极线都是汇聚在远端的一点上。

2.5代码

print(F)

e = sfm.compute_epipole(F)
# 绘制图像
figure()
imshow(im1)
# 分别绘制每条线，这样会绘制出很漂亮的颜色
for i in range(5):
    sfm.plot_epipolar_line(im1,F,x2[:,i],e,False)
axis('off')
figure()
imshow(im2)
print(len(x2))
# 分别绘制每个点，这样会绘制出和线同样的颜色
for i in range(5):
    plot(x2[0,i],x2[1,i],'o')
axis('off')
show()

三、错误解决

1.
解决方法：

2.

解决方法：