#简单线性回归的程序
import numpy as np
#应该导入的类
from sklearn.linear_model import LinearRegression
#用来切割训练集和测试集的类
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
#设置输出的进度::默认是8
np.set_printoptions(precision=2)
iris = load_iris()
#获取花瓣长度作为X,而花瓣宽度作为y
X,y = iris.data[:, 2].reshape(-1,1), iris.data[:,3]#X有一个转置
#将数据集划分为训练集与测试集:test_size:测试集的大小,random_state:随机种子用来产生相同的随机数序列
lr = LinearRegression()
#定义不同变量以区分
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size= 0.25,random_state = 0)
#使用训练集数据,训练模型。
lr.fit(X_train,y_train)#真的很方便,很容易看懂。别再转牛角尖
print('权重:', lr.coef_)
print('截距:', lr.intercept_)
#从训练集学习到了模型的参数(w,b),确定方程,就可以进行预测。
y_hat = lr.predict(X_test)
print("实际值", y_test)
print("预测值", y_hat)
y_hat1 = X_test * lr.coef_ + lr.intercept_
print(type(X_test))
y_hat1.reshape(1,38)

#将预测模型可视化
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = "simsun"
plt.rcParams["axes.unicode_minus"] = False
plt.rcParams["font.size"] = 15
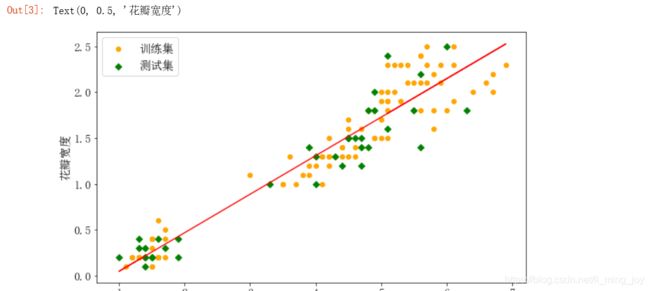
plt.figure(figsize=(10,6))
plt.scatter(X_train,y_train,c='orange',label='训练集')
plt.scatter(X_test,y_test,c='g',marker='D',label='测试集')
plt.plot(X,lr.predict(X),'r-')
plt.legend()
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
plt.figure(figsize = (15,6))
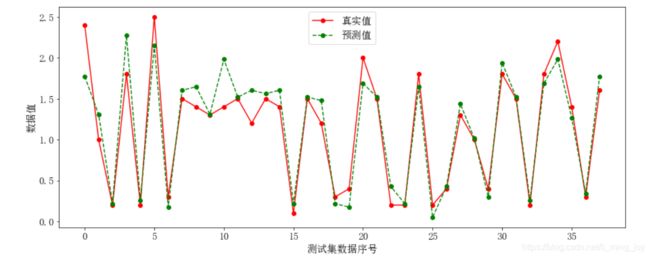
plt.plot(y_test,label='真实值',color='r',marker='o')
plt.plot(y_hat,label='预测值',ls='--',color='g',marker='o')
plt.xlabel('测试集数据序号')
plt.ylabel('数据值')
plt.legend()
#回归模型的评估:已经建立的模型准确度到底怎么样呢?
#这里有四个常用的指标可以进行衡量
#他们分别是:MSE(MEAN SQUARED ERROR平均平方误差),RMSE(ROOT...)
#最常用R方
#各项指标一测
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
print('均方误差(MSE)',mean_squared_error(y_test, y_hat))
print('根均方误差(RMSE)',np.sqrt(mean_squared_error(y_test,y_hat)))
print('平均绝对值误差(MAE)',mean_absolute_error(y_test,y_hat))
print('训练集R²',r2_score(y_train,lr.predict(X_train)))
print('测试集R²',r2_score(y_test,y_hat))
#score其实求解的就是r²的值,但是它与r2_score方法所用到的方法传参不同
print('训练集R²',lr.score(X_train,y_train))
print('测试集R²',lr.score(X_test,y_test))

#波士顿房价的多元线性回归实例
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
import pandas as pd
boston = load_boston()
X,y = boston.data, boston.target
df = pd.DataFrame(np.concatenate([X,y.reshape(-1,1)],axis = 1),columns = boston.feature_names.tolist() + ['MEDV'])
df.head()
X_train,X_test,y_train,y_test = train_test_split(
X,y,test_size = 0.25,random_state = 0)
lr = LinearRegression()
lr.fit(X_train,y_train)
print('模型权重',lr.coef_)
print('截距',lr.intercept_)
y_hat = lr.predict(X_test)
print('训练集R²',lr.score(X_train,y_train))
print('测试集R²',lr.score(X_test,y_test))





