分治应用--最近点对问题 & POJ 3714

1. 问题描述

二维平面上有n个点，如何快速计算出两个距离最近的点对？

2. 解题思路

• 暴力做法是，每个点与其他点去计算距离，取最小的出来，复杂度O(n²)
• 采用分治算法

1. 将数据点按照 x 坐标排序，找到中位点，过中位点划线 x = mid_x 将数据分成2部分，递归划分，直到两个半边只有1个或者2个数据，只有1个数据点，最短距离返回无穷大，有2个点直接返回2点的距离
2. 合并左右两边的结果，取左右两边的最短距离的较小值为 d = min{dl,dr}，那么在 x = mid_x 的 ± d 范围内的左右点对才有可能距离比 d 更小（好理解）
3. 对这个范围内的点，再按照 y 坐标排序，查找两个点的 y 差值小于 d 的点对（重点在这里，见下面分析），计算其距离是否比 d 更小
   
   假如在这个范围内的有1,2,3,4,5,6六个点（按 y 坐标排序），寻找距离小于 d 的点对，如果暴力查找，复杂度还是 n²，我们可以看出点4只有可能在其上下y坐标 ± d 的范围内找到满足距离小于 d 的点匹配，点1和点4不可能距离小于 d，左边的点最多可以有4个右边的点使得其距离小于 d
   
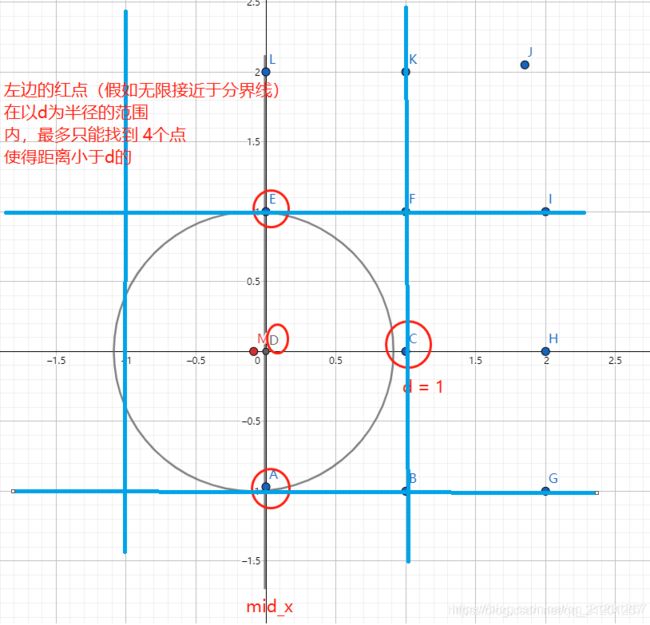
   所以，步骤3是O（n）复杂度。
   T(1) = 1；T(n) = 2*T(n/2)+n；高中数学即可求得T(n)是O(nlogn)的复杂度。

3. 实现代码

/**
 * @description: 2维平面寻找距离最近的点对（分治）
 * @author: michael ming
 * @date: 2019/7/4 23:16
 * @modified by: 
 */
#include 
#include 
#include 
#include 
#include 
#define LEFT_BOUND 0.0
#define RIGHT_BOUND 100.0
#define LOWER_BOUND 0.0
#define UPPER_BOUND 100.0   //随机点的范围
using namespace std;
class Point//点
{
public:
    int id;
    double x, y;
    Point(int index, double x0, double y0):id(index),x(x0),y(y0){}
};
typedef vector<Point> PointVec;
bool compx(const Point &a, const Point &b)
{
    if(a.x != b.x)
        return a.x < b.x;
    return a.y < b.y;
}
bool compy(const Point &a, const Point &b)
{
    return a.y < b.y;
}

class ClosestPoint
{
    PointVec points_vec;
    int numOfPoint;
public:
    ClosestPoint()
    {
        srand(unsigned(time(0)));
        double x, y;
        cout << "请输入测试点个数，将随机生成散点：";
        cin >> numOfPoint;
        for(int i = 0; i < numOfPoint; ++i)
        {
            x = LEFT_BOUND + (double)rand()/RAND_MAX *(RIGHT_BOUND-LEFT_BOUND);
            y = LOWER_BOUND + (double)rand()/RAND_MAX *(UPPER_BOUND-LOWER_BOUND);
            cout << i+1 << " (" << x << "," << y << ")" << endl;
            points_vec.emplace_back(i+1,x,y);//生成点的动态数组
        }
    }

    double dist(const Point &a, const Point &b)
    {
        double dx = a.x - b.x;
        double dy = a.y - b.y;
        return sqrt(dx*dx + dy*dy);//返回两点之间的距离
    }
    void bfCalDist()//暴力求解
    {
        size_t num = points_vec.size();
        if(num <= 1)
        {
            cout << "输入个数<=1 !!!" << endl;
            return;
        }
        int i, j, s, t;
        double distance = RAND_MAX, d;
        for(i = 0; i < num; ++i)
            for(j = i+1; j < num; ++j)
            {
                d = dist(points_vec[i], points_vec[j]);
                if(d < distance)
                {
                    distance = d;
                    s = points_vec[i].id;
                    t = points_vec[j].id;
                }
            }
        cout << "点" << s << "到点" << t << "的距离最小：" << distance << endl;
    }
    double calcDist(size_t left, size_t right, size_t &s, size_t &t)
    {
        if(left == right)//一个点,返回无穷大
            return RAND_MAX;
        if(left+1 == right)//两个点，直接计算距离
        {
            s = points_vec[left].id;
            t = points_vec[right].id;
            return dist(points_vec[left],points_vec[right]);
        }
        sort(points_vec.begin()+left,points_vec.begin()+right+1,compx);
        //把点群按照x排序
        size_t mid = (left+right)/2;
        double mid_x = points_vec[mid].x;
        double distance = RAND_MAX, d;
        distance = min(distance,calcDist(left,mid,s,t));//递归划分左边
        distance = min(distance,calcDist(mid+1,right,s,t));//递归划分右边
        size_t i, j, k = 0;
        PointVec temp;//存储临时点（在mid_x左右d范围内的）
        for(i = left; i <= right; ++i)
        {
            if(fabs(points_vec[i].x-mid_x) <= distance)
            {
                temp.emplace_back(points_vec[i].id,points_vec[i].x,points_vec[i].y);
                k++;
            }
        }
        sort(temp.begin(),temp.end(),compy);//再把范围内的点，按y排序
        for(i = 0; i < k; ++i)
        {
            for(j = i+1; j < k && temp[j].y-temp[i].y < distance; ++j)
            {//在临时点里寻找距离更小的，内层循环最多执行不超过4次就会退出
                d = dist(temp[i],temp[j]);
                if(d < distance)
                {
                    distance = d;
                    s = temp[i].id;
                    t = temp[j].id;
                }
            }
        }
        return distance;
    }
    void closestDist()//调用分治求解
    {
        size_t num = points_vec.size();
        if(num <= 1)
        {
            cout << "输入个数<=1 !!!" << endl;
            return;
        }
        size_t s, t; s = t = 0;//记录起终点
        double d = calcDist(0,num-1,s,t);
        cout << "点" << s << "到点" << t << "的距离最小：" << d << endl;
    }

};
int main()
{
    ClosestPoint cp;
    clock_t start, end;
    cout << "方法1，暴力求解：" << endl;
    start = clock();
    cp.bfCalDist();
    end = clock();
    cout << "耗时：" << (double)(end - start) << "ms." << endl;
    cout << "-------------------" << endl;
    cout << "方法2，分治求解：" << endl;
    start = clock();
    cp.closestDist();
    end = clock();
    cout << "耗时：" << (double)(end - start) << "ms." << endl;
    return 0;
}

4. POJ 3714

http://poj.org/problem?id=3714
相同的问题，只是数据位置分为2类（人，核电站），计算距离时，需判断是不同的类，否则返回一个很大的数。

以下代码显示Wrong Answer，谁帮忙看下。测试样例输出是一样的。

/**
 * @description: poj3714求解最近的核电站距离
 * @author: michael ming
 * @date: 2019/7/6 0:09
 * @modified by: 
 */
#include
#include 
#include 
#include 
#include 
#define DBL_MAX 1.7976931348623158e+308
using namespace std;
class Point//点
{
public:
    int id;
    int x, y;
    Point(int index, int x0, int y0):id(index),x(x0),y(y0){}
};
typedef vector<Point> PointVec;
bool compx(const Point &a, const Point &b)
{
    if(a.x != b.x)
        return a.x < b.x;
    return a.y < b.y;
}
bool compy(const Point &a, const Point &b)
{
    return a.y < b.y;
}

class ClosestPoint
{
    PointVec points_vec;
    int numOfPoint;
public:
    ClosestPoint()
    {
        int x, y;
        cin >> numOfPoint;
        for(int i = 0; i < numOfPoint; ++i)
        {
            cin >> x >> y;
            points_vec.push_back(Point(0,x,y));//生成站点的动态数组（0表示站）
        }
        for(int i = 0; i < numOfPoint; ++i)
        {
            cin >> x >> y;
            points_vec.push_back(Point(1,x,y));//加入人的位置（1表示人）
        }
    }

    double dist(const Point &a, const Point &b)
    {
        if(a.id == b.id)
            return DBL_MAX;//相同的类型，返回很大的数
        int dx = a.x - b.x;
        int dy = a.y - b.y;
        return sqrt(double(dx*dx + dy*dy));//返回两点之间的距离
    }

    double calcDist(size_t left, size_t right)
    {
        if(left == right)//一个点,返回无穷大
            return DBL_MAX;
        if(left+1 == right)//两个点，直接计算距离
        {
            return dist(points_vec[left],points_vec[right]);
        }
        sort(points_vec.begin()+left,points_vec.begin()+right+1,compx);
        //把点群按照x排序
        size_t mid = (left+right)/2;
        double mid_x = points_vec[mid].x;
        double distance = DBL_MAX, d;
        distance = min(distance,calcDist(left,mid));//递归划分左边
        distance = min(distance,calcDist(mid+1,right));//递归划分右边
        size_t i, j, k = 0;
        PointVec temp;//存储临时点（在mid_x左右d范围内的）
        for(i = left; i <= right; ++i)
        {
            if(fabs(points_vec[i].x-mid_x) <= distance)
            {
                temp.push_back(Point(points_vec[i].id,points_vec[i].x,points_vec[i].y));
                k++;
            }
        }
        sort(temp.begin(),temp.end(),compy);//再把范围内的点，按y排序
        for(i = 0; i < k; ++i)
        {
            for(j = i+1; j < k && temp[j].y-temp[i].y <= distance; ++j)
            {//在临时点里寻找距离更小的，内层循环最多执行不超过4次就会退出
                d = dist(temp[i],temp[j]);
                if(d < distance)
                {
                    distance = d;
                }
            }
        }
        return distance;
    }
    double closestDist()//调用分治求解
    {
        size_t num = points_vec.size();
        return calcDist(0,num-1);
    }

};
int main()
{
    int times;
    cin >> times;
    while (times--)
    {
        ClosestPoint cp;
        cout << fixed << setprecision(3) << cp.closestDist() << endl;
    }
    return 0;
}