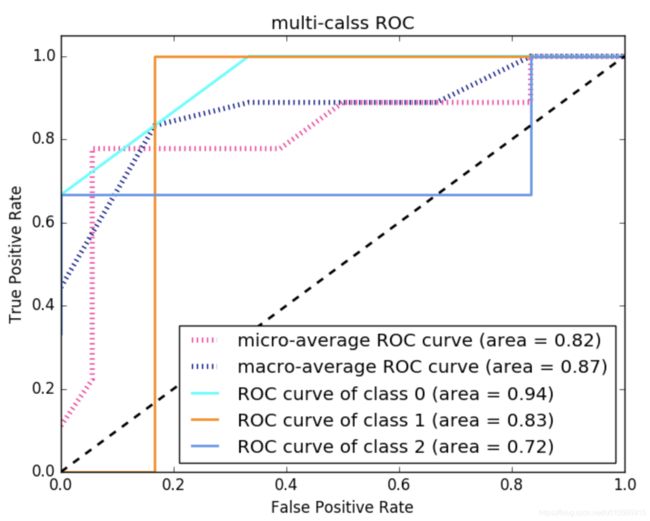
多分类ROC曲线及AUC计算
上一篇博客(https://blog.csdn.net/u010505915/article/details/106394765)介绍了二分类下的ROC曲线及AUC计算,本文主要介绍多分类下的ROC曲线及AUC计算。
对于多分类数据,假设测试样本个数为m,分类个数为n(分类label分别为:1,2,...,n),可以将这些样本及对应的label表示为矩阵形式,每行一个样本,每列为该样本是否属于该分类,从而形成一个[m, n]的标签矩阵:
| ID | 分类1 | 分类2 | 分类3 |
| A | 1 | 0 | 0 |
| B | 0 | 0 | 1 |
| C | 0 | 1 | 0 |
| D | 0 | 0 | 1 |
模型预测完成后,会计算出测试样本在各个分类下的概率,模型预测得分也能用一个[m, n]的矩阵表示,每一行表示样本在各个类别下的概率,记该矩阵为P。
| ID | 分类1 | 分类2 | 分类3 |
| A | 0.8 | 0.15 | 0.05 |
| B | 0.2 | 0.3 | 0.5 |
| C | 0.3 | 0.6 | 0.1 |
| D | 0.2 | 0.1 | 0.7 |
多分类下画ROC曲线有两种方法:
方法1:对每种类别,都可以从矩阵P中得到m个测试样本在该分类下的打分(矩阵P中的列),从矩阵L中获取样本的类别,从而形成一个类似二分类的得分矩阵,以上图为例,分类1 的矩阵为:
| ID | label | score |
| A | 1 | 0.8 |
| B | 0 | 0.2 |
| C | 0 | 0.3 |
| D | 0 | 0.2 |
按二分类中画ROC曲线的方法,根据以上矩阵,可以计算出各个阈值下的假正例率(FPR)和真正例率(TPR),从而画出一条ROC曲线。
对每一个类别,可以画出一条ROC曲线,总共可以画出n条ROC曲线。最后对这n条ROC曲线取平均值,即可得到最终的ROC曲线。
在python中,该方法对于sklearn里sklearn.metrics.roc_auc_score函数中参数average值为'macro'的情况。
方法2:对于一个测试样本:
(1)标签由0和1组成,1的位置表明了它的类别,0表示其他类别。1对应二分类问题中的“正”,0对应“负”
(2)如果模型对该样本分类正确,则该样本在标签矩阵L中1对应的位置在概率矩阵P中的值,即为模型预测该分类的概率值。
基于以上两点,将标签矩阵L和概率矩阵P分别按行展开(即sklearn里的ravel()函数),然后转置形成两列,这就得到了一个二分类结果,根据结果直接画出ROC曲线。
在python中,该方法对于sklearn里sklearn.metrics.roc_auc_score函数中参数average值为'micro'的情况。
代码示例:
#-*-coding:utf-8-*-
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
from sklearn.metrics import roc_curve, auc
from scipy import interp
y_label = np.array([
[1, 0, 0], [1, 0, 0], [1, 0, 0],
[0, 1, 0], [0, 1, 0], [0, 1, 0],
[0, 0, 1], [0, 0, 1], [0, 0, 1]
])
y_score = np.array([
[0.8, 0.1, 0.1], [0.2, 0.32, 0.48], [0.6, 0.1, 0.3],
[0.2, 0.5, 0.3], [0.1, 0.6, 0.3], [0.2, 0.75, 0.05],
[0.05, 0.05, 0.9], [0.1, 0.3, 0.6], [0.12, 0.8, 0.08],
])
n_classes = 3
# 计算每一类的ROC
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_label[:, i], y_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# micro(方法二)
fpr["micro"], tpr["micro"], _ = roc_curve(y_label.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
# macro(方法一)
# First aggregate all false positive rates
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))
# Then interpolate all ROC curves at this points
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
mean_tpr += interp(all_fpr, fpr[i], tpr[i])
# Finally average it and compute AUC
mean_tpr /= n_classes
fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
# Plot all ROC curves
lw=2
plt.figure()
plt.plot(fpr["micro"], tpr["micro"],
label='micro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["micro"]),
color='deeppink', linestyle=':', linewidth=4)
plt.plot(fpr["macro"], tpr["macro"],
label='macro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["macro"]),
color='navy', linestyle=':', linewidth=4)
colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(n_classes), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=lw,
label='ROC curve of class {0} (area = {1:0.2f})'
''.format(i, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('multi-calss ROC')
plt.legend(loc="lower right")
plt.show()ROC曲线:
参考文献:
https://blog.csdn.net/u011047955/article/details/87259052