时间序列预测模型笔记

时间序列预测模型有四种：AR、MA、ARMA和ARIMA模型。本文首先介绍四种模型的含义及对比，然后详细介绍ARIMA模型实现步骤。

一、四种模型含义及对比

1、AR、MA、ARMA和ARIMA模型

AR可以解决当前数据与后期数据之间的关系，MA则可以解决随机变动也就是噪声的问题。ARMA模型是与自回归和移动平均模型两部分组成。所以可以表示为ARMA(p, q)。p是自回归阶数，q是移动平均阶数。



注意，采用ARIMA模型预测时序数据，必须是稳定的，如果不稳定的数据，是无法捕捉到规律的。比如股票数据用ARIMA无法预测的原因就是股票数据是非稳定的，常常受政策和新闻的影响而波动。

二、ARIMA模型实现步骤

1）获取时间序列数据

2）检查序列是否为平稳非白噪声时间序列
检验平稳性方法：绘图观察、ADF单位根平稳型检验

对于不平稳的序列，可做**d阶**差分运算，或者取对数操作。

检验白噪声方法：
statsmodels 库acorr_ljungbox方法

3）通过第二步的处理，得到平稳的时间序列。通过平稳的时间序列，求最佳**p和q**。

实际编码中，可通过遍历p、q，取使得Bic值最小的方法求得。

4）由以上得到的d、q、p ，得到ARIMA模型。然后对模型进行检验和优化。最后运用最终模型进行预测。

预测方法：predict函数和forecast函数。

三、相关基础概念

1、差分
用现在的观测值减去上一个时刻值就可得到差分结果。
差分的原因：降低时间对数据的影响。
滞后差分：连续观测值之间的差分变换叫做一阶滞后差分。滞后差分的步长根据时间结果做调整。

如何利用python 对数据进行差分：numpy diff函数**

参数：

a：输入矩阵

n：可选，代表要执行几次差值

axis：默认是最后一个

示例：

import numpy as np     

A = np.arange(2 , 14).reshape((3 , 4))    
   
A[1 , 1] = 8    
   
print('A:' , A)

 #  A: [[ 2  3  4  5]
      
#       [ 6  8   8  9]

#       [10 11 12 13]]
   

print(np.diff(A))

# [[1 1 1]
#  [2 0 1]
#  [1 1 1]]

从输出结果可以看出，其实diff函数就是执行的是后一个元素减去前一个元素。

参考：https://blog.csdn.net/hanshuobest/article/details/78558826
如何利用python 对数据进行差分： http://www.360doc.com/content/17/0605/12/42308479_660150397.shtml

其他差分方法
https://blog.csdn.net/tmb8z9vdm66wh68vx1/article/details/84207895

2、adf检验**
含义：
adf检验就是单位根检验。
指检验序列中是否存在单位根，因为存在单位根就是非平稳时间序列了。单位根就是指单位根过程，可以证明，序列中存在单位根过程就不平稳，会使回归分析中存在伪回归。

ADF原假设为，序列存在单位根，即非平稳，对于一个平稳的时序数据，就需要在给定的置信水平上显著，拒绝原假设。

ADF结果查看方法，有两种：
1、若得到的统计量显著小于3个置信度（1%，5%，10%）的临界统计值时，说明是拒绝原假设的。即：查看统计量的值，若统计量的值都小于3个置信度的值，则说明序列平稳。

2、另外是看P-value是否非常接近0.（4位小数基本即可）
查看adf检验结果P-value：
值要求小于给定的显著性水平,一般是0.05、0.01等,p越接近于0越好；

例如，一个adf检验结果如下:

adf 结果： (-7.703453304753249, 1.3205161280050353e-11, 0, 84, {'1%': -3.510711795769895, '5%': -2.8966159448223734, '10%': -2.5854823866213152}, 520.0070353452603)

第一个值-7.703453304753249：ADF Test result（即统计量）
第二个值1.3205161280050353e-11：P-Value
第三部分{‘1%’: -3.510711795769895, ‘5%’: -2.8966159448223734, ‘10%’: -2.5854823866213152}:三个程度下拒绝原假设的统计值

那么，此序列是否平稳呢？可以从两个方面看出：
1、ADF Test result明显小于第三部分3个值，可以判定其为平稳的。
2、P-Value为1e-11，很接近于0，可以判定此序列为平稳的。

其实在第1点中，若是看到ADF Test result已经小于1%统计量的值，就可显著的拒绝原假设（数据非平稳），认为数据平稳。
对于ADF结果在1% 以上 5%以下的结果，也不能说不平稳，关键看检验要求是什么样子的。

如何在python中做adf检验呢？
可通过statsmodels.tsa.stattools.adfuller函数进行adf校验。例如有一个时间序列day_max，则对其进行单位根检验可用如下语句：

 print("adf 结果：",str(adfuller(day_max)))

得出的结果就是上例中的结果。

参考链接：Python时间序列中ADF检验详解 ：https://blog.csdn.net/weixin_42382211/article/details/81332431

参考：
时间序列分析之AR、MA、ARMA和ARIMA模型：https://blog.csdn.net/FrankieHello/article/details/80883147
时间序列预测之–ARIMA模型：https://www.cnblogs.com/bradleon/p/6827109.html

3、什么是残差？残差序列？白噪声？白噪声检验方法？

残差：预测值减去真实值，即为残差。所有预测值序列减去真实值序列，即为残差序列。

什么是白噪声检验？

白噪声是一种特殊的弱平稳过程，通常时间序列分析到白噪声这一层就没什么好分析的了。
做时间序列分析，之前需要做两个准备工作，即检查序列是否是平稳的，如果是平稳的，还要检查是否是白噪声。

对残差序列进行白噪声检验，若残差序列是白噪声，则说明原始序列中已经没有什么可提取的价值了。
python中如何进行白噪声检验？

#导入acorr_ljungbox库          
from statsmodels.stats.diagnostic import acorr_ljungbox          
#检验。其中参数D_df是一个差分序列，dataframe类型          
print("差分序列的白噪声检验结果：" +str(acorr_ljungbox(D_df, lags= 1)))   

输出如下：

差分序列的白噪声检验结果：(array([16.3875593]), array([5.16229461e-05]))

第一个值是统计量，第二个值是P-value。ljungbox检验的原假设，时间序列是一个白噪声。若p-value小于0.05，则可以拒绝原假设，证明原序列非白噪声。若大于0.05，则不能拒绝原假设，原序列是一个白噪声。很明显，上述结果显示，该序列非白噪声，可以继续进行时间序列建模。

参考：时间序列经过差分后变成了白噪声，还如何利用ARIMA建模？http://www.dataguru.cn/thread-639947-1-1.html

4、p、q值的确定

两种方法：

1、根据自相关，偏自相关图初步确定p,q。

2、取一个p、q的上限值，一般是小于10，然后遍历取所有p、q组合，分别求bic值，使bic值最小的p、q值即为最终的p、q。

p,q值确定，即可得到ARIMA模型了。

具体实现代码如下：

from statsmodels.tsa.arima_model import ARIMA

#定阶
pmax = int(len(xdata)/10) #一般阶数不超过length/10
qmax = int(len(xdata)/10) #一般阶数不超过length/10
bic_matrix = [] #bic矩阵
for p in range(pmax+1):
  tmp = []
  for q in range(qmax+1):
    try: #存在部分报错，所以用try来跳过报错。
      tmp.append(ARIMA(xdata, (p,1,q)).fit().bic)
    except:
      tmp.append(None)
  bic_matrix.append(tmp)
print(bic_matrix)
#[[1275.6868239439104, 1273.190434524266, 1273.5749982328914, 1274.4669152438114, None], 
#[1276.7491283595593, 1271.8999324285992, None, None, None], 
#[1279.6942963992901, 1277.5553412371614, None, 1280.0924824267408, None],
# [1278.0659994468958, 1278.9885944429066, 1282.782534558853, 1285.943493708969, None], [1281.220790614283, 1282.6999920212124, 1286.2975191780365, 1290.1950373803218, None]]
bic_matrix = pd.DataFrame(bic_matrix) #从中可以找出最小值
print(bic_matrix)
        0            1            2            3     4
 0  1275.686824  1273.190435  1273.574998  1274.466915  None
 1  1276.749128  1271.899932          NaN          NaN  None
 2  1279.694296  1277.555341          NaN  1280.092482  None
 3  1278.065999  1278.988594  1282.782535  1285.943494  None
 4  1281.220791  1282.699992  1286.297519  1290.195037  None
print(bic_matrix.stack())
 0  0    1275.69
    1    1273.19
    2    1273.57
    3    1274.47
 1  0    1276.75
    1     1271.9
 2  0    1279.69
    1    1277.56
    3    1280.09
 3  0    1278.07
    1    1278.99
    2    1282.78
    3    1285.94
4  0     1281.22
   1     282.7
   2     1286.3
   3     1290.2
p,q = bic_matrix.stack().astype('float64').idxmin() #先用stack展平，然后用idxmin找出最小值位置。
print(u'BIC最小的p值和q值为：%s、%s' %(p,q))
参考：ARIMA模型识别、计算p、q值：https://www.cnblogs.com/ggzhangxiaochao/p/9122619.html

5、模型预测
ARIMA模型进

行预测。预测的方法有两种，一种是用predict函数，一种是用forecast函数。Predict函数只能对原数据进行预测，forecast函数可对未来数据进行单步或多步预测。

predict函数的dynamic参数为True表示对未知数据进行预测，false表示对原数据预测。
样本内预测：利用模型对训练数据进行预测，可将训练数据实际值和预测值做一个对比。
样本外预测：利用训练出的模型对未来的数据进行预测。

样本外预测的话，ARIMA模型只适合短期预测。长期的话你还是看看时间序列的趋势预测。预测的时间特别长的话，只能用传统的时间序列的乘法模型。预测还是不要看趋势，如果是个指数模型，你拟合成线性的肯定误差大。一般误差在5%以内就差不多了。数据多，模型合适，误差可以在1%内。

ARIMA模型适合做稳定时间序列的预测，非稳定数据，例如股票、期货之类的预测，auto.arima就不合适了。
一般取对数后，趋势就小很多。经过季节性差分（差分步长是季节周期的长度）就可以消除季节性影响。

预测的最长期数不要超过N/5。例如25个月的数据，样本外最多预测到25/5=5年的数据。所以预测9个月的数据，最少最少要45个月的样本。除非你有足够的数据支撑你的预测数据，否则不适合做长时间的预测。

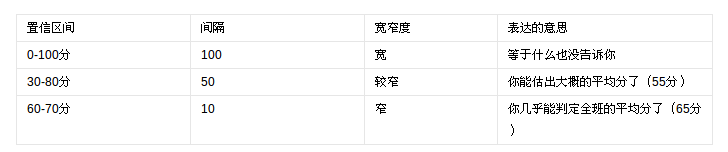
6、置信区间
较窄的置信区间比较宽的置信区间能提供更多的有关总体参数的信息 [1] 。举例说明如下：
假设全班考试的平均分数为65分，则有如下表格中的理解：

7、dropna()

详解：https://blog.csdn.net/weixin_38168620/article/details/79596798

滤除缺失数据，可通过设置参数滤除包含NAN值的行，或者所有字段都为NAN值的行.默认滤除所有包含NaN的行

8、ACF：自相关系数 PACF：偏自相关函数

相关系数度量指的是两个不同事件彼此之间的相互影响程度；而自相关系数度量的是同一事件在两个不同时期之间的相关程度，形象的讲就是度量自己过去的行为对自己现在的影响。
计量经济与时间序列_时间序列分析的几个基本概念(自相关函数,偏自相关函数等)：https://www.cnblogs.com/noah0532/p/8449638.html
代码及解析：https://www.cnblogs.com/bradleon/p/6832867.html

9、衡量机器学习模型的三大指标：准确率、精度和召回率
https://www.cnblogs.com/xuexuefirst/p/8858274.html

10、Pandas中loc和iloc函数

11、pandas的to_csv()使用方法

to_csv()是DataFrame类的方法，read_csv()是pandas的方法

import os

os.getcwd() #获取当前工作路径 

dt.to_csv('Result.csv') #相对位置，保存在getwcd()获得的路径下，dt是Dataframe的一个实例
dt.to_csv('C:/Users/think/Desktop/Result.csv')    #绝对位置

12、datetime
datetime是Python处理日期和时间的标准库。

datetime是模块，datetime模块还包含一个datetime类，通过from datetime import datetime导入的才是datetime这个类。如果仅导入import datetime，则必须引用全名datetime.datetime。datetime.now()返回当前日期和时间，其类型是datetime。
原文：Python学习笔记——datatime和pandas.to_datetime：https://blog.csdn.net/qq_32607273/article/details/81809986

13、BIC值
表示模型对数据的释度，BIC值越小，该模型对数据解释力越强，你可以理解成BIC越小越好，如果值为负，是要带上负号比较的。

hon] 时间序列分析之ARIMA：https://blog.csdn.net/u010414589/article/details/49622625

AR(I)MA时间序列建模过程——步骤和python代码：https://www.jianshu.com/p/cced6617b423

14、pandas相关操作

astype()函数

astype()函数可用于转化dateframe某一列的数据类型

15、对列、行求最大、最小值

pandas的数据结构常用到一维(series)，二维(DataFrame)等：
对于二维数据，二维数据包含行索引和列索引
行索引叫index，axis=0　　列索引叫columns，axis=1
#对列求最大值
test_data_frame.max(0)　　
对行求最大值　　
test_data_frame.max(1)　　
求最小值同理　　
test_data_frame.max(0)
对列求最小值　　
test_data_frame.max(1)
对行求最小值

获取最大值和最小值的位置　　
获取列最大值的位置　　
test_data_frame.idxmax(axis=0)　　# 获取行最大值的位置　　test_data_frame.idxmax(axis=1)　　# 获取列最小值得位置　　test_data_frame.idxmin(axis=0)　　# 获取行最小值得位置，默认是0　　test_data_frame.idxmin(axis=1)

累计求和

# 累计求第二列的值　
test_data_frame.column1.cumsum()　
不能使用test_data_frame.row1.cumsum()累计求行的和

参考：https://blog.51cto.com/14335413/2428815

ARIMA模型原理及实现：https://www.jianshu.com/p/305c4961ee06