卷积神经网络

卷积神经网络

卷积神经⽹络(convolutional neural network)是含有卷积层(convolutional layer)的神经⽹络，主要包含：卷积层、池化层。

卷积层(Convolution：Conv)

卷积运算

虽然卷积层得名于卷积(convolution)运算，但在卷积层中使用的互相(crosscorrelation)运算。使用卷积核 (kernel, filter) ，从输⼊数组的最左上⽅开始，按从左往右、从上往下的顺序，依次在输⼊数组上滑动，不断地和其大小相同的部分做对应元素的 乘法 并 求和，得到的数字作为输出的元素值。卷积运算的符号用 ∗ 符号表示。

如果，图片的维度为 $n\times n$ ，卷积核 (kernel) 的维度为 $f\times f$ ，卷积后维度为：$(n-f+1)\times (n-f+1)$ 。

通道数 (channel)

立体卷积

对于彩色图像中，因为图片有R、G、B三个颜色通道，此时的卷积核为三维卷积核。卷积核的第三个维度需要与进行卷积运算的图片的通道数相同。三维卷积核的运算一样是与其维度相同的部分做对应元素间的乘法并求和，最终得到一个二维的结果。

多卷积核

单个卷积核应用于图片时，提取图片特定的特征，不同的卷积核提取不同的特征。

如果，图片的维度为 $n_c\times n\times n$，卷积核 (filter) 的维度为 $n_c^{\prime }\times n_c\times f\times f$ ，卷积后维度为：$n_c^{\prime }\times (n-f+1)\times (n-f+1)$ 。其中： $n_c$ 表示图片的通道数， $n_c^{\prime }$ 表示为卷积核的个数，也是输出的通道数。

Padding

没有 Padding 的缺点：每次卷积操作，图片会缩小：$(n-f+1)\times (n-f+1)$ 。角落和边缘位置的像素进行卷积运算的次数少，可能会丢失有用信息。

填充(Padding)是指在输⼊矩阵周围填充元素(通常是 $0$ 元素)。以 $p$ 表示 Padding 的维度，则卷积输出维度为： $(n+2p-f+1)\times (n+2p-f+1)$ 。

Same padding，输出与输入图片大小相同，$p=(f-1)/2$ 。如果是偶数，此时padding上下左右维度不相等。卷积神经⽹络经常使⽤奇数⾼宽的卷积核，如1、3、5和7，所以两端上的填充维度相等。

卷积步长(stride)

每次的卷积核移动的步长 (stride)。以s表示stride的大小，则卷积输出维度为：
$$\lfloor \frac{n+2p-f}{s}+1\rfloor \times \lfloor \frac{n+2p-f}{s}+1\rfloor$$
PyTroch 实现：torch.nn.Conv2d

1x1卷积

使用 $n_c^{\prime }\times n_c\times 1\times 1$ 卷积核进行卷积，相当于图像的 $n_c^{\prime }$ 个 $n_c\times 1\times 1$ 切片乘以卷积数值权重。实际上，$1\times 1$ 卷积的主要计算发⽣在通道维上，输出中的每个元素来⾃输⼊中在⾼和宽上相同位置的元素在不同通道之间的按权重累加。相当于对多个通道上的单元应用了一个全连接的神经网络。最终三维的图形应用 $1\times 1$ 的卷积核得到一个相同长宽但第三维度变为卷积核个数的图片。

通常 $1\times 1$ 卷积用于调整网络层之间的通道数，并控制模型的复杂度：

• 维度压缩：使用目标维度的1×1的卷积核个数。
• 增加非线性：保持与原维度相同的1×1的卷积核个数。

pytorch 实现：torch.nn.Conv1d

池化层(Pooling：Pool)

我们感兴趣的物体不会总出现在固定位置，进而对后⾯的模式识别造成不便。使用池化层可以缓解卷积层对位置的过度敏感性。与卷基层一样，池化层也有使用池化核在输入矩阵上滑动，不同 的是在处理多通道输⼊数据时，池化层对每个输⼊通道分别池化，而不是像卷积层那样将各通道的输⼊按通道相加。需要注意的是池化层没有需要学习的参数。

池化层分为两类：

• 最大池化(Max Pooling)：最大池化是仅由当前小区域内的最大值来代表最终池化后的值。
• 平均池化(Average Pooling)：平均池化是其选取的是小区域内的均值来代表该区域内的值。

池化后输出维度为：
$$\lfloor \frac{n+2p-f}{s}+1\rfloor \times \lfloor \frac{n+2p-f}{s}+1\rfloor$$

pytorch 实现：torch.nn.MaxPool2d torch.nn.AvgPool2d

卷积神经网络的优点

1. 降低计算量；
2. 参数共享：一个特征检测器(filter)对图片的一部分有用的同时也有可能对图片的另外一部分有用；
3. 连接的稀疏性：在每一层中，每个输出值只取决于少量的输入。

经典模型

介绍几种经典的卷积神经网络结构，分别是LeNet、AlexNet、VGGNet、ResNet 和 Inception Network。

LeNet-5

LeNet分为卷积层块和全连接层块两个部分，具体结构如下：

Conv——Pool——Conv——Pool——Fc——Fc——Fc——softmax。

卷积层块⾥的基本单位是卷积层后接最⼤池化层：卷积层⽤来识别图像⾥的空间模式，如线条和
物体局部，之后的最⼤池化层则⽤来降低卷积层对位置的敏感性。卷积层块由两个这样的基本单
位重复堆叠构成。在卷积层块中，每个卷积层都使⽤ $5\times 5$ 的窗口，并在输出上使⽤ sigmoid 激活函数。第⼀个卷积层输出通道数为 $6$，第⼆个卷积层输出通道数则增加到 $16$。这是因为第⼆个卷积层⽐第⼀个卷积层的输⼊的⾼和宽要小，所以增加输出通道使两个卷积层的参数尺⼨类似。卷积层块的两个最⼤池化层的窗口形状均为 $2\times 2$，且步幅为 $2$。由于池化窗口与步幅形状相同，池化窗口在输⼊上每次滑动所覆盖的区域互不重叠。
卷积层块的输出形状为 [batch_size, channel, height, weight]。当卷积层块的输出传⼊全连接层块时，全连接层块会将小批量中每个样本变平(flatten)。也就是说，全连接层的输⼊形状将变成⼆维 [batch_size, channel * height * weight]。全连接层块含3个全连接层。它们的输出个数分别是120、84和10，其中10为输出的类别个数。

LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278-2324.

AlexNet

AlexNet 的结构与 LeNet-5 相似，相对于LeNet-5的改进如下：

1. 增加网络层数。与相对较小的LeNet相⽐，AlexNet包含8层变换，其中有5层卷积和2层全连接隐藏层，以及1个全连接输出层。AlexNet第⼀层中的卷积窗口为 $11\times 11$。第⼆层中的卷积窗口为 $5\times 5$，之后的卷积窗口都全采⽤ $3\times 3$ 大小。此外，第⼀、第⼆和第五个卷积层之后都使⽤了窗口形状为 $3\times 3$ 、步幅为 $2$ 的最⼤池化层。紧接着最后⼀个卷积层的是两个输出个数为 $4096$ 的全连接层。
2. 使用 ReLU 激活函数。AlexNet将sigmoid激活函数改成了更加简单的ReLU激活函数。⼀⽅⾯，ReLU激活函数的计算更简单，例如它并没有sigmoid激活函数中的求幂运算。另⼀⽅⾯，ReLU激活函数在不同的参数初始化⽅法下使模型更容易训练。这是由于当sigmoid激活函数输出极接近0或1时，这些区域的梯度⼏乎为0，从而造成反向传播⽆法继续更新部分模型参数；而ReLU激活函数在正区间的梯度恒为1。因此，若模型参数初始化不当，sigmoid函数可能在正区间得到⼏乎为0的梯度，从而令模型⽆法得到有效训练。
3. 使用 dropout。AlexNet通过丢弃法(参⻅“丢弃法”⼀节)来控制全连接层的模型复杂度。而LeNet并没有使⽤丢弃法。
4. AlexNet引⼊了⼤量的图像增⼴，如翻转、裁剪和颜⾊变化，从而进⼀步扩⼤数据集来缓解过拟合。

Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). Imagenet classification with deep convolutionalneural networks. In Advances in neural information processing systems (pp. 1097-1105).

VGG- 16

VGG提出了可以通过重复使⽤简单的 基础块 来构建深度模型的思路。

VGG块的组成规律是：连续使⽤数个 相同 的填充为 $1$、窗口形状为 $3\times 3$ 的卷积层。每一个卷积快最后接上⼀个步幅为 $2$、窗口形状为 $2\times 2$ 的最⼤池化层。卷积层保持输⼊的⾼和宽不变，而池化层则对其减半。它有 $5$ 个卷积块，前 $2$ 块使⽤双卷积层，而后 $3$ 块使⽤三卷积层。第⼀块的输出通道是 $64$，之后每次对输出通道数翻倍，直到变为 $512$。因为这个⽹络使⽤了 $13$ 个卷积层和 $3$ 个全连接层，所以经常被称为 VGG-16。

Simonyan, K., & Zisserman, A. (2014). Very deep convolutional networks for large-scaleimage recognition. arXiv preprint arXiv:1409.1556.

ResNet

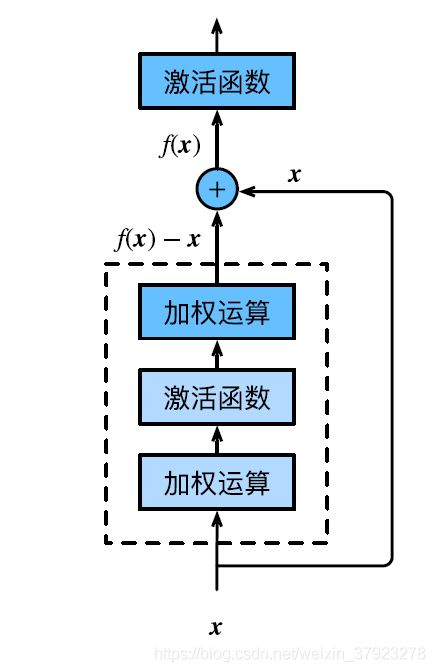
ResNet是由 残差块 所构建。

残差块(residual block)：则将其传播过程增加了一个从 $$a^{[}l]$$ 直接到 $$z^{[}l+2]$$ 的连接，将其称之为 short cut 或者 skip connection，也就是前向传播公式的最后一个步骤变为：
$$a^{[l+2]}=g(z^{[l+2]}+a^{[l]})$$
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yt9iLm8y-1570604313411)(D:\note\markdown\深度学习\assets\1570548137070.png)]

残差块的优点？在残差块中，输⼊可通过跨层的数据线路更快地向前传播。ResNet对于中间的激活函数来说，有助于能够达到更深的网络，解决梯度消失和梯度爆炸的问题。*

[1] He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recognition. In
Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).
[2] He, K., Zhang, X., Ren, S., & Sun, J. (2016, October). Identity mappings in deep residual
networks. In European Conference on Computer Vision (pp. 630-645). Springer, Cham.

Inception Network

基础卷积块叫作Inception块，得名于电影《盗梦空间》(Inception)。

Inception块⾥有4条并⾏的线路。前3条线路使⽤窗口⼤小分别是 $1\times 1$、 $3\times 3$ 和 $5\times 5$ 的卷积层来抽取不同空间尺⼨下的信息，其中中间2个线路会对输⼊先做 $1\times 1$ 卷积来减少输⼊通道数，以降低模型复杂度。第四条线路则使⽤ $3\times 3$ 最⼤池化层，后接 $1\times 1$ 卷积层来改变通道数。4条线路都使⽤了合适的填充来使输⼊与输出的⾼和宽⼀致。最后我们将每条线路的输
出在通道维上连结，并输⼊接下来的层中去。

为什么好？

[1] Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., & Anguelov, D. & Rabinovich, A.(2015).
Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision
and pattern recognition (pp. 1-9).
[2] Ioffe, S., & Szegedy, C. (2015). Batch normalization: Accelerating deep network training by
reducing internal covariate shift. arXiv preprint arXiv:1502.03167.
[3] Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., & Wojna, Z. (2016). Rethinking the inception
architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision
and Pattern Recognition (pp. 2818-2826).
[4] Szegedy, C., Ioffe, S., Vanhoucke, V., & Alemi, A. A. (2017, February). Inception-v4,
inception-resnet and the impact of residual connections on learning. In Proceedings of the
AAAI Conference on Artificial Intelligence (Vol. 4, p. 12).

附录

数学中的卷积与互关系

在数学定义上，矩阵的卷积(convolution)操作为首先将卷积核180°进行旋转，构成一个卷积核的镜像，然后使用该镜像再和前面的矩阵进行移动相乘求和操作。在深度学习中，我们所谓的卷积运算实则没有卷积核变换为镜像的这一步操作，因为权重 (weight) 学习是学习得到的，所以变换是没有必要的。深度学习的卷积操作在数学上准确度来说称为互相关(cross-correlation)。

卷积层为何能使⽤互相关运算替代卷积运算。其实，在深度学习中核数组都是学出来的：卷积层⽆论使⽤互相关运算或卷积运算都不影响模型预测时的输出。

卷积与边缘检测

边缘检测通过垂直、水平边缘 filter 可以明显地将边缘和非边缘区分出来。所以，卷积运算能够检测图像中的边缘，成为卷积神经网络中重要的一部分。如果，将filter中的数字直接看作是需要学习的参数，其可以学习到更复杂的filter，也许可以知道不同角度的边缘。输出其提取到的所有有用的特征。

参考

• 吴恩达卷积神经网络
• 动手深度学习 PyTorch 代码
• 万字长文带你看尽深度学习中的各种卷积网络 英文原文