【计算机视觉】图像分类

前言

       在当前的网络时代及信息时代，越来越多图像问题需要解决，当然计算机就起到很重要的作用。图像分类和图像内容分类算法就可以采用一些简单有效的方法和目前一些性能最好的分类器，解决两类和多类问题。在图像分类中，最简单且最常用的一种方法就是KNN（邻近分类法），用于手势识别和目标识别具有很大成就。

目录

（一）K邻近分类法

（1）实现二维的可视化KNN

（2）dense sift原理

（3）实现手势识别

（4）遇到的问题

（二）代码下载

---

---

（一）K邻近分类法

     KNN算法就是把要分类的对象（例如一个特征向量）与训练集中已知类标记的所有对象进行对比，并由K近邻对分类对象进行判断为那个类别。这种方法的效果好，但是也有弊端：与K-means聚类算法一样，需要先预定设置K的值，k值的选择会影响分类的性能；此外这种方法要求整个训练集存储起来，如果训练集越大，搜索就越慢，训练集越小，分类结果准确率也越低。对于大的训练集，采取某些装箱形式通常会减少对比的次数，从积极一面看，这种采用何种距离度量方面是没有限制的；实际上对于想达到的结果起到一定的作用，但是并不代表这种算法分类性能很高，它的可行性一般。

（1）实现二维的可视化KNN

步骤1.创建二维示例数据集的代码如下：

# -*- coding: utf-8 -*-
from numpy.random import randn
import pickle
from pylab import *

# create sample data of 2D points
n = 200
# two normal distributions
class_1 = 0.6 * randn(n,2)
class_2 = 1.2 * randn(n,2) + array([5,1])
labels = hstack((ones(n),-ones(n)))
# save with Pickle
#with open('points_normal.pkl', 'w') as f:
with open('points_normal_test.pkl', 'wb') as f:
    pickle.dump(class_1,f)
    pickle.dump(class_2,f)
    pickle.dump(labels,f)
# normal distribution and ring around it
print ("save OK!")
class_1 = 0.6 * randn(n,2)
r = 0.8 * randn(n,1) + 5
angle = 2*pi * randn(n,1)
class_2 = hstack((r*cos(angle),r*sin(angle)))
labels = hstack((ones(n),-ones(n)))
# save with Pickle
#with open('points_ring.pkl', 'w') as f:
with open('points_ring_test.pkl', 'wb') as f:
    pickle.dump(class_1,f)
    pickle.dump(class_2,f)
    pickle.dump(labels,f)
    
print ("save OK!")

   上面的脚本代码将创建两个不同的二维点集，每个点有两类，用Pickle模块保存创建的数据；要注意的是：要用不同的文件名运行脚本两次，例如第一次用代码中的文件名进行保存，第二次将代码中的points_normal_t.pkl和points_ring_pkl分别改为points_normal_test.pkl和points_ring_test.pkl进行保存。这是因为可以得到4个不同的二维的数据集文件，可以讲一个用来训练，另一个用来做测试。

步骤2.用knn算法进行分类

# -*- coding: utf-8 -*-
import pickle
from pylab import *
from PCV.classifiers import knn
from PCV.tools import imtools

pklist=['points_normal.pkl','points_ring.pkl']

figure()

# load 2D points using Pickle
for i, pklfile in enumerate(pklist):
    with open(pklfile, 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)
    # load test data using Pickle
    with open(pklfile[:-4]+'_test.pkl', 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)

    model = knn.KnnClassifier(labels,vstack((class_1,class_2)))#构造分类器
    # test on the first point
    print (model.classify(class_1[0]))

    #define function for plotting
    def classify(x,y,model=model):
        return array([model.classify([xx,yy]) for (xx,yy) in zip(x,y)])

    # lot the classification boundary
    subplot(1,2,i+1)
    imtools.plot_2D_boundary([-6,6,-6,6],[class_1,class_2],classify,[1,-1])
    titlename=pklfile[:-4]
    title(titlename)
#savefig("test.png")
show()

脚本里用到Pickle模块创建一个KNN分类器模型。为了可视化所有测试数据点的分类，并展示分类器分类效果如何，创建了一个辅助函数以获取x和y二维坐标数组和分类器，并返回一个预测的类标记数组，然后把函数作为参数传递给实际的绘制函数。其中能够做出分类线的是plot_2D_boundary(plot_range,points,decisionfcn,labels,values=[0])  （plot_range为（xmin,xmax,ymin,ymax），points是类数据点列表，decisionfcn是评估函数，labels,是函数decisionfcn关于每个类返回的标记列表）；这个函数需要一个决策函数（分类器），并用meshgrid（）函数在一个网格上进行预测。决策函数的等值线可以显示边界位置，默认边界为零等值线。画出的结果如下图所示：

（2）dense sift原理

     dense SIFT在目标分类和场景分类有重要的应用。dense SIFT经常会用在bag of words 模型中。如以16×16 pixel大小的size和8 pixels的stepsize提取dense SIFT特征，然后做max pooling……。引出dense SIFT与做特征匹配所用到的SIFT的不同点。dense SIFT是提取我们感兴趣的patches中的每个位置的SIFT特征。而通常做特征匹配的SIFT算法只是得到感兴趣区域或者图像上若干个稳定的关键点的SIFT特征。

     如图所示，目前关于dense SIFT提取比较流行的做法是，拿一个size固定的掩模或者bounding box，以一定的步长（stepsize）在图像上自左向右、从上到下提取dense SIFT的patch块。

dsift与sift的区别在于：

Dense SIFT:不构建高斯尺度空间，只在a single scale上提取SIFT特征，可以得到每一个位置的SIFT descriptor；

SIFT:需要构建高斯尺度空间，只能得到Lowe算法计算得到的点的SIFT descriptor；

（3）实现手势识别

在图像分类范围中，手势识别一般会用到稠密sift描述算子来表示这些手势图像。首先对手势图像数据集（训练集、测试集）的每张图像都进行创建.dsift文件，用于保存读取到的图像特征，再进行创建标记，以便于进行手势识别。然后对这些数据使用KNN算法进行分类。在通过所得到的dsift文件读取手势图像的稠密sift描述算子及标记。

生成稠密描述算子代码如下：

# -*- coding: utf-8 -*-
#from PCV.localdescriptors import dsift
import dsift
import os
#from PCV.localdescriptors import sift
import sift
from pylab import *
from PCV.classifiers import knn

def get_imagelist(path):
    """    Returns a list of filenames for
        all jpg images in a directory. """

    return [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.jpg')]

def read_gesture_features_labels(path):
    # create list of all files ending in .dsift
    featlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.dsift')]
    # read the features
    features = []
    for featfile in featlist:
        l,d = sift.read_features_from_file(featfile)
        features.append(d.flatten())
    features = array(features)
    # create labels
    labels = [featfile.split('/')[-1][0] for featfile in featlist]
    return features,array(labels)

def print_confusion(res,labels,classnames):
    n = len(classnames)
    # confusion matrix
    class_ind = dict([(classnames[i],i) for i in range(n)])
    confuse = zeros((n,n))
    for i in range(len(test_labels)):
        confuse[class_ind[res[i]],class_ind[test_labels[i]]] += 1
    print ('Confusion matrix for')
    print (classnames)
    print (confuse)

filelist_train = get_imagelist('gesture1/train')
filelist_test = get_imagelist('gesture1/test')
imlist=filelist_train+filelist_test

# process images at fixed size (50,50)
for filename in imlist:
    featfile = filename[:-3]+'dsift'
    dsift.process_image_dsift(filename,featfile,10,5,resize=(50,50))
#读取训练集
features,labels = read_gesture_features_labels('gesture1/train/')
test_features,test_labels = read_gesture_features_labels('gesture1/test/')
classnames = unique(labels)

# test kNN
k = 1
knn_classifier = knn.KnnClassifier(labels,features)
res = array([knn_classifier.classify(test_features[i],k) for i in
range(len(test_labels))])
# accuracy准确率
acc = sum(1.0*(res==test_labels)) / len(test_labels)
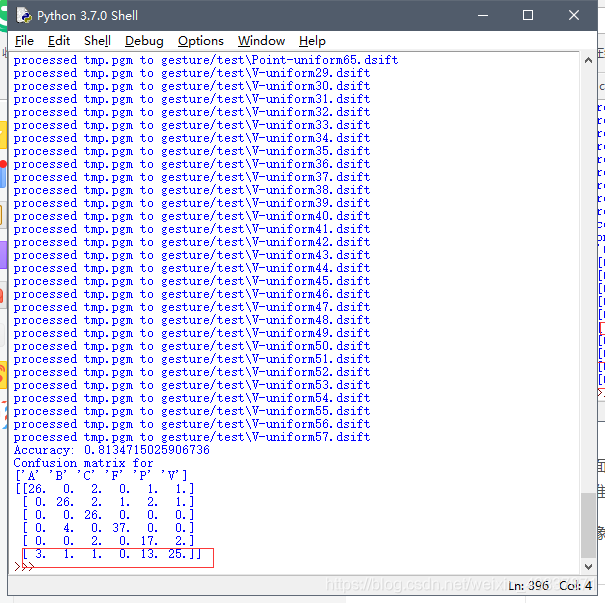
print ('Accuracy:', acc)

print_confusion(res,test_labels,classnames)

上面代码不仅得到每张图像的dsift文件也计算出在训练和测试对手势图像进行knn算法测试分类的准确率结果。

图像集（对gesture1图像文件）较少的情况：

上面的正确率比较低，这是因为手势图像训练集和测试集小的原因，测试不够会影响分类器的测试性能，图像集越小，训练度不够准确率就很低。

图像集（对gesture图像文件）较多的情况：

不管是图像集大还是较小，虽然上面的正确率显示了对于给定的测试集有多少图像是正确分类的，但是他并没有告诉哪些手势是难以分类。为此，混淆矩阵是一个可以显示每个类有多少的个样本被分在每一类中的矩阵，它可以显示错误的分布情况以及哪些是经常错误混淆的图像。对于图像训练集较少的情况会出现较多的混淆情况（由上面红色线框标记出5和0/6/7，9和1会出现分类混淆），在图像训练集较多的情况虽然混淆情况较少但是也会出现相似的特征的分类混淆错误（P和V出现分类混淆）。会出现分类混淆是因为不管是sift算法还是稠密sift算法提取图像特征都会出现相似点对的错误匹配，对于图像分类来说还有的错误混淆的原因还有，对于图像相似，特征点也会相似，所以手势相近的图像分类是会出现分类混淆。

绘制带有描述算子的手势图像代码实现如下：

# -*- coding: utf-8 -*-
import os
import sift, dsift
from pylab import  *
from PIL import Image
'''
imlist=['gesture1/train/0-train00.jpg','gesture1/train/1-train01.jpg',
        'gesture1/train/2-train02.jpg','gesture1/train/3-train03.jpg',
        'gesture1/train/4-train04.jpg','gesture1/train/5-train05.jpg',
        'gesture1/train/6-train06.jpg','gesture1/train/7-train07.jpg',
        'gesture1/train/8-train08.jpg','gesture1/train/9-train09.jpg',
        'gesture1/train/520-train520.jpg']'''

imlist=['gesture1/train/0-train00.jpg','gesture1/train/1-train01.jpg',
        'gesture1/train/2-train02.jpg','gesture1/train/3-train03.jpg',
        'gesture1/train/4-train04.jpg','gesture1/train/5-train05.jpg',
        'gesture1/train/6-train06.jpg','gesture1/train/7-train07.jpg',
        'gesture1/train/8-train08.jpg']

figure()
for i, im in enumerate(imlist):
    print (im)
    dsift.process_image_dsift(im,im[:-3]+'dsift',90,40,True)
    l,d = sift.read_features_from_file(im[:-3]+'dsift')
    dirpath, filename=os.path.split(im)
    im = array(Image.open(im))
    #显示手势含义title
    titlename=filename[:-12]
    #titlename=filename[:-14]
    subplot(3,3,i+1)
    sift.plot_features(im,l,True)
    title(titlename)
show()

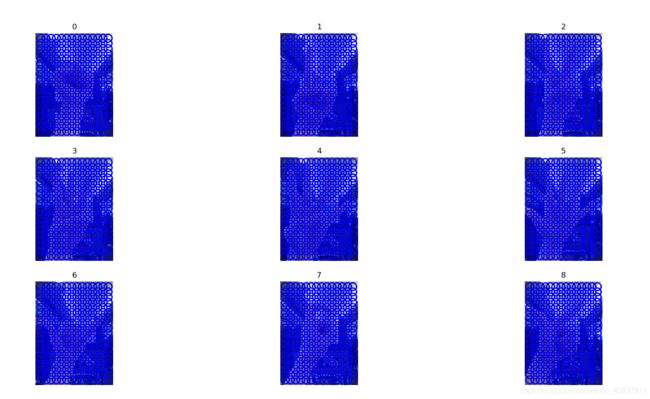
上面代码比较好理解，就是对要识别的手势图像存入列表imlist里，再进行读取相对应的稠密sift描述算子，最后显示出对应图像信息。注意：这里将图像分表率调成固定大小且不要太大。这很重要，否则这些图像会有不同数量的描述算子，从而描述算子的特征向量长度也不一样，会导致在后面比较时出错。

gesture图像集的相关图像显示：

gesture1图像集的相关图像显示：

（4）遇到的问题

1.出现这样的错误，表示你的图像集有9个分类，但是训练的时候没有第九个分类情况，只要加入一个分类情况即可。

2.出现找不到.dsift文件情况，这一般是PCV包sift或者dsift文件的错误，把读取sift.exe的路径改一下即可。例如：sift文件的路径读取情况：

因为我配置sift.exe环境时放在当前项目里

具体sift环境配置，查看链接：https://blog.csdn.net/weixin_43837871/article/details/88604483

dsift修改同上操作。

（二）代码下载

链接：代码下载 
提取码：bbgo