在HT for Web中2D和3D应用都支持树状结构数据的展示,展现效果各异,2D上的树状结构在展现层级关系明显,但是如果数据量大的话,看起来就没那么直观,找到指定的节点比较困难,而3D上的树状结构在展现上配合HT for Web的弹力布局组件会显得比较直观,一眼望去可以把整个树状结构数据看个大概,但是在弹力布局的作用下,其层次结构看得就不是那么清晰了。所以这时候结构清晰的3D树的需求就来了,那么这个3D树具体长成啥样呢,我们来一起目睹下~
要实现这样的效果,该从何下手呢?接下来我们就将这个问题拆解成若干个小问题来解决。
1.创建一个树状结构
有了解过HT for Web的朋友,对树状结构数据的创建应该都不陌生,在这里我就不做深入的探讨了。树状结构数据的创建很简单,在这里为了让代码更简洁,我封装了三个方法来创建树状结构数据,具体代码如下:
/**
* 创建连线
* @param {ht.DataModel} dataModel - 数据容器
* @param {ht.Node} source - 起点
* @param {ht.Node} target - 终点
*/
function createEdge(dataModel, source, target) {
// 创建连线,链接父亲节点及孩子节点
var edge = new ht.Edge();
edge.setSource(source);
edge.setTarget(target);
dataModel.add(edge);
}
/**
* 创建节点对象
* @param {ht.DataModel} dataModel - 数据容器
* @param {ht.Node} [parent] - 父亲节点
* @returns {ht.Node} 节点对象
*/
function createNode(dataModel, parent) {
var node = new ht.Node();
if (parent) {
// 设置父亲节点
node.setParent(parent);
createEdge(dataModel, parent, node);
}
// 添加到数据容器中
dataModel.add(node);
return node;
}
/**
* 创建结构树
* @param {ht.DataModel} dataModel - 数据容器
* @param {ht.Node} parent - 父亲节点
* @param {Number} level - 深度
* @param {Array} count - 每层节点个数
* @param {function(ht.Node, Number, Number)} callback - 回调函数(节点对象,节点对应的层级,节点在层级中的编号)
*/
function createTreeNodes(dataModel, parent, level, count, callback) {
level--;
var num = (typeof count === 'number' ? count : count[level]);
while (num--) {
var node = createNode(dataModel, parent);
// 调用回调函数,用户可以在回调里面设置节点相关属性
callback(node, level, num);
if (level === 0) continue;
// 递归调用创建孩子节点
createTreeNodes(dataModel, node, level, count, callback);
}
}嘿嘿,代码写得可能有些复杂了,简单的做法就是嵌套几个for循环来创建树状结构数据,在这里我就不多说了,接下来我们来探究第二个问题。
2.在2D拓扑下模拟3D树状结构每层的半径计算
在3D下的树状结构体最大的问题就在于,每个节点的层次及每层节点围绕其父亲节点的半径计算。现在树状结构数据已经有了,那么接下来就该开始计算半径了,我们从两层树状结构开始推算:
我现在先创建了两层的树状结构,所有的子节点是一字排开,并没有环绕其父亲节点,那么我们该如何去确定这些孩子节点的位置呢?
首先我们得知道,每个末端节点都有一圈属于自己的领域,不然节点与节点之间将会存在重叠的情况,所以在这里,我们假定末端节点的领域半径为25,那么两个相邻节点之间的最短距离将是两倍的节点领域半径,也就是50,而这些末端节点将均匀地围绕在其父亲节点四周,那么相邻两个节点的张角就可以确认出来,有了张角,有了两点间的距离,那么节点绕其父亲节点的最短半径也就能计算出来了,假设张角为a,两点间最小距离为b,那么最小半径r的计算公式为:
r = b / 2 / sin(a / 2);
那么接下来我么就来布局下这个树,代码是这样写的:
/**
* 布局树
* @param {ht.Node} root - 根节点
* @param {Number} [minR] - 末端节点的最小半径
*/
function layout(root, minR) {
// 设置默认半径
minR = (minR == null ? 25 : minR);
// 获取到所有的孩子节点对象数组
var children = root.getChildren().toArray();
// 获取孩子节点个数
var len = children.length;
// 计算张角
var degree = Math.PI * 2 / len;
// 根据三角函数计算绕父亲节点的半径
var sin = Math.sin(degree / 2),
r = minR / sin;
// 获取父亲节点的位置坐标
var rootPosition = root.p();
children.forEach(function(child, index) {
// 根据三角函数计算每个节点相对于父亲节点的偏移量
var s = Math.sin(degree * index),
c = Math.cos(degree * index),
x = s * r,
y = c * r;
// 设置孩子节点的位置坐标
child.p(x + rootPosition.x, y + rootPosition.y);
});
}
在代码中,你会发现我将末端半径默认设置为25了,如此,我们通过调用layout()方法就可以对结构树进行布局了,其布局效果如下: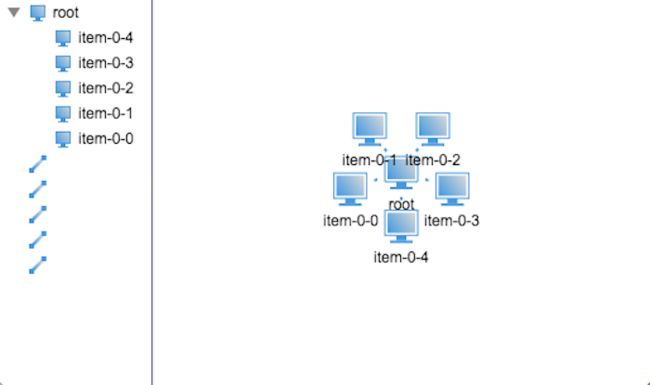
不行,节点都重叠在一起了,看来简单的递归是不行的,那么具体的问题出在哪里呢?
仔细分析了下,发现父亲节点的领域半径是由其孩子节点的领域半径决定的,因此在布局时需要知道自身节点的领域半径,而且节点的位置取决于父亲节点的领域半径及位置信息,这样一来就无法边计算半径边布局节点位置了。
那么现在只能将半径的计算和布局分开来,做两步操作了,我们先来分析下节点半径的计算:
首先需要明确最关键的条件,父亲节点的半径取决于其孩子节点的半径,这个条件告诉我们,只能从下往上计算节点半径,因此我们设计的递归函数必须是先递归后计算,废话不多说,我们来看下具体的代码实现:
/**
* 就按节点领域半径
* @param {ht.Node} root - 根节点对象
* @param {Number} minR - 最小半径
*/
function countRadius(root, minR) {
minR = (minR == null ? 25 : minR);
// 若果是末端节点,则设置其半径为最小半径
if (!root.hasChildren()) {
root.a('radius', minR);
return;
}
// 遍历孩子节点递归计算半径
var children = root.getChildren();
children.each(function(child) {
countRadius(child, minR);
});
var child0 = root.getChildAt(0);
// 获取孩子节点半径
var radius = child0.a('radius');
// 计算子节点的1/2张角
var degree = Math.PI / children.size();
// 计算父亲节点的半径
var pRadius = radius / Math.sin(degree);
// 设置父亲节点的半径及其孩子节点的布局张角
root.a('radius', pRadius);
root.a('degree', degree * 2);
}OK,半径的计算解决了,那么接下来就该解决布局问题了,布局树状结构数据需要明确:孩子节点的坐标位置取决于其父亲节点的坐标位置,因此布局的递归方式和计算半径的递归方式不同,我们需要先布局父亲节点再递归布局孩子节点,具体看看代码吧:
/**
* 布局树
* @param {ht.Node} root - 根节点
*/
function layout(root) {
// 获取到所有的孩子节点对象数组
var children = root.getChildren().toArray();
// 获取孩子节点个数
var len = children.length;
// 计算张角
var degree = root.a('degree');
// 根据三角函数计算绕父亲节点的半径
var r = root.a('radius');
// 获取父亲节点的位置坐标
var rootPosition = root.p();
children.forEach(function(child, index) {
// 根据三角函数计算每个节点相对于父亲节点的偏移量
var s = Math.sin(degree * index),
c = Math.cos(degree * index),
x = s * r,
y = c * r;
// 设置孩子节点的位置坐标
child.p(x + rootPosition.x, y + rootPosition.y);
// 递归调用布局孩子节点
layout(child);
});
}
代码写完了,接下来就是见证奇迹的时刻了,我们来看看效果图吧: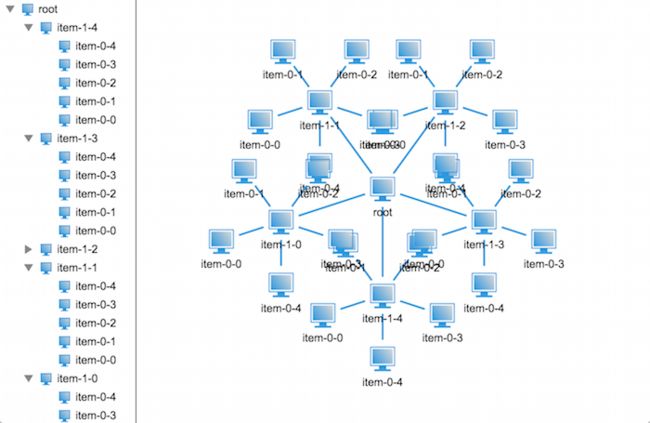
不对呀,代码应该是没问题的呀,为什么显示出来的效果还是会重叠呢?不过仔细观察我们可以发现相比上个版本的布局会好很多,至少这次只是末端节点重叠了,那么问题出在哪里呢?
不知道大家有没有发现,排除节点自身的大小,倒数第二层节点与节点之间的领域是相切的,那么也就是说节点的半径不仅和其孩子节点的半径有关,还与其孙子节点的半径有关,那我们把计算节点半径的方法改造下,将孙子节点的半径也考虑进去再看看效果如何,改造后的代码如下:
/**
* 就按节点领域半径
* @param {ht.Node} root - 根节点对象
* @param {Number} minR - 最小半径
*/
function countRadius(root, minR) {
……
var child0 = root.getChildAt(0);
// 获取孩子节点半径
var radius = child0.a('radius');
var child00 = child0.getChildAt(0);
// 半径加上孙子节点半径,避免节点重叠
if (child00) radius += child00.a('radius');
……
}下面就来看看效果吧~
哦,NO!这不是我想看到的效果,又重叠了,好讨厌。
不要着急,我们再来仔细分析分析下,在前面,我们提到过一个名词——领域半径,什么是领域半径呢?很简单,就是可以容纳下自身及其所有孩子节点的最小半径,那么问题就来了,末端节点的领域半径为我们指定的最小半径,那么倒数第二层的领域半径是多少呢?并不是我们前面计算出来的半径,而应该加上末端节点自身的领域半径,因为它们之间存在着包含关系,子节点的领域必须包含于其父亲节点的领域中,那我们在看看上图,是不是感觉末端节点的领域被侵占了。那么我们前面计算出来的半径代表着什么呢?前面计算出来的半径其实代表着孩子节点的布局半径,在布局的时候是通过该半径来布局的。
OK,那我们来总结下,节点的领域半径是其下每层节点的布局半径之和,而布局半径需要根据其孩子节点个数及其领域半径共同决定。
好了,我们现在知道问题的所在了,那么我们的代码该如何去实现呢?接着往下看:
/**
* 就按节点领域半径及布局半径
* @param {ht.Node} root - 根节点对象
* @param {Number} minR - 最小半径
*/
function countRadius(root, minR) {
minR = (minR == null ? 25 : minR);
// 若果是末端节点,则设置其布局半径及领域半径为最小半径
if (!root.hasChildren()) {
root.a('radius', minR);
root.a('totalRadius', minR);
return;
}
// 遍历孩子节点递归计算半径
var children = root.getChildren();
children.each(function(child) {
countRadius(child, minR);
});
var child0 = root.getChildAt(0);
// 获取孩子节点半径
var radius = child0.a('radius'),
totalRadius = child0.a('totalRadius');
// 计算子节点的1/2张角
var degree = Math.PI / children.size();
// 计算父亲节点的布局半径
var pRadius = totalRadius / Math.sin(degree);
// 缓存父亲节点的布局半径
root.a('radius', pRadius);
// 缓存父亲节点的领域半径
root.a('totalRadius', pRadius + totalRadius);
// 缓存其孩子节点的布局张角
root.a('degree', degree * 2);
}在代码中我们将节点的领域半径缓存起来,从下往上一层一层地叠加上去。接下来我们一起验证其正确性:
搞定,就是这样子了,2D拓扑上面的布局搞定了,那么接下来该出动3D拓扑啦~
3.加入z轴坐标,呈现3D下的树状结构
3D拓扑上面布局无非就是多加了一个坐标系,而且这个坐标系只是控制节点的高度而已,并不会影响到节点之间的重叠,所以接下来我们来改造下我们的程序,让其能够在3D上正常布局。
也不需要太大的改造,我们只需要修改下布局器并且将2D拓扑组件改成3D拓扑组件就可以了。
/**
* 布局树
* @param {ht.Node} root - 根节点
*/
function layout(root) {
// 获取到所有的孩子节点对象数组
var children = root.getChildren().toArray();
// 获取孩子节点个数
var len = children.length;
// 计算张角
var degree = root.a('degree');
// 根据三角函数计算绕父亲节点的半径
var r = root.a('radius');
// 获取父亲节点的位置坐标
var rootPosition = root.p3();
children.forEach(function(child, index) {
// 根据三角函数计算每个节点相对于父亲节点的偏移量
var s = Math.sin(degree * index),
c = Math.cos(degree * index),
x = s * r,
z = c * r;
// 设置孩子节点的位置坐标
child.p3(x + rootPosition[0], rootPosition[1] - 100, z + rootPosition[2]);
// 递归调用布局孩子节点
layout(child);
});
}
上面是改造成3D布局后的布局器代码,你会发现和2D的布局器代码就差一个坐标系的的计算,其他的都一样,看下在3D上布局的效果: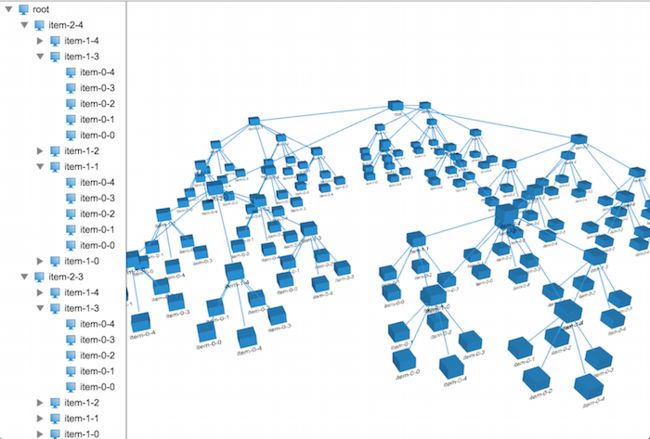
恩,有模有样的了,在文章的开头,我们可以看到每一层的节点都有不同的颜色及大小,这些都是比较简单,在这里我就不做深入的讲解,具体的代码实现如下:
var level = 4,
size = (level + 1) * 20;
var root = createNode(dataModel);
root.setName('root');
root.p(100, 100);
root.s('shape3d', 'sphere');
root.s('shape3d.color', randomColor());
root.s3(size, size, size);
var colors = {},
sizes = {};
createTreeNodes(dataModel, root, level - 1, 5, function(data, level, num) {
if (!colors[level]) {
colors[level] = randomColor();
sizes[level] = (level + 1) * 20;
}
size = sizes[level];
data.setName('item-' + level + '-' + num);
// 设置节点形状为球形
data.s('shape3d', 'sphere');
data.s('shape3d.color', colors[level]);
data.s3(size, size, size);
});在这里引入了一个随机生成颜色值的方法,对每一层随机生成一种颜色,并将节点的形状改成了球形,让页面看起来美观些(其实很丑)。
提个外话,节点上可以贴上图片,还可以设置文字的朝向,可以根据用户的视角动态调整位置,等等一系列的拓展,这些大家都可以去尝试,相信都可以做出一个很漂亮的3D树出来。
到此,整个Demo的制作就结束了,今天的篇幅有些长,感谢大家的耐心阅读,在设计上或则是表达上有什么建议或意见欢迎大家提出,点击这里可以访问HT for Web官网上的手册。