DataWhale基于逻辑回归的分类预测模型

Demo示例

库函数导入

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LogisticRegression

训练模型

#构造数据集
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]])#
y_label = np.array([0, 0, 0, 1, 1, 1])

对应的数据集为

x1	x2	y
-1	-2	0
-2	-1	0
-3	-2	0
1	3	1
2	1	1
3	2	1

#调用逻辑回归模型
lr_clf = LogisticRegression()#实例化LogisticRegression()类
#用逻辑回归模型拟合构造的数据集
lr_clf = lr_clf.fit(x_fearures, y_label) #其拟合方程为 y=w0+w1*x1+w2*x2

模型参数查看

##查看其对应模型的w1和w2 也就是系数
print('the weight of Logistic Regression:',lr_clf.coef_)
##查看其对应模型的w0 也就是截距
print('the intercept(w0) of Logistic Regression:',lr_clf.intercept_)
##the weight of Logistic Regression:[[0.73462087 0.6947908]]
##the intercept(w0) of Logistic Regression:[-0.03643213]
#逻辑回归的拟合结果的.coef_和.intercept_返回的均为list类型，使用时要加以注意

可视化构造的数据样本点

plt.figure()#新建一个画布
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
plt.show()

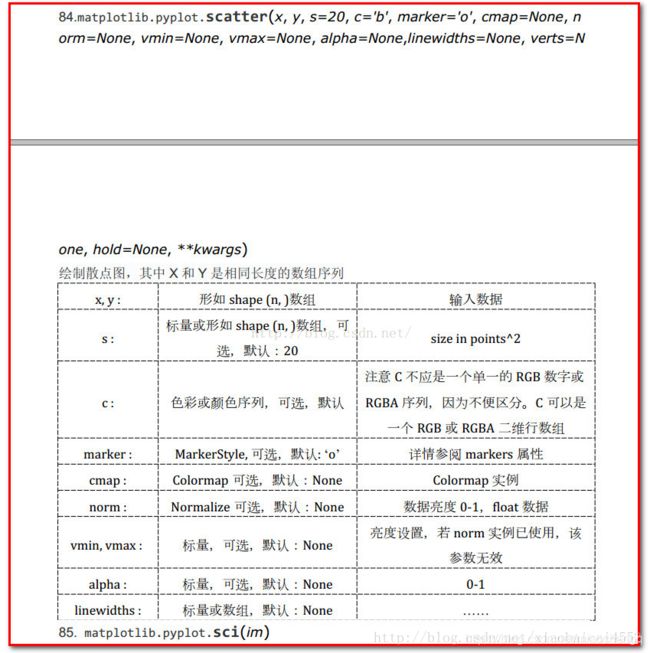
- 其中涉及到matplotlib的使用，请看下图（图片来源于网络）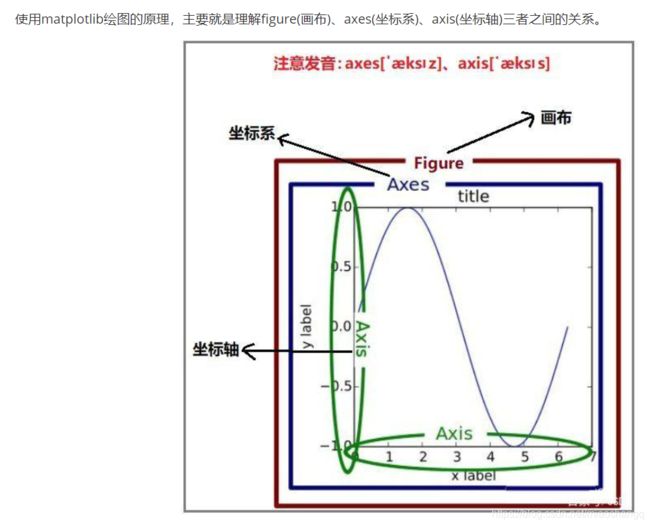
一个figure(画布)上，可以有多个区域axes(坐标系)，我们在每个坐标系上绘图，也就是说每个axes(坐标系)中，都有一个axis(坐标轴)。

- plt.scatter

scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, hold=None, data=None, **kwargs)
#参数说明
'''
    x，y：array_like，shape（n，）
        输入数据
    
    s：标量或array_like，shape（n，），可选
        大小以点数^ 2。默认是`rcParams ['lines.markersize'] ** 2`。
    
    c：颜色，顺序或颜色顺序，可选，默认：'b'
        `c`可以是单个颜色格式的字符串，也可以是一系列颜色
        规范的长度为`N`，或一系列`N`数字
        使用通过kwargs指定的`cmap`和`norm`映射到颜色
        （见下文）。请注意，`c`不应该是单个数字RGB或
        RGBA序列，因为这与数组无法区分
        值将被彩色映射。 `c`可以是一个二维数组，其中的
        行是RGB或RGBA，但是，包括单个的情况
        行为所有点指定相同的颜色。
    
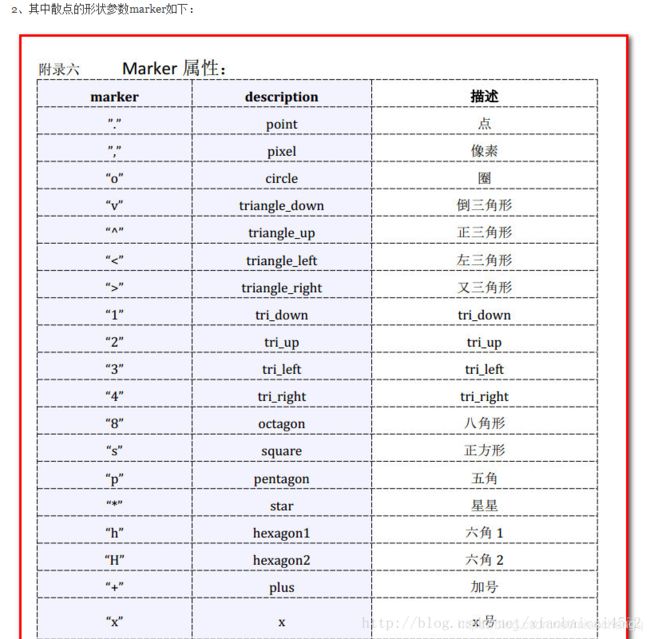
    marker：`〜matplotlib.markers.MarkerStyle`，可选，默认值：'o'
        请参阅`〜matplotlib.markers`以获取有关不同的更多信息
        标记分散支持的样式。 `marker`可以是
        该类的实例或特定文本的简写
        标记。
    
    cmap：`〜matplotlib.colors.Colormap`，可选，默认：无
        一个`〜matplotlib.colors.Colormap`实例或注册名称。
        `cmap`仅在`c`是浮点数组时使用。如果没有，
        默认为rc`image.cmap`。
    
    norm：`〜matplotlib.colors.Normalize`，可选，默认：无
        `〜matplotlib.colors.Normalize`实例用于缩放
        亮度数据为0,1。`norm`只有在`c`是一个数组时才被使用
        彩车。如果`None'，则使用默认值：func：`normalize`。
    
    vmin，vmax：标量，可选，默认值：无
        `vmin`和`vmax`与`norm`结合使用来标准化
        亮度数据。如果其中任何一个都是`无'，那么最小和最大的
        使用颜色数组。请注意，如果你通过一个“规范”实例，你的
        `vmin`和`vmax`的设置将被忽略。
    
    alpha：标量，可选，默认值：无
        alpha混合值，介于0（透明）和1（不透明）之间，
    
    linewidths：标量或array_like，可选，默认值：无
        如果无，则默认为（lines.linewidth，）。
    
    verts：（x，y）的序列，可选
        如果`marker`为None，这些顶点将用于
        构建标记。标记的中心位于
        在（0,0）为标准化单位。整体标记重新调整
        由``s``完成。
    
     edgecolors ：颜色或颜色顺序，可选，默认值：无
        如果无，则默认为'face'
    
        如果'face'，边缘颜色将永远是相同的
        脸色。
    
        如果它是'none'，补丁边界不会
        被画下来。
    
        对于未填充的标记，“edgecolors”kwarg
        被忽视并被迫在内部“面对”。
        '''

可视化决策边界

plt.figure()#初始化画布
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')#画散点图
plt.title('Dataset')#设置图像标题

nx, ny = 200, 100
x_min, x_max = plt.xlim()#获取或者是设定x座标轴的范围，当前axes上的x座标轴。
y_min, y_max = plt.ylim()#获取或者是设定y座标轴的范围，当前axes上的y座标轴。
x_grid, y_grid = np.meshgrid(np.linspace(x_min, x_max, nx),np.linspace(y_min, y_max, ny))
'''
#numpy.meshgrid()——生成网格点坐标矩阵。
#np.linspace主要用来创建等差数列
#numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)
start:返回样本数据开始点
stop:返回样本数据结束点
num:生成的样本数据量，默认为50
endpoint：True则包含stop；False则不包含stop
retstep：If True, return (samples, step), where step is the spacing between samples.(即如果为True则结果会给出数据间隔)
dtype：输出数组类型
axis：0(默认)或-1
'''
z_proba = lr_clf.predict_proba(np.c_[x_grid.ravel(), y_grid.ravel()])
'''
numpy.ravel()将多维数组拉平
np.c_np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等，类似于pandas中的merge()。
-------------------a------------------
[[1 2 3]
[4 5 6]]
-------------------b------------------
[[0 0 0]
[1 1 1]]
-------------------np.r_[a,b]--------------------
[[1 2 3]
[4 5 6]
[0 0 0]
[1 1 1]]
--------------------np.c_[a,b]-------------------
[[1 2 3 0 0 0]
[4 5 6 1 1 1]]
'''
z_proba = z_proba[:, 1].reshape(x_grid.shape)
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')#对网格中每个点的值等于一系列值的时候做出一条条轮廓线，类似于等高线 。
plt.show()

可视化预测新样本

plt.figure()#新画布
x_fearures_new1 = np.array([[0, -1]])#一个新的要预测的样本点
plt.scatter(x_fearures_new1[:,0],x_fearures_new1[:,1], s=50, cmap='viridis')
plt.annotate(s='New point 1',xy=(0,-1),xytext=(-2,0),color='blue',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))#对样本进行标注

x_fearures_new2 = np.array([[1, 2]])#一个新的要预测的样本点
plt.scatter(x_fearures_new2[:,0],x_fearures_new2[:,1], s=50, cmap='viridis')
plt.annotate(s='New point 2',xy=(1,2),xytext=(-1.5,2.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))

## 训练样本
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')

# 可视化决策边界
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')

plt.show()

关于annotate参考本链接内容

在训练集和测试集上分布利用训练好的模型进行预测

y_label_new1_predict=lr_clf.predict(x_fearures_new1)
y_label_new2_predict=lr_clf.predict(x_fearures_new2)
print('The New point 1 predict class:\n',y_label_new1_predict)
print('The New point 2 predict class:\n',y_label_new2_predict)
##由于逻辑回归模型是概率预测模型（前文介绍的p = p(y=1|x,\theta)）,所有我们可以利用predict_proba函数预测其概率
y_label_new1_predict_proba=lr_clf.predict_proba(x_fearures_new1)
y_label_new2_predict_proba=lr_clf.predict_proba(x_fearures_new2)
print('The New point 1 predict Probability of each class:\n',y_label_new1_predict_proba)
print('The New point 2 predict Probability of each class:\n',y_label_new2_predict_proba)
'''
输出：
The New point 1 predict class:
 [0]
The New point 2 predict class:
 [1]
The New point 1 predict Probability of each class:
 [[ 0.67507358  0.32492642]]
The New point 2 predict Probability of each class:
 [[ 0.11029117  0.88970883]]
 '''

基于鸢尾花（iris）数据集的逻辑回归分类实践

本次我们选择鸢花数据（iris）进行方法的尝试训练，该数据集一共包含5个变量，其中4个特征变量，1个目标分类变量。共有150个样本，目标变量为 花的类别 其都属于鸢尾属下的三个亚属，分别是山鸢尾 (Iris-setosa)，变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica)。包含的三种鸢尾花的四个特征，分别是花萼长度(cm)、花萼宽度(cm)、花瓣长度(cm)、花瓣宽度(cm)，这些形态特征在过去被用来识别物种。

变量	描述
sepal length	花萼长度(cm)
sepal width	花萼宽度(cm)
petal length	花瓣长度(cm)
petal width	花瓣宽度(cm)
target	鸢尾的三个亚属类别,‘setosa’(0), ‘versicolor’(1), ‘virginica’(2)

数据读取/载入

from sklearn.datasets import load_iris##我们利用sklearn中自带的iris数据作为数据载入，并利用Pandas转化为DataFrame格式
data = load_iris() #得到数据特征，data为一个字典类型，其中包括了['data', 'target', 'target_names', 'DESCR', 'feature_names']
print(data['DESCR'])#查看官方说明
iris_target = data.target #得到数据对应的标签
iris_features = pd.DataFrame(data=data.data, columns=data.feature_names) #利用Pandas转化为DataFrame格式

数据信息简单查看

特征数据

iris_features.info()
iris_features.head(5)
iris_features.tail()
iris_features.describe()

标签数据

pd.Series(iris_target).value_counts()#类似groupby函数功能

可视化描述

## 合并标签和特征信息
iris_all = iris_features.copy() ##进行浅拷贝，防止对于原始数据的修改
iris_all['target'] = iris_target
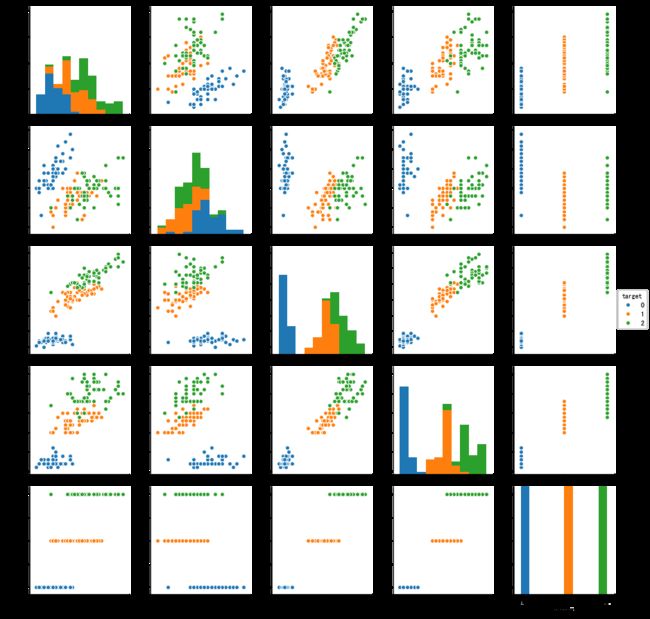
## 特征与标签组合的散点可视化
sns.pairplot(data=iris_all,diag_kind='hist', hue= 'target')
plt.show()

• 上图对角线直方图表示各列的分布情况
• 而非对角线上是两个不同属性之间的相关图
• • 不同的特征组合对于不同类别的花的散点分布，以及大概的区分能力，比如子图[4,2]
• 更多用法请点击本链接

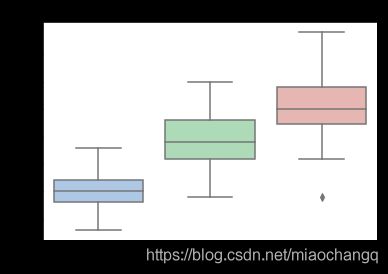
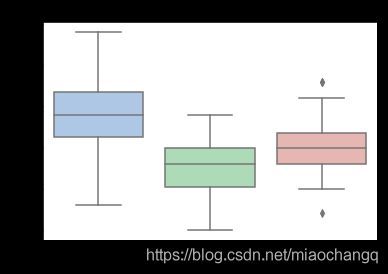
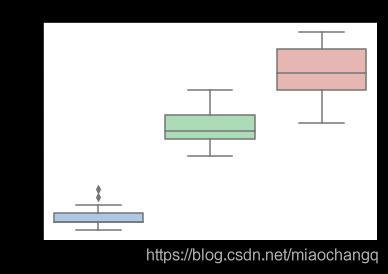
#逐变量绘制箱型图可以得到不同类别在不同特征上的分布差异情况。
for col in iris_features.columns:
    sns.boxplot(x='target', y=col, saturation=0.5, 
palette='pastel', data=iris_all)
    plt.title(col)
    plt.show()

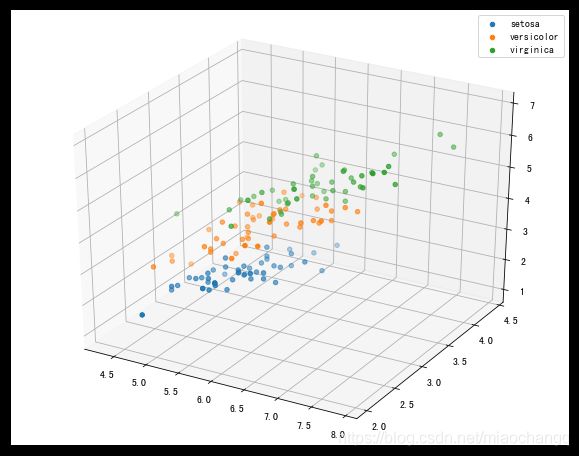
# 选取其前三个特征绘制三维散点图
from mpl_toolkits.mplot3d import Axes3D #导入3D坐标系

fig = plt.figure(figsize=(10,8))#初始画布
ax = fig.add_subplot(111, projection='3d')#添加子图

iris_all_class0 = iris_all[iris_all['target']==0].values#分类一
iris_all_class1 = iris_all[iris_all['target']==1].values#分类二
iris_all_class2 = iris_all[iris_all['target']==2].values#分类三
# 'setosa'(0), 'versicolor'(1), 'virginica'(2)
ax.scatter(iris_all_class0[:,0], iris_all_class0[:,1], iris_all_class0[:,2],label='setosa')
ax.scatter(iris_all_class1[:,0], iris_all_class1[:,1], iris_all_class1[:,2],label='versicolor')
ax.scatter(iris_all_class2[:,0], iris_all_class2[:,1], iris_all_class2[:,2],label='virginica')
plt.legend()#添加图例
plt.show()

利用 逻辑回归模型 在二分类上 进行训练和预测

数据集划分

##为了正确评估模型性能，将数据划分为训练集和测试集，并在训练集上训练模型，在测试集上验证模型性能。
from sklearn.model_selection import train_test_split
##选择其类别为0和1的样本（不包括类别为2的样本）
iris_features_part=iris_features.iloc[:100]
iris_target_part=iris_target[:100]
#前100样本为0，1类样本
#后50样本为2类样本
##测试集大小为20%，80%/20%分
x_train,x_test,y_train,y_test=train_test_split(iris_features_part,iris_target_part,test_size=0.2,random_state=2020)

模型训练

##从sklearn中导入逻辑回归模型
from sklearn.linear_model import LogisticRegression
##定义逻辑回归模型
clf=LogisticRegression(random_state=0,solver='lbfgs')
##在训练集上训练逻辑回归模型
clf.fit(x_train,y_train)
##查看其对应的w
print('the weight of Logistic Regression:',clf.coef_)

##查看其对应的w0
print('the intercept(w0) of Logistic Regression:',clf.intercept_)
#the weight of Logistic Regression: [[ 0.45244919 -0.81010583  2.14700385  0.90450733]]
#the intercept(w0) of Logistic Regression: [-6.57504448]
##在训练集和测试集上分布利用训练好的模型进行预测
train_predict=clf.predict(x_train)
test_predict=clf.predict(x_test)

评估分类结果

from sklearn import metrics
##利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))

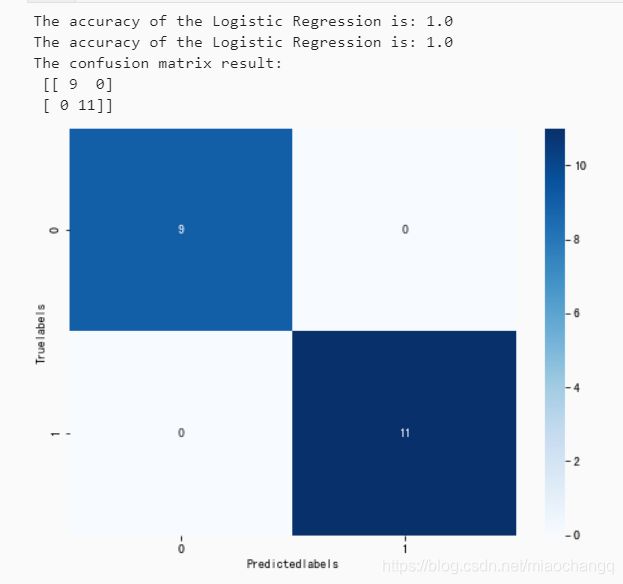
##查看混淆矩阵(预测值和真实值的各类情况统计矩阵)
confusion_matrix_result=metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)

##利用热力图对于结果进行可视化
plt.figure(figsize=(8,6))
sns.heatmap(confusion_matrix_result,annot=True,cmap='Blues')
plt.xlabel('Predictedlabels')
plt.ylabel('Truelabels')
plt.show()

利用 逻辑回归模型 在三分类(多分类)上 进行训练和预测

##测试集大小为20%，80%/20%分
x_train,x_test,y_train,y_test=train_test_split(iris_features,iris_target,test_size=0.2,random_state=2020)
##定义逻辑回归模型
clf=LogisticRegression(random_state=0,solver='lbfgs')
##在训练集上训练逻辑回归模型
clf.fit(x_train,y_train)
##查看其对应的w
print('the weight of Logistic Regression:\n',clf.coef_)
##查看其对应的w0
print('the intercept(w0) of Logistic Regression:\n',clf.intercept_)
##由于这个是3分类，所有我们这里得到了三个逻辑回归模型的参数，其三个逻辑回归组合起来即可实现三分类
##在训练集和测试集上分布利用训练好的模型进行预测
train_predict=clf.predict(x_train)
test_predict=clf.predict(x_test)
##由于逻辑回归模型是概率预测模型（前文介绍的p=p(y=1|x,\theta)）,所有我们可以利用predict_proba函数预测其概率

train_predict_proba=clf.predict_proba(x_train)
test_predict_proba=clf.predict_proba(x_test)

print('The test predict Probability of each class:\n',test_predict_proba)
##其中第一列代表预测为0类的概率，第二列代表预测为1类的概率，第三列代表预测为2类的概率。

##利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))
##查看混淆矩阵
confusion_matrix_result=metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)

##利用热力图对于结果进行可视化
plt.figure(figsize=(8,6))
sns.heatmap(confusion_matrix_result,annot=True,cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()

##The confusion matrix result:
##[[10  0   0]
##[0   8   2] 
##[0   2   8]]

'''
the weight of Logistic Regression:
 [[-0.43538857  0.87888013 -2.19176678 -0.94642091]
 [-0.39434234 -2.6460985   0.76204684 -1.35386989]
 [-0.00806312  0.11304846  2.52974343  2.3509289 ]]
the intercept(w0) of Logistic Regression:
 [  6.30620875   8.25761672 -16.63629247]
The test predict Probability of each class:
 [[  1.32525870e-04   2.41745142e-01   7.58122332e-01]
 [  7.02970475e-01   2.97026349e-01   3.17667822e-06]
 [  3.37367886e-02   7.25313901e-01   2.40949311e-01]
 [  5.66207138e-03   6.53245545e-01   3.41092383e-01]
 [  1.06817066e-02   6.72928600e-01   3.16389693e-01]
 [  8.98402870e-04   6.64470713e-01   3.34630884e-01]
 [  4.06382037e-04   3.86192249e-01   6.13401369e-01]
 [  1.26979439e-01   8.69440588e-01   3.57997319e-03]
 [  8.75544317e-01   1.24437252e-01   1.84312617e-05]
 [  9.11209514e-01   8.87814689e-02   9.01671605e-06]
 [  3.86067682e-04   3.06912689e-01   6.92701243e-01]
 [  6.23261939e-03   7.19220636e-01   2.74546745e-01]
 [  8.90760124e-01   1.09235653e-01   4.22292409e-06]
 [  2.32339490e-03   4.47236837e-01   5.50439768e-01]
 [  8.59945211e-04   4.22804376e-01   5.76335679e-01]
 [  9.24814068e-01   7.51814638e-02   4.46852786e-06]
 [  2.01307999e-02   9.35166320e-01   4.47028801e-02]
 [  1.71215635e-02   5.07246971e-01   4.75631465e-01]
 [  1.83964097e-04   3.17849048e-01   6.81966988e-01]
 [  5.69461042e-01   4.30536566e-01   2.39269631e-06]
 [  8.26025475e-01   1.73971556e-01   2.96936737e-06]
 [  3.05327704e-04   5.15880492e-01   4.83814180e-01]
 [  4.69978972e-03   2.90561777e-01   7.04738434e-01]
 [  8.61077168e-01   1.38915993e-01   6.83858427e-06]
 [  6.99887637e-04   2.48614010e-01   7.50686102e-01]
 [  5.33421842e-02   8.31557126e-01   1.15100690e-01]
 [  2.34973018e-02   3.54915328e-01   6.21587370e-01]
 [  1.63311193e-03   3.48301765e-01   6.50065123e-01]
 [  7.72156866e-01   2.27838662e-01   4.47157219e-06]
 [  9.30816593e-01   6.91640361e-02   1.93708074e-05]]
The accuracy of the Logistic Regression is: 0.958333333333
The accuracy of the Logistic Regression is: 0.8
The confusion matrix result:
 [[10  0  0]
 [ 0  7  3]
 [ 0  3  7]]
 '''

逻辑回归原理简介

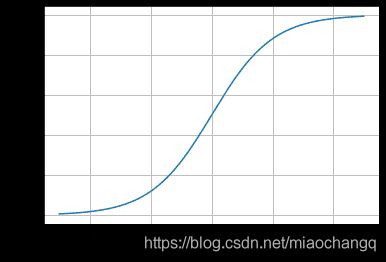
当z≥0 时,y≥0.5,分类为1，当 z<0时,y<0.5,分类为0，其对应的y值我们可以视为类别1的概率预测值。Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别），所以利用了Logistic函数（或称为Sigmoid函数），函数形式为：

$$\log (z)=1/(1+e^{-z})$$
对应的函数图像可以表示如下:

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-5,5,0.01)
y = 1/(1+np.exp(-x))

plt.plot(x,y)
plt.xlabel('z')
plt.ylabel('y')
plt.grid()
plt.show()

通过上图我们可以发现 Logistic 函数是单调递增函数，并且在z=0
而回归的基本方程，将回归方程写入其中为：
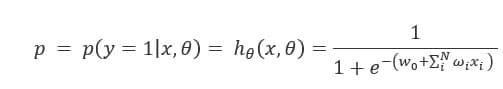所以，

逻辑回归从其原理上来说，逻辑回归其实是实现了一个决策边界：对于函数，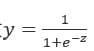
当z≥0 时,y≥0.5,分类为1，当 z<0时,y<0.5,分类为0，其对应的y值我们可以视为类别1的概率预测值。

对于模型的训练而言：实质上来说就是利用数据求解出对应的模型的特定的θ
。从而得到一个针对于当前数据的特征逻辑回归模型。
也就是对函数：
$$y={\theta }_0+{\theta }_1\ast x_1+{\theta }_2\ast x_2+...+{\theta }_n\ast x_n$$
已知所有的x和y的组合求θ
而对于多分类而言，将多个二分类的逻辑回归组合，即可实现多分类。