对于神经网络学习 Maxwell 方程的思考——泛化能力
对于神经网络学习 Maxwell 方程的思考——泛化能力
- 导言
- 1. 模型
- 2. 数据
- 3. 逐渐减少训练样本
- 3.1. 1615个训练样本
- 3.2. 155个训练样本
- 3.3. 27个训练样本
- 4. 逐渐增加训练样本
- 4.1. 1个训练样本
- 4.2. 2个训练样本
- 4.3. 均匀分布
- 4.4. 边缘分布
- 5. 均匀分布 VS 随机分布
- 5.1. 均匀分布
- 5.2. 随机分布
- 6. 结论
导言
最近在光学上兴起了 用神经网络学习 Maxwell 方程。最近试了试 Marin 他们提出的方法,对于一个 8 层膜正入射透射光谱,用 5万个样本作为训练集,使用 50 层 残差全链接网络。但是发现在某些区域,神经网络的预测结果也和实际结果不同。这说明 5万个样本作为训练集训练可能不够,应该有一个方法来确定如何选取训练集中的样本,使得数据集样本数最少,每个点都发挥它的最大作用。下面我们对 2 层膜正入射光谱,用 1万个样本作为训练集,使用 5 层全链接网络学习。
1. 模型
所使用的神经网络模型如何所示
input = tf.keras.Input(shape=(2), name='Input')
out1 = tf.keras.layers.Dense(500,activation='relu')(input)
out1 = tf.keras.layers.BatchNormalization()(out1)
out2 = tf.keras.layers.Dense(200,activation='relu')(out1)
out2 = tf.keras.layers.BatchNormalization()(out2)
out3 = tf.keras.layers.Dense(200,activation='relu')(out2)
out3 = tf.keras.layers.BatchNormalization()(out3)
output = tf.keras.layers.Dense(200,activation='linear')(out3)
model = tf.keras.Model(inputs=input, outputs=output)
2. 数据
总数据在下面的区域内均匀产生
d 1 : 0.1 ∼ 1 d_{1}:0.1 \sim 1 d1:0.1∼1
d 2 : 0.1 ∼ 1 d_{2}:0.1 \sim 1 d2:0.1∼1
但最终只选取 ( y − 0.55 ) 2 + ( x − 0.55 ) 2 = 0.04 (y-0.55)^{2}+(x-0.55)^{2}=0.04 (y−0.55)2+(x−0.55)2=0.04 这个圆内的数据作为数据集。
3. 逐渐减少训练样本
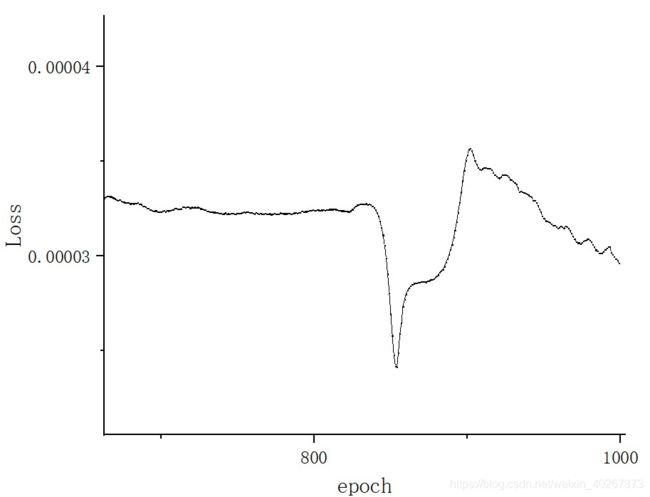
训练时 Loss 随周期下降如下图所示

最后几个周期 L o s s Loss Loss 如下图所示
3.1. 1615个训练样本
仅仅使用圆圈内的数据集(一共 1615个样本),最终在参数空间
d 1 : 0.1 ∼ 1 d_{1}:0.1 \sim 1 d1:0.1∼1
d 2 : 0.1 ∼ 1 d_{2}:0.1 \sim 1 d2:0.1∼1
中的 L o s s Loss Loss 如下图所示

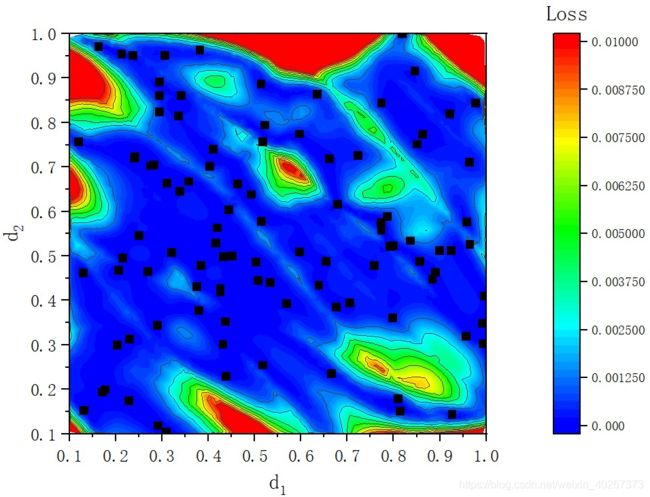
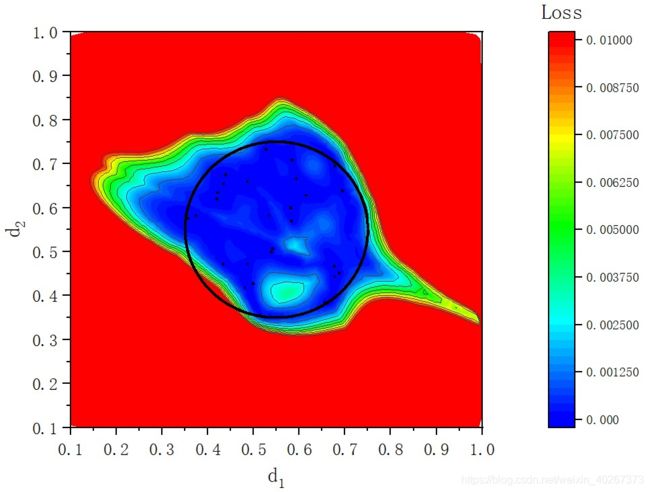
其中黑色的点是 使用作为训练集的数据样本。蓝色区域为神经网络预测结果很好的区域,红色区域为预测结果很糟糕的区域(这里使用 L o s s Loss Loss 0.01作为界限)
3.2. 155个训练样本
下面的结果是只使用 155 个圆圈内的数据点作为训练样本时的结果。
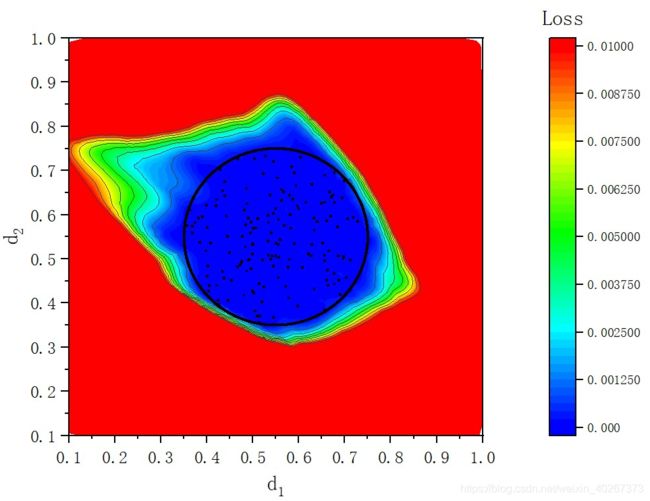
从上图中我们可以看到减少了训练样本后,撑开的空间仍然可以包含圆形区域。
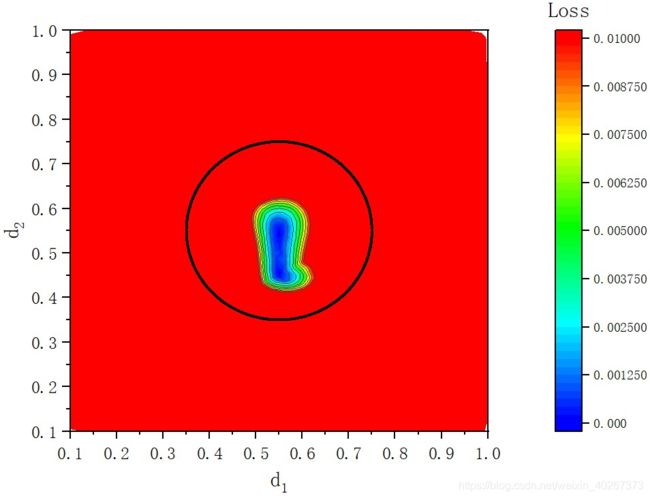
3.3. 27个训练样本
进一步减少训练数据会出现一个问题。样本数量太少导致,描述的区域可能不是一个圆形的区域,这使得圆形边缘数据量很少的区域变成红色。当样本数量较少时(在高维度时常常会面临的一个问题),随机生成数据将不再是一个合理的选择,如何生成数据使用尽可能少的点撑起的空间能覆盖整个圆呢?
4. 逐渐增加训练样本
4.1. 1个训练样本
当只有一个训练样本时,得到的结果如下图所示。可以看到一个样本只能撑起其周围的一小片区域。

4.2. 2个训练样本
对于两个相隔较远的训练样本来说,它们各自撑起了其周围的一小片区域。
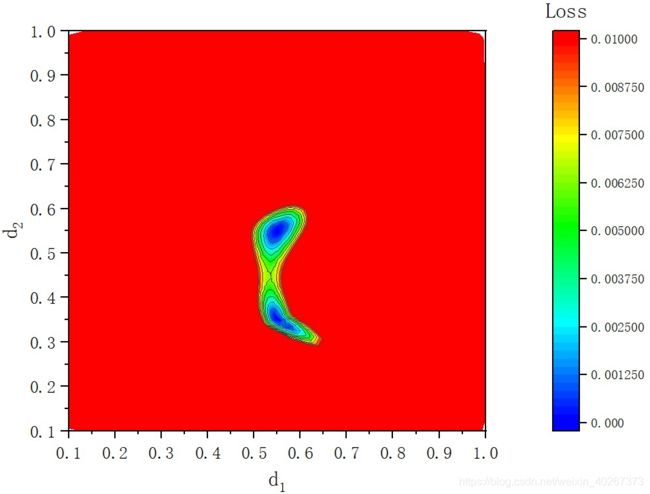
当着两个训练样本在参数空间中相隔较近时,两个区域会合成一个较大的区域。
由此我们可以猜想,最简单的使用最少的点撑开最大区域的方法为各个点均匀分布在参数空间中,且点与其最邻近的点之间的距离为 d = 0.1 d=0.1 d=0.1
4.3. 均匀分布
4.4. 边缘分布
仅仅在边缘处分布数据点,并不能撑起一片区域,除非其他地方的点足够多,可以将中间区域通过泛化来填充掉。但是从本文的第一章图可以看出即使有如此多的点,向四周泛化能力依旧有限。
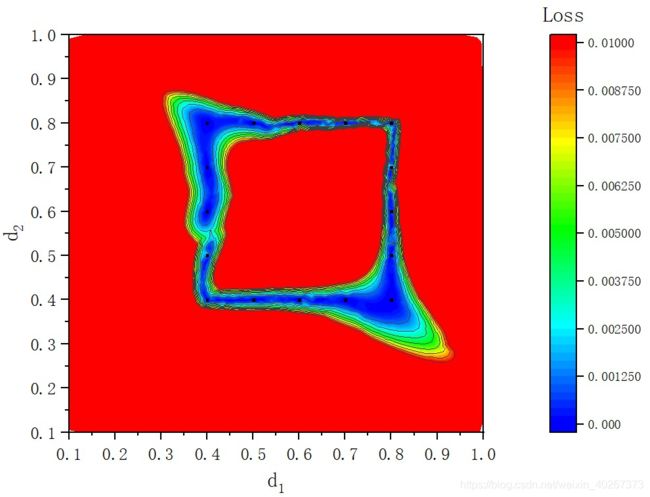
这告诉告诉我们只靠边界上的点并不能将中心的区域撑开。
5. 均匀分布 VS 随机分布
当点数足够多时,随机分布的效果和均匀分布的效果相当。但是当点数很少时,随机分布和均匀分布不在相同。特别是当参数空间维度足够高时,均匀分布和随机分布的效果需要进行详细讨论。例如:5万个训练样本对于一个 8 层膜的问题来说,也不过一个维度上平均只有 4 个数据点。
5.1. 均匀分布
下面,我们分别展示了 16 个数据点和 100 个数据点均匀分布时的情况。
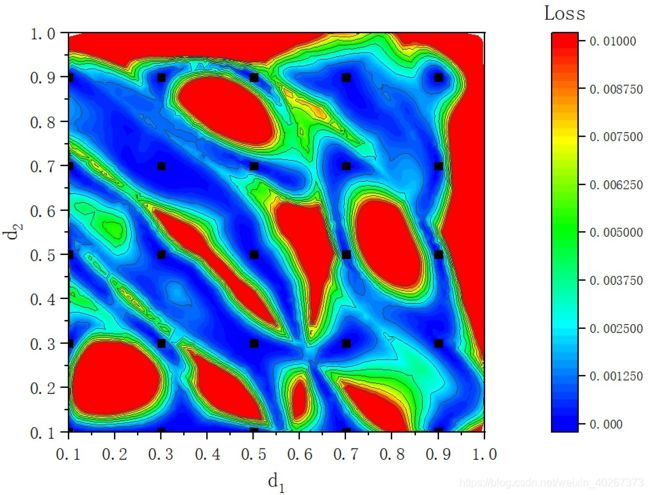
对于 16 个数据点来说,对于上述两层膜问题来说并不能很好的撑开我们关心的区域,会存在红色拟合效果并不好的区域。

对于 100 个均匀分布的数据点来说,可以很好的撑开我们关心的区域。
5.2. 随机分布
可以看到对于 100 个数据点来说,随机分布会出现有些地方并不能很好的撑开的情况。
6. 结论
在数据量较少时,均匀分布和随机分布并不等价。此时均匀分布的效果要比随机分布好。
对于高维问题来说,例如: 对于8层薄膜来说,5万个训练样本也仅仅相当于平均一个维度上只有 4 个数据点。故最好的方法为将5万个训练样本均匀分布而不是随机分布。对于一个20层薄膜来说,一个维度上4个数据点,那么训练样本数量将会达到 4 20 ≈ 1 0 12 4^{20} \approx 10^{12} 420≈1012 的量级。故对于高维问题来说,训练时使用的样本数量偏少是一个普遍存在的问题。使得我们需要思考如何在数据量较少的前提下,充分利用每一个数据且能检测该样本数量是否能很好的描述这个问题,撑开我们关心的区域。
在样本数量较少时,对于高维度问题来说,均匀分布可以截取一个平面来检测是否有没有撑开的区域,样本数量是否足够在我们关心的区域达到我们需要的精度。但是当样本数量较少时,随机分布不能给我们提供一种合理的方法进行检测。
当样本数量很多时,随机分布和均匀分布等价,即所有点均匀的分布在我们关心的参数空间中。