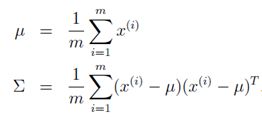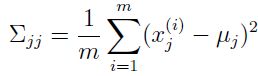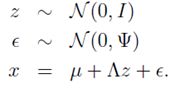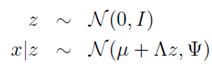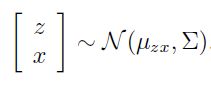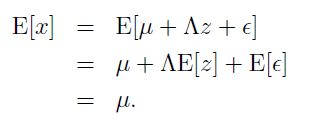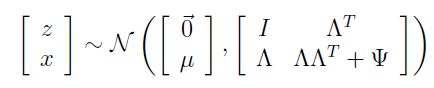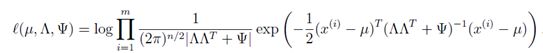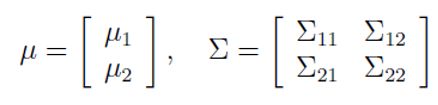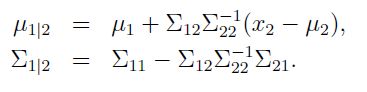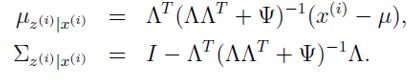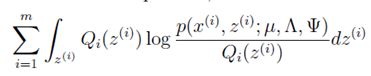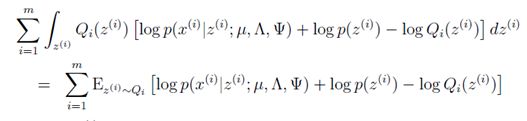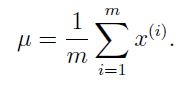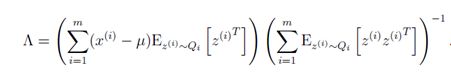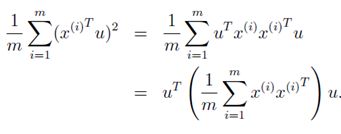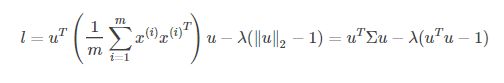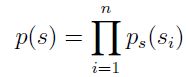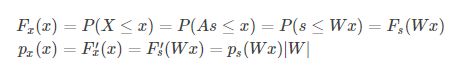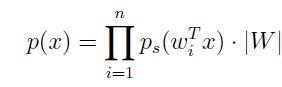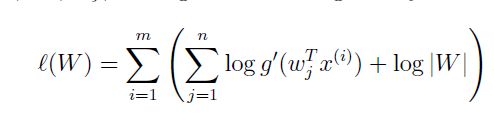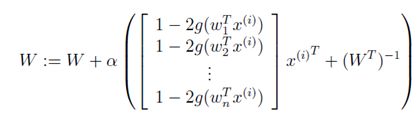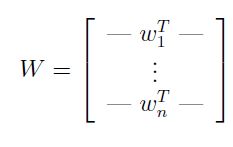因子分析_主成分分析_独立成分分析_斯坦福CS229_学习笔记
Part VIII 因子分析 主成分分析 独立成分分析
在上个部分介绍了EM算法，在此部分因子分析中，我们会再次应用到。
因子分析、主成分分析和独立成分分析都作为对于数据维度进行处理的手段，对于我们理解数据、更好的表示数据都起到或多或少的作用，因此将三者放在一起进行叙述。
目录
Part VIII 因子分析 主成分分析 独立成分分析
1 因子分析（Factor Analysis，FA）
1.1 背景
1.2 思想与推导
2 主成分分析（Principal Components Analysis，PCA）
3 独立成分分析（Independent Components Analysis,ICA）
4 小结
1 因子分析（Factor Analysis，FA）
首先介绍因子分析（FA）的提出背景，接着给出算法的思想，最后结合EM算法给出其参数的推导。
1.1 背景
之前介绍的各种算法，我们都有着一个不容忽视假设：样本的数量m足够充足，这样就使得通过训练（迭代），能够求解出参数从而构造出模型。但是现实有时候是残酷的，有时候会存在样本的数量匮乏的情况（m<
，根据极大似然法估计结果可得：
但是在当前样本数量m<
不存在且
。而上述两个值我们在接下来具体计算多元高斯分布时都会用到，这就使接下来的计算陷入了一个困境。有没有思路解决这种问题呢？当然有了，接下来介绍两种解决这种问题的思路。
但是先容插句话。有没有好奇在上述情况下（m<
则没有事儿。参考相关资料，发现并没有人提到。我的理解是，因为利用最大似然对于多元高斯模型进行估参时，得到的是无偏估计；而协方差阵则是有偏估计，且样本数据量越少，偏差越大。具体参考https://blog.csdn.net/qykshr/article/details/23273105。
现在回到正题。既然现在参数过多了，那么就可以对于参数加一些限制进行解决。最直接的思路便是通过限制协方差阵进行解决。例如可以限制协方差阵为对角阵。即：
这是一个很强的限制，因为这种限制认为各个参数之间是独立的，实际情况下是不可取的。在协方差阵为对角阵的基础之上，还可以进一步限制，即协方差阵中的对角元素取值相同。这两种强限制条件大多数情况下感觉都不太适用。
在没有限制条件即原有条件下，需满足
，才能保证非奇异；而在有上述两种限制条件下，只需要满足
，即可保证是非奇异矩阵。（这里并不明白，希望明白的大佬指点一下）。
实际情况下，各参数之间联系是存在并且是需要利用的。解决该问题也可以通过降维的方式进行，即将高维特征转为低维特征。
1.2 思想与推导
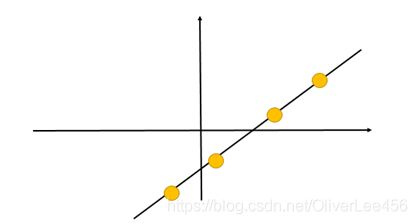
因子分析的思想在于，在多维数据x中，假设存在一些相对低维的潜在的变量z（即因子），高维数据x可通过低维潜在的z线性表示（因子分析的一个重要假设）。那么便可以根据此种变换将高维数据x映射到低维数据z，从而达到降维的目的。那么x和z存在着什么样的映射关系呢？因子分析做出以下假设来建立x和z的关系。
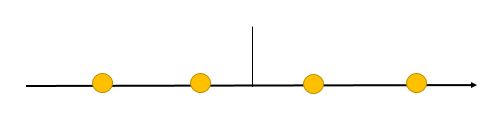
（1）低维空间中存在由高斯分布生成的m个k维变量（这又是因子分析的一个重要假设）。（图中m=4，k=1）
（2）原始数据空间x为n（图中n=2）维。可以将低维空间变量通过变换矩阵
（n*k）映射到x存在的高维空间。
（3）每个样本加上n维偏移向量
（4）每个样本加上n维高斯扰动ε~N(0,ψ)从而得到高维向量x
由上，可将因子分析模型总结如下：
从高维向量x可由潜在的低维高斯型向量z线性表示出发，存在着以下假设，并且在下列分布中隐变量z与随机高斯噪声
不相关：
第一行表示潜在型高斯变量分布。
第二行表示随机高斯噪声的影响。
第三行表示x由z线性表示形式。
结合上述定义，不难得到（确保明白这点）
接下来，对于x和z的联合分布建模。由于p(x,z)=p(x|z)*p(z)，两个高斯型密度函数的乘积仍然为高斯型，因此将x，z联合分布建模为高斯型如下：
之所以在左端写成矩阵形式，仅仅是为了接下来的表述方便。那么参数
和是什么形式呢？由多元高斯型联合分布和边缘分布的关系，我们不难进行以下推导：
因为
，因此
，又因为
，因此
那么就有：
接下来进行在的推导。在推导中需要利用概率论两个基本公式：
（1）若随机变量X，Y不相关，那么有EXY=EX*EY。在这里即为z与c不相关。
（2）
因为 
，那么我们可分别对于矩阵内元素进行如下计算：
![\Sigma _{zx}=\Sigma _{xz}=E[(z-E[z])(x-E[x])^{T}]=E[z(\mu +\Lambda z+\epsilon )^{T}]](http://img.e-com-net.com/image/info8/08f72172c6c84f7cb411c61201760290.gif){kind=small}
![=E[zz^{T}]\Lambda ^{T}+E[z\epsilon ^{T}]=\Lambda ^{T}](http://img.e-com-net.com/image/info8/7c4a703f1139456c941ad4540a3e422e.gif){kind=small}
![\Sigma _{xx}=E[(x-E[x])(x-E[x])^{T}]=E[(\mu +\Lambda *z+\epsilon )(\mu +\Lambda *z+\epsilon )^{T}]](http://img.e-com-net.com/image/info8/734882200cd34ec8bda5b06c39aee9ee.gif){kind=small}
![=\Lambda E[zz^{T}]\Lambda ^{T}+E[\epsilon \epsilon ^{T}]=\Lambda \Lambda ^{T}+\Psi](http://img.e-com-net.com/image/info8/ebb82032449641809d0a8702dcd3f702.gif){kind=small}
那么结合上述结果，即可得到x，z联合分布如下:
到这里就很清晰了。还是老套路，接下来利用最大似然法求解参数从而得到x，z的联合分布。此时参数为，和
。写出最大似然方程进行参数求解。
能够直接求偏导解出上述参数算你厉害。
此方程比较复杂，很难直接解出，因此就需要利用上一讲介绍EM算法进行求解了。在上一讲最后利用高斯混合模型对于EM算法的流程已经进行过介绍了。对于高斯混合模型而言，隐变量z为离散型，而在因子分析中隐变量z则为连续性；其实就是将求和改为积分即可。下面给出EM算法的解参数步骤：
（1）E-step：在E-step中，我们需要根据参数计算得到后验概率
。这里利用多元高斯分布的条件分布结论可直接推导出后验分布。先对于多元高斯分布的条件分布结论进行介绍。
若有二元高斯分布
，且参数如下表式：
那么可得以下结论：
，且
因此，根据此结论和前文的推导，可得后验分布
以上，E-step顺利走通。
（2）M-step：在M-step，我们要最大化：
简化此式得到：
然后分别对于参数
求偏导得到表达式如下所示（有兴趣的可以自己推推）：
在每次迭代中，更新参数的值直到收敛从而得到最终参数的结果。
由此，求解出三个参数，原有的n维（高维）空间样本x便可由k维（低维）空间隐变量z线性表示了。
2 主成分分析（Principal Components Analysis，PCA）
主成分分析（PCA）作为另外一种数据降维的手段得到了广泛的应用。
主成分分析的思想在于，在数据维度（n维）较大时，各个维度之间或多或少都会存在着相关性，而实际上我们并不需要全部使用维度进行处理，因为或许选取数据的某k维就代表了很大部分的n维特征。PCA的过程就是提取这k维的过程。
解释PCA可以从将近10种思路出发，这里选取比较好理解的最大方差的思路出发进行解释。
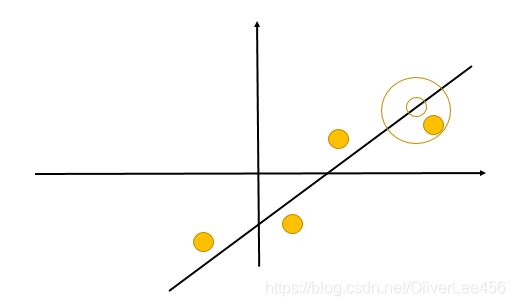
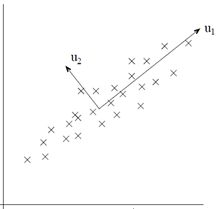
以2维数据压缩为1维数据为例，PCA要做的找到一个新的维度，是数据在新维度上的方差最大（即投影长度最长，如u1的方向所示）。因为根据信息论的观点，数据所包含的方差越大，那么数据所包含的信息量越大。如果新的投影方向u1能够包含原有数据的大部分信息（假设85%以上），那么可以认为在保证了数据信息的精度上进行了压缩。
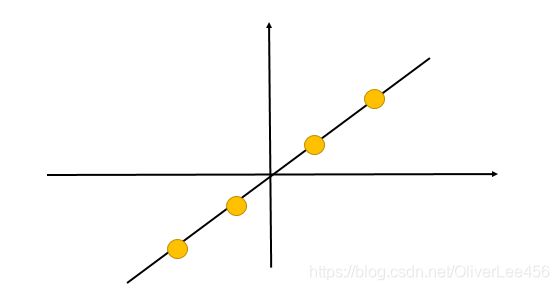
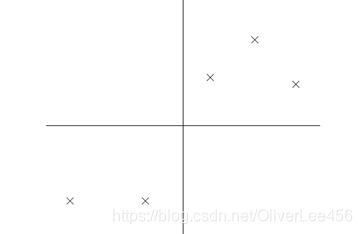
再举一个例子，假设原有5个2维样本如下图所示。
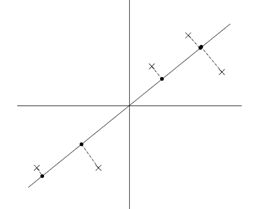
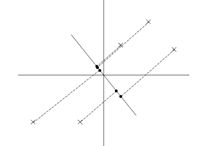
分别将原始数据按照如图所示的两个方向进行投影，得到左图与右图。
这就很清晰了，左图的数据明显比右图更能保留原始的数据信息。
那么包含了数据最多的新的投影方向是什么方向呢？听上去是一个解最值的问题，实际上也正是这样。
首先对于数据预处理。预处理的目的在于使各个维度的数据在接下来的处理中拥有着相同的尺度。预处理步骤如下。
（1）计算 
（2）更新 
，
（3）计算 
（4）更新 ，
经过预处理，每一维的数据都统一到均值为0，方差为1的这一分布尺度下了。
接下来定义优化问题，即寻找到投影长度最长的那个方向。
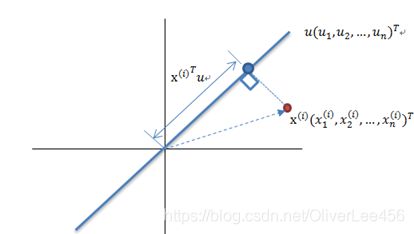
设样本空间存在单位方向向量u，那么某个样本点，在u上的投影长度 length 即为：
因此，优化问题即为在|u|=1的条件下，使下式最大化
利用拉格朗日乘数法即可解决，这里设
，即有下式：
对u求偏导，并另偏导等于0，得
，即
。
这不正好是一个特征方程嘛，u就是对应的特征向量，
即为特征向量对应的特征值。
竟是这么巧合？其实这也是可以理解的，从特征值与特征向量的意义出发，不难得到PCA要做的事情其实和直接求解其协方差阵的特征向量是一码事。因为目的都在于寻找到方差变化最大的方向（前k个方向）。而且由于协方差阵为对称阵，即得到的方向也相互正交，这就使得PCA的降维处理变得更纯粹。
回过头来，不难发现，特征值
代表着该特征向量对于原有信息的贡献率，特征值最大的一个 对应着的特征向量即为包含信息量最多的一个方向。因此我们要判断一个特征向量对于整体方差的贡献率，只需计算其特征值占全部特征值的比例即可。同理，要选取前k个特征向量组成新的维度空间，也根据k个特征向量的方差贡献率即可。
在此基础上，假设选取前k个特征向量进行降维，实现n维特征空间向k维转变，即可得到最终的映射关系：
3 独立成分分析（Independent Components Analysis,ICA）
独立成分分析的思想同样是为了将数据进行映射。
引入一个具体场景抛砖引玉—鸡尾酒宴会（cocktail party）。在宴会上，有n个人使用话筒同时在演讲。假设每个话筒（共计n个话筒）发出的声音是n个人的声音的和，那么如何从这n个话筒所记录的声音中区分中每个人的声音呢？这便是ICA的一个应用场景。
即可以将问题如下定义：设x（n*1维）为话筒最后发出的声音，s（n*1维）为每个人的声音，A（n*n）称为混合矩阵（mixing matrix），那么有以下关系 
。我们的目的在于解出s。设
,那么就有
。那么目的就转换为找到这个矩阵W。在没有任何先验知识的情况下，上述问题是不可解的。但是我们仍要探究下去。因此，同样是利用“老思路”解决此问题，即假设—建模—求参。
接下来给出ICA解决此问题的思路。
为了使问题可解，需要做一些假设：
（1）假设各个数据来源
相互独立。
（2）假设s的累积概率函数（Cumulative Distribution Function，CDF）作为先验知识可知。若不能根据经验确定，通常设做sigmoid函数效果会好一些。注意当设置为sigmoid函数为先验的CDF时，这同时也暗示着样本的均值为0，若样本的均值不为0，,则样本需要预处理将均值归为0。为什么设置sigmoid函数会带来这个影响呢？
这是因为，若设sigmoid函数 
，那么s的概率分布函数即为： 
。由于p（s）为偶函数，那么![E[s] = \int s*p(s)ds=0](http://img.e-com-net.com/image/info8/05385fe4240244cfa6348828e669fe62.gif){kind=small}
。.因此当假设s的分布函数为sigmoid函数后，如果x的均值不为0，需要进行归一化操作将其置为0。
（3） 的分布不能为高斯分布。具体原因参见讲义不再叙述。
接下来进行建模，由于 相互独立，因此由边缘分布乘积可直接得到联合密度函数：
又因为
，结合密度函数与分布函数的关系，可得：
从而推出：
接下来又到了求参环节了，这里我们的参数是W，同样利用最大似然法进行参数的求解。写出最大似然方程：
对W求偏导，可得每次迭代的更新公式为：
为了表述方便，可将解得的W写成如下形式：
根据W，那么原有数据中的每个信号的来源即可分离开了。即每个
。由此ICA从原有混合数据中将来源于不同信号源的数据进行分离的任务便完成了。
4 小结
或许有人会疑惑同样是作为数据降维的手段，好像最后的形式也差不多，因子分析（FA）和主成分分析（PCA）有什么区别呢？看完二者的推导，谈谈我的看法。
首先，差别还是挺明显的，二者的思想出发点就不同。FA是想从众多特征中找出一些共性（即隐变量z），利用共性对于原有数据进行表达；而PCA则是从众多特征中找出一些具有代表性的特征对于原有特征进行表达。
其次，二者的着重点也不一致。FA着重于各个变量间的协方差；而PCA则着重于总体的方差。
再者，FA相比较而言做了一些假设，较为受到限制；而PCA则无需假设，应用更广。
最后，PCA的实际应用范围是大于FA的。PCA在许多方面都发挥着不小的作用。
独立成分分析（ICA）的目的在于从多个信号混杂的数据中，解算出每个信号原有的数据。为此ICA做了一些假设，包括确定信号的分布函数。在ICA中应该留意，高斯分布的数据并不能直接应用ICA做分解。