CNN实战
1. 梯度计算
https://www.youtube.com/watch?v=LGA-gRkLEsI
https://marcovaldong.github.io/2016/05/16/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E4%B8%AD%E4%BD%BF%E7%94%A8%E7%9A%84%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C%E7%AC%AC%E5%85%AD%E8%AE%B2/
在训练时,我们是通过 w(t+1) = w(t) - ε Δw(t) 来进行参数更新的,其中Δw(t) 是反向传播回来的loss对参数的导数, ε是学习率,Δw(t) 是反向传播回来的loss对参数的导数。一般采用随机梯度下降法(SGD),为了解决计算效率问题,通过迭代的方法对梯度进行逼近,它只基于当前的batch进行参数更新,导致波动大,训练收敛慢,可能会收敛到一个比较烂的局部极小值。因此,我们可以根据实际情况,采用以下一些改进方法:
1)moum (动量法)
它将loss的梯度看成一种在地形图(解空间)转化势能的力对应的加速度, 梯度直接影响速度v,从而间接影响位置w。 在更新梯度时加上一个速度量v,使得训练更加平稳,更加容易收敛。计算公式是 v(t+1) = µ v(t) - εΔw(t) , w(t+1) = w(t) + v(t+1), 其中µ是动量系数, 物理意义是摩擦系数,用于抑制速度, µ值越大其保留的历史运动信息越多。µ也可以像调学习率那样在训练中进行调整,如在训练初期设置为0.5, 随着训练的进行增大该值,在训练末期设置为0.99。
2) Nesterov Momentum
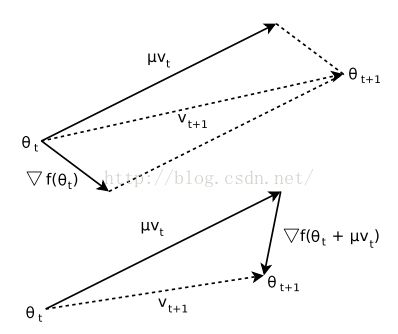
相对标准的Momentum法,梯度的计算从在更新v之前变成了更新v之后。如下图,它会先计算 w'(t+1) = w(t) + µ v(t) , 然后计算 v(t+1) = µ v(t) - ε Δw‘(t+1) , 最后更新 w(t+1) = w(t) + v(t+1) 。
3)二阶方法
基于牛顿法可以进行更好的优化求解,公式为, 其中Hf(x)是hessian阵,是损失函数的二阶偏导数,表示损失函数的局部曲率。但是Hessian阵的计算量和内存消耗是非常大的,使得其在DL中无法应用,即使有拟牛顿法L-BFGS, 但也没有基于mini-batch做出比SGD更好的效果。
2) RMSprop.
当训练遇到一些“烂”的(outlier)batch时,比如我们梯度一直是+0.001左右,突然来了个-0.009, 则会破坏梯度。因此,采用每次计算的梯度将除以最近一次梯度的均方根的方法进行正则化,使得梯度更加平稳。但它有可能导致收敛缓慢。
3) AdaGrad (自适应梯度法)
这是一种相对于RMSprop更暴力的方法。它利用的是全部历史的梯度信息进行当前梯度计算。
4) Adam (adaptive moment estimation)
这是一种一阶梯度优化方法,它基于低阶动量自适应估计。计算复杂度和内存消耗较低,适合非平稳或大量噪声的情况。不同的参数各自通过估计梯度的第一、第二动量,计算自适应学习率。这种方法结合了AdaGrad和RMSProp两者,前者对稀疏梯度表现较好,后者在非平稳情况下表现较好。它的优点是参数更新的大小对梯度的rescale是无关的,无须平稳的目标,对稀疏梯度也表现不错,而且不用显式调整学习率。在训练后期,隐层单元逐渐稳定在特定的模式下,使得梯度逐渐稀疏 , β2可以变大些(The best results were achieved with small values of (1−β2) and bias correction; this was more apparent towards the end of optimization when gradients tends to become sparser as hidden units specialize to specific patterns.)
weight_decay
这是用于控制损失函数中的规则项对损失的影响程度,在caffe中,可以分别控制每层的参数的decay。
2. 模型合成
通过把多个较好的模型进行融合,往往可以获得更好的结果。http://cs231n.github.io/neural-networks-3/
2. ReLU/PReLu
3. xavier
4. 3x3
5. 观察
给NN一点时间, 要根据任务留给NN的学习一定空间. 不能说前面一段时间没起色就不管了. 有些情况下就是前面一段时间看不出起色, 然后开始稳定学习.
6. batch size
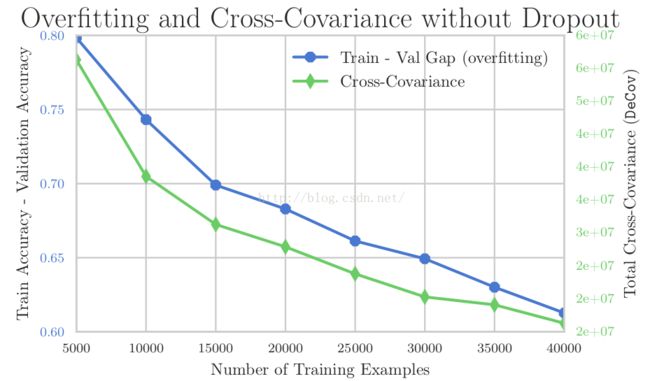
提高CNN的方法其中重要的一点是scale,具体方法包括batch normalization, Adaptive SGD , ReLu, 从而获得更佳的收敛性能。另外,防止overfitting(过拟合)也是非常重要的一个课题。有研究者挖掘出了训练数据量、训练测试差别、互协方差之间的关系,如下图
方法包括
1)regularizing the norm of the weights (Tikhonov, 1943) Lasso (Tibshirani, 1996),
2)Dropout (Srivastava et al., 2014), 为防止神经元之间的信息互相依赖(即存在这样的两个或更多的隐藏节点,它们依赖其它的节点来进行函数拟合),通过在训练期间随机选取神经元激活置为0来获得不同的模型并进行平均, 降低了特征间互相关,提高了泛化能力和稀疏性。
3)Drop-Connect (Wan et al., 2013),
4)Maxout (Goodfellow et al., 2013)
5) DeCov. (2016). 通过鼓励激活单元之间的去相关来设计一种loss,这种loss用来惩罚特征的冗余,对相同的特征表达进行去相关。
关于方法轮,可以看我翻译的deeplearning_book的第11张:深度学习实战11章中文版
【TODO修正】