CRF(条件随机场)知识整理

CRF(条件随机场)知识整理

  HMM建模序列学习问题时，由于引入了状态序列的马尔可夫性假设，限制了上下文特征的提取，相比之下，条件随机场(CRF)模型可以提供更多的上下文信息，且相比最大熵模型(MEM)，它也有效规避了标记偏置问题（具体请查看最大熵模型相关资料）。

一、马尔科夫网络

  在马尔科夫链中，随机变量在时间上顺序产生，构成一个随机过程，那么，能不能将马尔科夫链的概念扩展到空间上呢？假设存在一组随机变量，它们之间存在着一些边连接，是否能假设它们所满足的马尔科夫性呢？

1.1 无向图和团

  我们先简要回顾无向图的一些概念，在图论中，图由节点(node)集合和边(edge)集合构成，记作$G=(V,E)$，$V=\{x_1,\dots ,x_n\}$表示顶点集合，$E=\{(x_i,x_j)|x_i\to x_j\}$为边集合，$x_i\to x_j$表示节点$x_i$能到达节点$x_j$，在无向图中有$x_i\to x_j$等价于$x_j\to x_i$。
  完全图指任意节点之间均存在一条边连接的无向图。一个无向图的子图指图节点集合和边集合的子集。无向图的完全子图称为一个团（clique）。
  对于团，我们可以定义其节点上的非负函数，称为势函数。引入符号，记图$C=(V_1,E_1)$为一个团，其中$V_1=\{x_1,\dots ,x_n\}$为节点变量，定义非负函数${\varphi }_c(x_1,\dots ,x_n)$，它称为团$C$的势函数或势能函数，简记作${\varphi }_c({\mathbf{x}}_c)$。
  到这里，可能会有些疑惑，势函数究竟具有怎样的物理意义呢？我个人理解，势函数描述了网络处于某种状态时的某一指标，可能是能量，如果将网络节点视为随机变量，并对势函数做归一化处理，也可将其视作概率。

1.2 马尔科夫网络的概念

  现在，我们来回答本部分一开始提出的问题，在马尔科夫链中，我们假设的马尔科夫性认为当前时刻的随机变量分布仅与上一时刻的随机变量相关，如果给定一个无环网络，每个节点均代表一个随机变量，我们是否可假设该节点的概率分布仅与其邻居节点相关呢？这样，我们就得到了马尔科夫网络的基本定义，给定一个由随机变量构成的网络$G=(V,E)$，节点$x_i\in V$的条件分布满足：
$$p(x_i|G\setminus \{x_i\})=p(x_i|N_i)$$
这里，$N_i$表示节点$x_i$的邻居节点集。那么，马尔科夫网络这样的性质带来了怎样的好处和便利呢？我们先来看一种新颖的分布函数。

1.3 吉布斯分布(Gibbs distribution)

  上面提到过，团的势函数经过归一化后可以视为一种概率分布，现在我们来具体审视这种观点。同样，我们给定一个无环的随机网络（节点是随机变量）$G$，它可以分解为一些团（事实上都可以做到），团集合记作$C=\{c_1,\dots ,c_m\}$。在其上定义势函数$\{{\varphi }_{c_1}({\mathbf{x}}_{c_1}),\dots ,{\varphi }_{c_m}({\mathbf{x}}_{c_m})\}$，则函数
$$\Phi (G)=\frac{1}{{\mathbf{Z}}_{\varphi }}\prod _{i=1}^m{\varphi }_{c_i}({\mathbf{x}}_{c_i})$$
称为吉布斯分布。
这里，记$\mathbf{x}={\mathbf{x}}_{c_1}\cup \cdots \cup {\mathbf{x}}_{c_m}$，
$${\mathbf{Z}}_{\varphi }=\sum _{\mathbf{x}}\prod _{i=1}^m{\varphi }_{c_i}({\mathbf{x}}_{c_i})$$
为归一化因子。

1.4 Hammersley-Clifford定理

  下面我们来探究马尔科夫网络和吉布斯分布之间的关系。事实上，正如转移矩阵和初始分布完全描述了马尔科夫链的概率信息，吉布斯分布描述了马尔科夫网络的概率信息，我们自然要问，是不是任意给定的马尔科夫网络都能找到一个吉布斯分布与之对应？如果一个网络存在吉布斯分布，那么这个网络是否是马尔科夫网络呢？答案是肯定的，Hammersley-Clifford定理证明了马尔科夫网络和吉布斯分布之间的等价关系，该定理的证明过于复杂，请参考HC定理证明。

二、条件随机场的概念

  上述马尔科夫网络又称作马尔科夫随机场。它考虑的是联合分布，而在序列学习问题中，我们通常都是给定观测序列，求状态序列的分布，因而，能否对条件分布也做类似假设呢？

2.1 一般定义

  如果对条件分布也做类似假设，我们便得到了条件随机场的基本概念。与马尔科夫随机场不同的是，在条件随机场中我们考虑两组随机变量集，记为$Y$和$X$，且$Y$构成一个随机网络$G$，我们对条件分布$p(Y|X)$做如下假设，
$$p(Y_v|X,G\setminus Y_v)=p(Y_v|X,Y_w\in N_v)$$
这一假设类似于马尔科夫随机场中的假设，不同的是给定了另一组随机变量$X$，我们大可不必理会它的作用，将其看做具有确定的状态即可。

2.2 线性链条件随机场

  在NLP中，我们依然习惯于构建链式的模型，这一模型更适合于序列学习的情境，且具备更少的参数。基本假设如下
$$p(Y_i|X,Y\setminus Y_i)=p(Y_i|X,Y_{i-1},Y_{i+1})$$
  在线性链条件随机场中，我们可以考虑更加简单的团和势函数形式，最简单的团有$Y_{i-1}$和$Y_i$构成，我们定义的势函数也具备更加简单的形式，即$\varphi (Y_{i-1},Y_i,X)$，注意这里由于是关于$X$的条件分布，所以所有势函数都是关于整个序列$X$的函数。条件随机场的结构图如下，

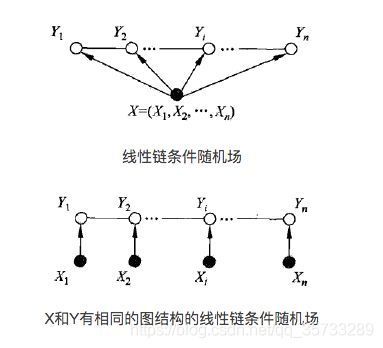
  接下来，我们引入条件随机场（在接下来的部分，我们使用术语“条件随机场”时默认为“线性链条件随机场”）的吉布斯分布，这一过程称为参数化，我们重新规范以下符号以便于和序列学习中的符号一致，设标记序列为$\mathbf{s}=\{s_1,\dots ,s_T\}$，其中$s_t\in S$，观测序列为$\mathbf{o}=\{o_1,\dots ,o_T\}$，其中$o_t\in W=\{w_i\}{|}_{i=1}^N$，则吉布斯分布为，
$$p(\mathbf{s}|\mathbf{o})=\frac{1}{Z_o}\exp \left[\sum _{t=1}^T\sum _k{\lambda }_k{f}_k(s_{t-1},s_t,\mathbf{o},t)\right]$$
这里，$$Z_o=\sum _{\mathbf{s}\in S^T}\exp \left[\sum _{t=1}^T\sum _k{\lambda }_k{f}_k(s_{t-1},s_t,\mathbf{o},t)\right]$$为归一化因子，$f_k(s_{t-1},s_t,\mathbf{o},t)$称为特征函数，${\lambda }_k$是权重参数，它是定义势函数的关键所在，接下来，我们探讨一下特征函数的具体含义。

2.3 特征函数

  要想理解特征函数，我们需要从标记序列和观测序列本身的含义考虑，也就是说在不同的模型应用场景下，特征函数的定义有着不同的方法，我们这里拿命名实体识别（NER）任务来举例，这一任务中，观测序列为单词序列，标记序列为当前词汇所属的命名实体类别（例如地区、人名、非实体等）。通常我们将特征函数定义为二值函数，简单来说，就是当$s_{t-1},s_t$满足某一条件且观测序列$\mathbf{o}$满足某一条件时，取1，否则取0。根据标记序列是否存在上下文联系，我们将特征函数又可以分类为两类，一类是Unigram特征，该特征和观测序列以及当前的状态$s_t$相关；另一类是Bigram特征，该特征和观测序列以及$s_{t-1}$和$s_t$均相关。即
$$\sum _k{\lambda }_k{f}_k(s_{t-1},s_t,\mathbf{o},t)=\sum _k{\mu }_k{l}_k(s_{t-1},s_t,\mathbf{o},t)+v_k{m}_k(s_t,\mathbf{o},t)$$
举一个具体的例子，有如下一个简单的标记序列和观测序列，

“Confidence in the pound is widely expected”
“B O B I O O O”

第一行为观测序列，第二行为标记序列，我们可以定义如下的一个特征函数，
$v(s_t,\mathbf{o},t)=1$，若$s_t=$’B’且$o_t=$’Confidence’，否则为0。类似的，我们可以对词典中的每个单词都定义一个类似的特征函数。因此，给定一个语料库，我们无法给出所有特征函数的具体形式，但我们可以给出特征模板（具体请查看CRF++框架的使用教程）并且增加一个特征筛选程序。

  显然，在定义了特征函数后，我们下一步需要做的就是推导CRF的训练过程。

三、前向后向算法

  同样，条件随机场也面临组合爆炸的问题，但幸运的是条件随机场与隐马尔科夫模型之间存在结构相似性，于是我们考虑是否可以类似地定义前向变量和后向变量，用动态规划的方法来简化计算

3.1 前向向量

  与HMM理论不同的是，在CRF中我们参数化了概率分布，推导的基本技术是吉布斯分布和团分解，在分布函数里，归一化因子$Z_o$看起来似乎非常难以处理，由于它是一个常数，我们可以暂时不考虑它。
  值得注意的是，在CRF理论中同样存在着状态（标签）的转移，因而我们是否可以类似地定义一个状态转移矩阵呢？答案是显然的，引入下面的符号
$$M_t(y_i,y_j|\mathbf{o})=\exp \left[\sum _k{\lambda }_k{f}_k(s_{t-1}=y_i,s_t=y_j,\mathbf{o},t)\right]$$
它代表了非归一化的转移概率，简记为$M_t(\mathbf{o})$。当然，为了书写方便，这里我们将两种特征函数合并。为了规范化，我们在原序列$\mathbf{s}$中引入两个额外标记$s_0$和$s_{T+1}$，其状态索引分别为start和stop。我们定义一个向量序列${\alpha }_t(\mathbf{o})\in {\mathbb{R}}^N$，$N$为标签数，当$t=0$时，其第$i$个元素${\alpha }_0(i|\mathbf{o})$满足满足
$${\alpha }_0(i|\mathbf{o})=\{\begin{array}{rl}& 1,i=start\\ & 0,other\end{array}$$
且${\alpha }_t(\mathbf{o})$满足如下的迭代式，
$${\alpha }_t(\mathbf{o})={\alpha }_{t-1}(\mathbf{o})M_t(\mathbf{o})$$
  稍加分析可知，${\alpha }_t(j|\mathbf{o})$的概率意义是非规范化的${\sum }_{s_1,\dots ,s_{t-1}}p(s_1,\dots ,s_{t-1},s_t=y_j|\mathbf{o})$。事实上，上面的递推式之所以成立，其本质是由吉布斯分布的形式决定的。上述向量${\alpha }_t(\mathbf{o})$称为前向向量。

3.2 后向变量

  类似地，我们定义后向向量${\beta }_t(\mathbf{o})$，其初始化为
$${\beta }_{T+1}(i|\mathbf{o})=\{\begin{array}{rl}& 1,i=end\\ & 0,other\end{array}$$
它的递推式为
$${\beta }_t(\mathbf{o}{)}^T=M_{t+1}(\mathbf{o}){\beta }_{t+1}(\mathbf{o})$$
稍加分析，其概率意义为${\sum }_{s_{t+1},\dots ,s_{T+1}}p(s_t=y_j,s_{t+1},\dots ,s_{T+1}|\mathbf{o})$。

3.3 归一化因子的计算

  接下来，我们考虑归一化因子$Z_o$的计算，根据前向向量的定义，有
$${\alpha }_{T+1}(\mathbf{o})={\alpha }_0(\mathbf{o})M_1(\mathbf{o})\dots M_{T+1}(\mathbf{o})$$
且${\alpha }_{T+1}(\mathbf{o})$具有概率意义${\sum }_{\mathbf{s}\in S^T}p(\mathbf{s},s_{T+1}=y_j|\mathbf{o})$，而我们又知道$s_{T+1}=y_{stop}$，因而${\alpha }_{T+1}(\mathbf{o})$的第$stop$个元素应当被归一化为1，也就是说矩阵
$$M_1(\mathbf{o})\dots M_{T+1}(\mathbf{o})$$
的$(start,stop)$处的元素为归一化因子，记作
$$Z_o={\left(M_1(\mathbf{o})\dots M_{T+1}(\mathbf{o})\right)}_{(start,stop)}$$
  有了归一化因子的计算，我们能够推得下面这个重要结论，
$$\begin{array}{rlr}p(s_t=y_i|\mathbf{o})& =\sum _{s_1\dots s_{t-1},s_{t+1},\dots ,s_T}p(\mathbf{s}|\mathbf{o})& =\frac{{\alpha }_t(i|\mathbf{o}){\beta }_t(i|\mathbf{o})}{Z_o}\end{array}$$
  至此，训练模型前的一些准备工作已经完毕。

四、参数估计

  接下来我们推导参数估计的方法，与HMM不同的是，CRF的训练是有监督的，即同时给定了训练集$\{(\mathbf{s},\mathbf{o})\}$。

4.1 参数梯度

  我们首先构造如下的对数似然函数，其中参数为$\Lambda =({\lambda }_1,\dots ,{\lambda }_k,\dots )$
$$\begin{array}{rl}L(\Lambda )& =\log p(\mathbf{s}|\mathbf{o})\\ & =\sum _{t=1}^T\sum _k{\lambda }_k{f}_k(s_{t-1},s_t,\mathbf{o},t)-\log (Z_o)\end{array}$$
为了减少过拟合，我们这里引入$l_2$正则项，当然，也可以引入$l_1$正则。于是，有
$$L(\Lambda )=\sum _{t=1}^T\sum _k{\lambda }_k{f}_k(s_{t-1},s_t,\mathbf{o},t)-\log (Z_o)-\sum _k\frac{{\lambda }_k^2}{2{\sigma }^2}$$
现在，我们求偏导数，得
$$\frac{\partial L}{\partial {\lambda }_k}=\sum _{t=1}^T{f}_k(s_{t-1},s_t,\mathbf{o},t)-\sum _{t=1}^{T}p(\mathbf{s}|\mathbf{o})f_k(s_{t-1},s_t,\mathbf{o},t)-\frac{{\lambda }_k}{{\sigma }^2}$$
引入期望的记号，上式第一项为
$$E[f_k]=\sum _{t=1}^T{f}_k(s_{t-1},s_t,\mathbf{o},t)$$
第二项为，
$$E_{\mathbf{s}|\mathbf{o}}[f_k]=\sum _{t=1}^{T}p(\mathbf{s}|\mathbf{o})f_k(s_{t-1},s_t,\mathbf{o},t)$$
因此，梯度可以简记为
$$\frac{\partial L}{\partial {\lambda }_k}=E[f_k]-E_{\mathbf{s}|\mathbf{o}}[f_k]-\sum _k\frac{{\lambda }_k}{{\sigma }^2}$$
由于$p(\mathbf{s}|\mathbf{o})$的存在，上面的梯度很难求零点，因而也就难以得出CRF解的解析形式。

4.2 优化算法

  需要说明的是，CRF的似然函数为凸函数，因而存在全局最优，我们考虑利用数值算法进行求解，比较快速的是牛顿法，但由于这里参数较多，内存开销较大，因而考虑拟牛顿法，性能较好的是L-BFGS算法，其基本原理可以参考我的另一个博客L-BFGS优化算法基本原理，它类似于一个黑盒子，需要传入变量值和梯度值就可以进行迭代运算。

五、可用的工具

  CRF++是一个比较轻量级，速度也较快的线性链条件随机场工具，由C++语言实现，同时具有python接口。

[参考资料]
[1]: John Lafferty, Andrew McCallum, Fernando Pereira.Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data