对条件随机场CRF（Conditional Random Field）的理解

一、图的定义

我们用$G$代表图，图是由结点和边组成，即：$G=（V，E）$，其中$V$代表结点的结合，$E$代表边的结合。

例如上图$G$中：

• $V$由结点a、结点b、结点c、结点d组成，即：$V=｛a,b,c,d｝$
• $E$由边ab、边ac、边bd、边cd组成，即：$E=｛e_{ab},e_{ac},e_{bd},e_{cd}｝$

在CRF中，每一个结点代表一个随机变量，每条边代表变量之间的一种依赖关系。在CRF中，只研究无向图，也就是边上没有箭头。

二、三个性质

在马尔科夫随机场中，随机变量（结点）需要满足以下三个性质，即成对的马尔科夫性、局部的马尔科夫性、全局的马尔科夫性，接下来依次介绍。

1. 成对的马尔科夫性

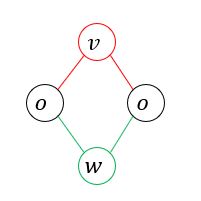
如图，假设随机变量$v$和随机变量$w$之间是没有关系的（也就是$v$和$w$之间没有边直接相连），其他的除了$v$和$w$之外的随机变量，用$o$来表示。那么成对的马尔科夫性就可以表示成以下的公式：
$$P(Y_v,Y_w|Y_o)=P(Y_v|Y_o)\cdot P(Y_w|Y_o)$$在随机变量$o$的条件下$v和w$的联合概率等于在$o$的条件下$v$的概率乘以在$o$的条件下$w$的概率。也就是说随机变量$v$和随机变量$w$在随机变量$o$的条件下，是相互独立的，因为它们没有边直接相连，这就是成对马尔科夫性的意思。

2. 局部的马尔科夫性

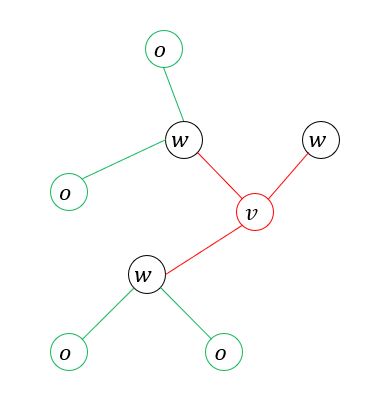
如图，假设随机变量$v$和随机变量$o$之间是没有关系的（也就是$v$和$o$之间没有边直接相连），其他的除了$v$和$o$之外的随机变量是$w$。那么局部的马尔科夫性就可以表示成以下的公式：
$$P(Y_v,Y_o|Y_w)=P(Y_v|Y_w)\cdot P(Y_o|Y_w)$$在随机变量$w$的条件下$v和o$的联合概率等于在$w$的条件下$v$的概率乘以在$w$的条件下$o$的概率。也就是说随机变量$v$和随机变量$o$在随机变量$w$的条件下，是相互独立的，因为它们没有边直接相连，这就是局部马尔科夫性的意思。

3. 全局的马尔科夫性

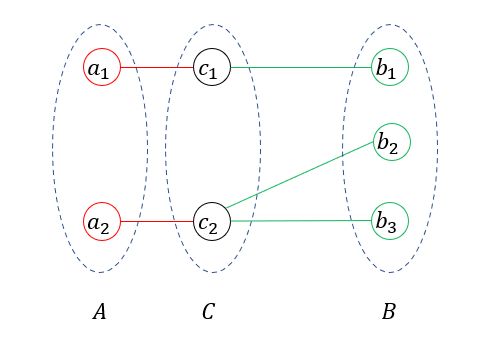如图，可以看到$A$集合的随机变量$a_1$、$a_2$与$B$集合的随机变量$b_1$、$b_2$、$b_3$没有任何关系，也就是$A$和$B$中的随机变量彼此之间没有边直接相连,被$C$在中间隔开了。那么全局的马尔科夫性就可以表示成以下的公式：
$$P(Y_A,Y_B|Y_C)=P(Y_A|Y_C)\cdot P(Y_B|Y_C)$$在随机变量$C$的条件下$A和B$的联合概率等于在$C$的条件下$A$的概率乘以在$C$的条件下$B$的概率。也就是说随机变量$A$和随机变量$B$在随机变量$C$的条件下，是相互独立的，因为它们没有边直接相连，这就是全局马尔科夫性的意思。

如果一个图$G$中的随机变量（结点）满足以上三个性质，则称之为概率无向图模型，也叫做马尔科夫随机场。
（以上三个性质可以相互推导）

三、团的定义

在一个无向图中，任意两个随机变量，它们之间都有边相连，这个图就称为一个团。例如：

以上的图中存在的团有：

• 两个随机变量的：$（Y_1,Y_2）（Y_1,Y_3）（Y_2,Y_3）（Y_2,Y_4）（Y_3,Y_4）$
• 三个随机变量的：$（Y_1,Y_2,Y_3）（Y_2,Y_3,Y_4）$

我们发现$Y_1和Y_4$构不成团，它们之间没有边相连，同理$Y_1{Y}_2{Y}_3{Y}_4$也构不成团，也是因为$Y_1和Y_4$之间没有边相连。

最大团定义：一个团中随机变量数目已经是最多的，如果再加一个随机变量，它就不能再构成一个团了。

上面的例子的最大团就是$（Y_1,Y_2,Y_3）（Y_2,Y_3,Y_4）$ 2个，$（Y_1,Y_2,Y_3）$中如果加入$Y_4$，便构不成团了，$Y_1和Y_4$之间没有边相连，所以只能是$（Y_1,Y_2,Y_3）$。

四、概率无向图模型(马尔科夫随机场)

概率无向图模型的联合概率分布可分解为在最大团上的随机变量函数$\psi ()$的乘积，表示为以下形式：
$$P(Y)=\frac{1}{Z}\cdot \prod _C{\psi }_C(Y_C)$$

• $C$代表的就是每一个最大团，在上节例子中也就是$（Y_1,Y_2,Y_3）（Y_2,Y_3,Y_4）$
• ${\psi }_C(Y_C)$代表最大团的随机变量函数，上节例子中有2个最大团，也就有2个最大团的随机变量函数
• ${\prod }_C$代表对最大团的随机变量函数作累乘
• $Z$代表的是规范化因子，为了让 $P(Y)$满足一个概率，公式如下：
  $$Z=\sum _Y\prod _C{\psi }_C(Y_C)$$

五、条件随机场

设$X和Y$是随机变量，$P(Y|X)$是给定$X$的条件下$Y$的条件概率分布，若随机变量$Y$构成一个由无向图$G=(V,E)$表示的马尔科夫随机场，也就满足3个性质，如图：

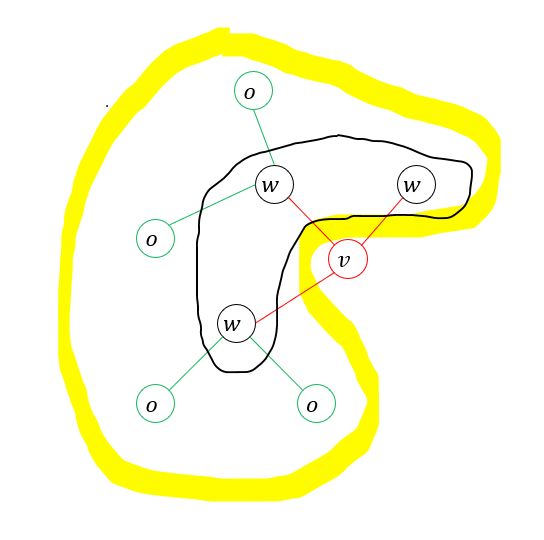
若以下公式
$$P(Y_v|X,Y_w,w\ne v)=P(Y_v|X,Y_w,w\approx v)$$

对任意的随机变量$v$成立，则称$P(Y|X)$为条件随机场。

• $X,Y_w,w\ne v$ 代表的就是给定$X$,给定除$v$随机变量以外的其他所有随机变量，图中黄线所画的
• $X,Y_w,w\approx v$ 代表的就是给定$X$，给定跟$v$随机变量直接相连的随机变量，图中黑线所画的

等式的意思就是，$v$的条件概率分布在以下两个条件中，随机变量的概率分布是一样的

• 给定$X$,给定除$v$以外的其他所有随机变量
• 给定$X$,给定跟$v$直接相连的随机变量

---

补充：
很显然，我们发现以上的公式用到了局部的马尔科夫性如下：$$P(Y_v,Y_o|Y_w)=P(Y_v|Y_w)\cdot P(Y_o|Y_w)$$上面公式中$v和o$条件独立，也就是两者没有边直接相连，看图也可以看出来，这样我们就能推出来：
$$P(Y_v|Y_w,Y_o)=P(Y_v|Y_w)$$
因为$v和o$条件独立，所以求$v$的概率去掉$o$条件不会产生任何影响。$Y_w,Y_o$条件并在一起就是不是$v$随机变量的情况下$v$的概率就等于只与$v$相连的随机变量的情况下$v$的概率。

---

六、线性条件随机场

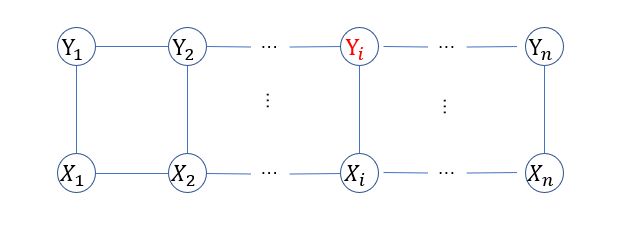
设 $X=(X_1,X_2,...,X_n)表示观测序列,Y=(Y_1,Y_2,...,Y_n)$表示状态序列，$XY$均为线性链表示的随机变量序列，若给定随机变量序列$X$的条件下，随机变量序列$Y$的条件概率分布$P(Y|X)$构成条件随机场，即满足马尔科夫性质：
$$P(Y_i|X,Y_1,Y_2,...,Y_n)=P(Y_i|X,Y_{i-1},Y_{i+1})$$则称$P(Y|X)$为线性条件随机场。

• $i$ 取值1到n
• 因为是线性的，所以跟$Y_i$相连的有$Y_{i-1}和Y_{i+1}$
• 给定$X和(Y_1,Y_2,...,Y_n)$的条件下$Y_i$的概率等于给定$X、Y_{i-1}、Y_{i+1}$的条件下的概率

一般研究的序列标注任务，不说明这个链是什么的情况下，默认指的就是线性条件随机场。

线性条件随机场的定义

以下是线性条件随机场的参数化形式，设$P(Y|X)$为线性条件随机场，则在随机变量$X$取$x$的条件下,随机变量$Y$取$y$的条件概率具有以下形式：
$$P(y|x)=\frac{1}{Z(x)}\cdot exp(\sum _{i,k}{\lambda }_k\cdot t_k(y_{i-1},y_i,x,i)+\sum _{i,l}{\mu }_l\cdot s_l(y_i,x,i))$$$$Z(x)=\sum _{y}exp(\sum _{i,k}{\lambda }_k\cdot t_k(y_{i-1},y_i,x,i)+\sum _{i,l}{\mu }_l\cdot s_l(y_i,x,i))$$

• $Z(x)$代表规范化因子，就是序列$y$的每一种可能性求和
• $t_k(y_{i-1},y_i,x,i)$代表边的特征函数（从$y_{i-1}到y_i$的边上的一个特征），称为状态转移，${\lambda }_k$代表参数
• ${\sum }_{i,k}$中$k$代表的是状态转移特征个数，$i$代表的是当前结点
• $s_l(y_i,x,i)$代表结点的特征函数（结点$y_i$上的一个特征），称为观测状态特征，${\mu }_l$代表参数
• ${\sum }_{i,l}$中$k$代表的是观测状态特征个数，$i$代表的是当前结点
• $exp(）$代表以e为底的函数
• 跟$y_i$组成最大团的是$y_{i-1}$,所以计算$y_{i-1},y_i$边上关系

例子

设有一标注问题，输入观测序列为$X=(X_1,X_2,X_3)$,输出标记序列为$Y=(Y_1,Y_2,Y_3)$,$Y_1,Y_2,Y_3$取值于y = { 1, 2},
假定特征函数的值都为1,即$t_1=t_2=...=t_5=1$，$s_1=s_2=s_3=s_4=1$

已知条件：

状态转移特征：

• $t_1(y_1=1,y_2=2,X,i=2)$ ${\lambda }_1=1$
• $t_1(y_2=1,y_3=2,X,i=3)$ ${\lambda }_1=1$
• $t_2(y_1=1,y_2=1,X,i=2)$ ${\lambda }_2=0.6$
• $t_3(y_2=2,y_3=1,X,i=3)$ ${\lambda }_3=1$
• $t_4(y_1=2,y_2=1,X,i=2)$ ${\lambda }_4=1$
• $t_5(y_2=2,y_3=2,X,i=3)$ ${\lambda }_5=0.2$

观测状态特征：

• $s_1(y_1=1,X,i=1)$ ${\mu }_1=1$
• $s_2(y_i=2,X,i)其中i取值\{1,2\}$ ${\mu }_2=0.5$
• $s_3(y_i=1,X,i)其中i取值\{2,3\}$ ${\mu }_3=0.8$
• $s_4(y_3=2,X,i=3)$ ${\mu }_4=0.5$

由已知条件，状态转移特征有5个，观测状态特征有4个，对给定的观测序列$X$，求标记序列为$y=(y_1,y_2,y_3)=(1,2,2)$的非规范化条件概率(也就是没有$Z(x)$这一项),$\propto$代表近似：

$$P(y|x)\propto exp(\sum _{k=1}^5{\lambda }_k\cdot \sum _{i=2}^3\cdot t_k(y_{i-1},y_i,x,i)+\sum _{l=1}^4{\mu }_l\cdot \sum _{i=1}^3\cdot s_l(y_i,x,i))$$
我们找到所有满足序列$(1,2,2)$的情况：

当$i=2,y_1=1,y_2=2,k=1时$: 1 · 1 = 1
当$i=3,y_2=2,y_3=2,k=5时$: 0.2 · 1 = 0.2

当$i=1,y_1=1,l=1时$: 1 · 1 = 1
当$i=2,y_2=2,l=2时$: 0.5 · 1 = 0.5
当$i=3,y_3=2,l=4时$: 0.5 · 1 = 0.5

所有情况加起来:1+0.2+1+0.5+0.5 = 3.2
$$P(y|x)\propto exp(3.2)$$

$(Y_1,Y_2,Y_3)$分别都有{1,2}两种可取值，所以总共有2·2·2=8种取值方式，将每种取值的情况$P(y|x)$加起来就是$Z(x)$,然后代入公式
$$P(y|x)=\frac{1}{Z(x)}\cdot exp(\sum _{i,k}{\lambda }_k\cdot t_k(y_{i-1},y_i,x,i)+\sum _{i,l}{\mu }_l\cdot s_l(y_i,x,i))$$中，便得到条件随机场的最终的结果。