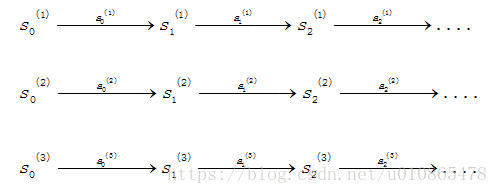统计概率模型-马尔科夫决策过程
统计概率模型
1、高斯判别分析
2、朴素贝叶斯
3、隐马尔可夫模型
4、最大熵马尔科夫模型
5,条件随机场
6,马尔科夫决策过程
六、马尔科夫决策过程
机器学习算法(有监督,无监督,弱监督)中,马尔科夫决策过程是弱监督中的一类叫增强学习。增加学习与传统的有监督和无监督不同的地方是,这些方法都是一次性决定最终结果的,而无法刻画一个决策过程,无法直接定义每一次决策的优劣,也就是说每一次的决策信息都是弱信息,所以某种程度上讲,强化学习也属于弱监督学习。从模型角度来看,也属于马尔科夫模型,其与隐马尔科夫模型有非常强的可比性。
下面是一个常用的马尔科夫模型的划分关系
| - | 不考虑动作 | 考虑动作 |
|---|---|---|
| 状态完全可见 | 马尔科夫链(MC) | 马尔科夫决策过程(MDP) |
| 状态不完全可见 | 隐马尔科夫模型(HMM) | 不完全可观察马尔科夫决策过程(POMDP) |
马尔科夫决策过程
马尔科夫决策过程由五元组组成 {S,A,Psa,γ,R} { S , A , P s a , γ , R }
S S :表示状态集合
A A :表示一组动作
Psa P s a :表示在某一状态 Si S i 下,采取动作 Ai A i ,转移到 Si+1 S i + 1 转态的概率,也就是说在确定的状态下采取相应的动作之后不能完全确定下一状态,而是以一定的概率确定下一状态。
γ γ :表示决策过程的一个阻尼系数,用户定义回报在决策过程中随时间打折扣,加快决策国产的收敛
R R :表示在该状态下的一个回报 R(s) R ( s ) ,有时由动作和状态共同决定回报该时刻的回报 R(a,s) R ( a , s ) 。
有了上面的定义之后,一个完整的马尔科夫决策过程状态转移图如下:
该过程表示从 S0 S 0 出发,有决策函数来选择相应的动作 a0 a 0 ,然后以概率 Pa,s P a , s 到达下一状态 Si∈S{Psa} S i ∈ S { P s a } ,这里的 Si S i 只是表示第 i i 时刻的状态,而 Si S i 的值属于状态集。
回报函数定义之后,整个决策过程的累积回报如下:
当回报函数与状态无关累积回报如下:
其中 γ γ 为折扣因子,随着决策不断进行,回报不断打折扣。
当定义不同决策函数时,我们会得到不同的回报,因此就定义了一个决策到回报的函数。在整个决策过程中,给定决策函数 a=π(s) a = π ( s ) —在 s s 状态下采取 π(s) π ( s ) 动作。因此,从状态 s=s0 s = s 0 出发,采用决策函数 a=π(s) a = π ( s ) ,有累积回报函数如下:
直接最大化累积回报函数不易,从递推角度来看,由贝尔曼方程有:
其中 R(s0)=V(s0−>s0) R ( s 0 ) = V ( s 0 − > s 0 ) 为立即回报, s1∈S s 1 ∈ S 表示由 s0 s 0 采取 πs0 π s 0 动作之后转移到下一个状态集中,具体到哪个状态的概率为 Ps0π(s0) P s 0 π ( s 0 ) 。其解释性可以理解为下象棋最终的累积回报为输赢,在第 s s 状态下的累积回报则是当前状态下的立即回报以及未来的回报。第一项为立即回报,第二项就是未来的回报。
有了上面的贝尔曼方程,我们的目标就是最大化任意状态下出发的累积回报函数 Vπ(s) V π ( s ) ,其中 a=π(s) a = π ( s ) 也是一个决策函数,但是在累积回报函数中它是我们需要优化的变量。目标函数如下:
由目标函数可以看出,最优回报和最优决策一一对应。最大化累积回报对应的决策函数 π π 就是最有决策,最有决策对应的累积回报也是最大累积回报,所以最有决策如下:
有了最优决策和最大累积回报,那么必定有下式:
也就是说最优决策下对应的累积回报一定不小于一般的决策下的累积回报。
值得注意是,最优决策是出于全局考虑的,是从所有状态下出发到得到的累积回报的加和最大,这就意味着决策函数不保证其中每一个状态出发根据决策函数得到的累积回报都是最大的。
最优决策
也许上面的目标函数还不清晰,如何求解最有决策,如何最大化累积回报
下面结合例子来介绍如何求解上面的目标函数。且说明累积回报函数本身就是一个过程的累积回报,回报函数 R R 才是每一步的回报。
下面再来看求解上述最优问题,其中 就是以s为初始状态沿着决策函数走到结束状态的累积回报。
值迭代
1将每一个初始状态为s的 V(s) V ( s ) 初始化为0,目标状态累积回报为1
2循环直到收敛{
对于每一个初始状态 s s ,对 V V 进行更新 V(s)=R(s)+γmaxa∈A∑s1∈SPs0π(s0)Vπ(s) V ( s ) = R ( s ) + γ max a ∈ A ∑ s 1 ∈ S P s 0 π ( s 0 ) V π ( s )
}
可以看出,更新第一次所有的 Vs:=R(s) V s := R ( s ) ,也就是说都只看眼下的立即回报,然后由于奖励状态和惩罚状态的分布不同,由靠近奖励状态和惩罚状态的状态决策逐渐导向到初始状态的决策,这也就是累积回报不断更新的原因(动力)。但是值得思考的还是最终会不会收敛到最优累积回报(暂时不作讨论)。
内循环迭代的的处理方法有两种:
1同步迭代:即在一次循环过程中,累积回报不更新,而是计算完所有的累积回报之后,再统一更新。
2异步迭代,即在一次循环过程中,每计算完一个初始状态下累积回报就立即更新,不需要等到所有的累积回报都计算出来之后再更新。
可以看出两种迭代方式造成不同的原因是第二项,因为立即更新之后,再计算下一个初始状态下的累积回报与暂时不更新得到的累积回报肯定不一样,拿第一次更新为例,同步更新第一次 V(s)=R(s) V ( s ) = R ( s ) ,而异步更新则第一次内循环中,除了第一次更新的s会出现 V(s)=R(s) V ( s ) = R ( s ) ,剩下的都有 V(s)≠R(s) V ( s ) ≠ R ( s ) ,值得肯定的是异步迭代的收敛速度肯定是快于同步迭代。
策略迭代
值迭代是使累积回报值最优为目标进行迭代,而策略迭代是借助累积回报最优即策略最优的等价性,进行策略迭代。
1随机指定一个策略 π:S→A π : S → A 。
2循环直到收敛{
a:令 V:=Vπ V := V π
b:对于每一个状态s,对 π(s) π ( s ) 做更新 πs:=argmaxa∈A∑s1∈SPsa(s1)V(s1) π s := a r g max a ∈ A ∑ s 1 ∈ S P s a ( s 1 ) V ( s 1 )
}
这里要说明的是a步是通过前面的贝尔曼方程,以解方程的形式求解出每一个状态下的累积回报:
在b步则是根据累积回报值,重新更新决策 π(s) π ( s ) 。
同样,收敛性也是值得探讨的,这里简单的思考一下,由于奖励状态和惩罚状态的分布,以及累积回报唯一确定决策函数,那么未达到最优决策,必然累积回报和决策函数处于不稳定的状态,而只有当到达最优决策时,才有
所以该过程就是在a步由决策函数确定累积回报,然后最大化累积回报来更新决策,如此反复,则有最优决策。值迭代和策略迭代比较:可以看出策略迭代涉及从决策函数到累积回报的解线性方程组的步骤,值迭代则是反复的,所以策略迭代更适合处理少量状态的情况,一般10000以内还是可以接受的。
MDP中的参数估计
回过头来再来看前面的马尔科夫决策过程的定义是一个五元组,一般情况下,五元组应该是我们更加特定的问题建立马尔科夫决策模型时该确定的,并在此基础上来求解最优决策。所以在求解最优决策之前,我们还需更加实际问题建立马尔科夫模型,建模过程就是确定五元组的过程,其中我们仅考虑状态转移概率 ,那么也就是一个参数估计过程。(其他参数一般都好确定,或设定)
假设,在时间过程中,我们有下面的状态转移路径:
其中 s(j)i s i ( j ) 表示 i i 步,第 j j 条转移路径对应的状态, a(j)i a i ( j ) 是 s(j)i s i ( j ) 状态下执行的动作,每一条转移路径中状态数都是有限的,在实际过程中,每一个状态转移路径都要进入终结状态。如果我们获得了很多上面的转移路径,那么我们就可以来估计参数 Psa P s a
分子是在 st s t 状态下采取 a a 动作都转移到 st+11 s t + 11 的次数,分母是在 s s 状态下采取 a a 动作的次数。为了避免 00 0 0 的情况,同样采用拉普拉斯平滑。也就是说当到达的状态是样本中为为到达过的状态,那么在该状态下的执行的动作达到下一状态的概率均分。上面的这种估计方法是从历史数据中进行统计的,同样该方法适合于在线更新。对于立即回报函数的估计,一般根据实际情况学习或者设定。
所以整个马尔科夫决策过程流程如下(以策略迭代为例):
1 随机初始化策略 π:S→A π : S → A 。
2循环直到收敛{
a在样本上统计该策略下每个状态转移的次数,来估计 Psa P s a 和 R R
b使用估计到参数来更新对应决策函数下的累积回报 V V
c根据更新的累积回报 V V 重新进行决策,即更新 π π
}
整个流程就是在策略迭代的基础上,同时进行了参数估计。