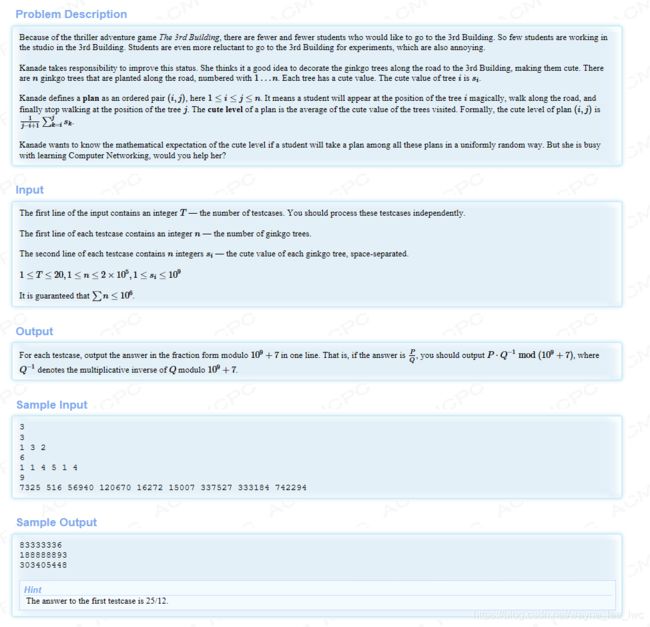
士兵过河2025B卷目录点击查看:华为OD机试2025B卷真题题库目录|机考题库+算法考点详解华为OD2025B卷200分题型题目描述一支N个士兵的军队正在趁夜色逃亡,途中遇到一条湍急的大河。敌军在T的时长后到达河面,没到过对岸的士兵都会被消灭。现在军队只找到了1只小船,这船最多能同时坐上2个士兵。当1个士兵划船过河,用时为a[i];0<=i
【论文笔记ing】Pointerformer: Deep Reinforced Multi-Pointer Transformer for the Traveling Salesman Problem
Booksort
online笔记论文论文阅读transformer深度学习
论文中使用一个PointerFormer模型编码器部分:可逆残差模型堆叠解码器部分:指针网络自回归对于一次任务而言,推理阶段:编码器部分:一次解码器部分:循环N次,直至任务结束在训练阶段,使用强化学习,对于一个N个节点的TSP实例,算法中会以不同的起点,跑N次,得到N个轨迹,以满足TSP的对称特性,表示这都是属于一个TSP问题的(真实)解然后会计算这样表示归一化奖励,得到一个advantage,然
【题解-Acwing】1057. 股票买卖 IV
X CODE
算法练习题解算法动态规划状态机模型
题目:1057.股票买卖IV题目描述给定一个长度为NNN的数组,数组中的第iii个数字表示一个给定股票在第iii天的价格。设计一个算法来计算你所能获取的最大利润,你最多可以完成kkk笔交易。注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。一次买入卖出合为一笔交易。输入格式第一行包含整数NNN和kkk,表示数组的长度以及你可以完成的最大交易笔数。第二行包含NNN个不超过10000
Redis 分布式锁实现与实践
佑瞻
数据库与知识图谱redis分布式数据库
在分布式系统架构中,多个独立进程对共享资源的并发访问控制是常见需求,分布式锁作为解决这一问题的关键技术,在缓存更新、任务调度、库存管理等场景中发挥着重要作用。本文将从基础原理出发,详细阐述基于Redis的分布式锁实现方案,包括单实例模式与Redlock算法,并探讨其在实际应用中的关键考量。分布式锁核心概念分布式锁是一种跨进程、跨机器的同步机制,用于保证多个分布式节点对共享资源的互斥访问。一个可靠的
布隆过滤器详解及使用:解决缓存穿透问题
豪宇刘
缓存哈希算法散列表
在现代应用开发中,缓存技术被广泛应用于提升系统性能和响应速度。然而,缓存系统也带来了一些新的挑战,如缓存穿透、缓存击穿和缓存雪崩等问题。一、什么是布隆过滤器?布隆过滤器是一种空间效率很高的概率型数据结构,用于判断一个元素是否在一个集合中。它的优点是高效且占用内存少,但有一定的误判率(即可能会错误地认为某个不在集合中的元素存在于集合中),不过它不会漏报(即如果一个元素确实不在集合中,布隆过滤器一定能
Unity Netcode自定义数据传输——结构体及其序列化
未来的中科院院士
unity游戏引擎
在UnityNetcode中,要实现自定义数据的网络传输,确实需要两个关键部分:✅两个必需组件:数据结构定义publicstructPlayerState:INetworkSerializable{publicintid;//字段1:玩家IDpublicboolisReady;//字段2:准备状态//...其他字段}作用:定义要传输的数据内容本质:声明"要传输什么"序列化方法实现publicvoi
使用工厂模式和策略模式实现布隆过滤器
小菜0-o
策略模式
使用工厂模式和策略模式实现布隆过滤器的大概流程如下:定义布隆过滤器接口:首先定义一个布隆过滤器接口,包括添加元素和判断元素是否存在两个基本操作。实现具体的布隆过滤器类:创建一个具体的布隆过滤器类,实现布隆过滤器接口中的方法。在这个类中,需要定义布隆过滗器的数据结构(比如位数组)、大小等属性。定义哈希策略接口:定义一个哈希策略接口,包含计算哈希值的方法。实现具体的哈希策略类:创建多个具体的哈希策略类
【机器学习-08】参数调优宝典:网格搜索与贝叶斯搜索等攻略
云天徽上
机器学习机器学习人工智能
博主简介:曾任某智慧城市类企业算法总监,目前在美国市场的物流公司从事高级算法工程师一职,深耕人工智能领域,精通python数据挖掘、可视化、机器学习等,发表过AI相关的专利并多次在AI类比赛中获奖。CSDN人工智能领域的优质创作者,提供AI相关的技术咨询、项目开发和个性化解决方案等服务,如有需要请站内私信或者联系任意文章底部的的VX名片(ID:xf982831907)博主粉丝群介绍:①群内初中生、
【2025B卷专题】华为OD机试2025B卷统一考试题库清单,时间紧张就刷这个
专栏导读本专栏收录于《华为OD机试(JAVA)真题(B卷+A卷+C卷+D卷+E卷)》。刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景,发现新题目,随时更新,全天CSDN在线答疑。2025年5月12日,华为官方已经将华为OD机试(A卷)切换为B卷。目前正在考的是B卷,按照华
【2025B卷专题】华为OD机试2025B卷统一考试题库清单,时间紧张就刷这个(Python/JS/C/C++)
哪 吒
搬砖工逆袭Java架构师华为odpythonjavascript华为OD机试2025B卷
专栏导读本专栏收录于《华为OD机试真题(Python/JS/C/C++)》。刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景,发现新题目,随时更新。2025年5月12日,华为官方已经将华为OD机试(A卷)切换为B卷。目前正在考的是B卷,按照华为OD往常的操作,B卷题目是由往
【全网首发】华为OD机试 2025B卷 机考真题库清单(全真题库)含考点说明
哪 吒
搬砖工逆袭Java架构师华为odjava2025B卷华为OD机试
专栏导读本专栏收录于《华为OD机试(JAVA)真题(E卷+D卷+A卷+B卷+C卷)》。刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景,发现新题目,随时更新,全天CSDN在线答疑。2025年5月12日,华为官方已经将华为OD机试(A卷)切换为B卷。目前正在考的是B卷,按照华
【2025B卷首发】华为OD机试真题+全流程解析+备考攻略+经验分享+Java最佳实现
专栏导读本专栏收录于《华为OD机试(JAVA)真题(E卷+D卷+A卷+B卷+C卷)》。刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景,发现新题目,随时更新,全天CSDN在线答疑。2025年5月12日,华为官方已经将华为OD机试(A卷)切换为B卷。目前正在考的是B卷,按照华
PyTorch 在 Python 自然语言处理中的运用
Python编程之道
Python编程之道pythonpytorch自然语言处理ai
PyTorch在Python自然语言处理中的运用关键词:PyTorch,Python,自然语言处理,深度学习,文本分类,情感分析摘要:本文全面探讨了PyTorch在Python自然语言处理(NLP)领域的运用。首先介绍了相关背景知识,包括目的范围、预期读者等内容。接着详细阐述了核心概念,如词嵌入、循环神经网络等,并给出了相应的原理示意图和流程图。深入讲解了核心算法原理,结合Python代码进行详细
后端领域的自然语言处理技术应用
大厂资深架构师
SpringBoot开发实战自然语言处理easyui人工智能ai
后端领域的自然语言处理技术应用关键词:后端领域、自然语言处理、技术应用、算法原理、实际案例摘要:本文聚焦于后端领域中自然语言处理技术的应用。首先介绍了相关背景,包括目的范围、预期读者等。接着阐述核心概念与联系,通过文本示意图和Mermaid流程图展示其原理和架构。详细讲解了核心算法原理并给出Python源代码示例,同时介绍了数学模型和公式。通过项目实战,展示代码实际案例并进行详细解释。分析了自然语
redis做同步或异步队列
瞧着不像好人呐
redisredisjava数据库
redis实现队列主要是使用数据结构中的list,相当于Java中的ArrayList因为它是按照塞入顺序排序的结构,我们就可以按照左边塞入,右边取出的方式来实现先入先出的队列需求。publicvoidrpush(Stringkey,Stringvalue){Jedisjedis=null;try{jedis=jedisPool.getResource();jedis.rpush(key,valu
Hutool TreeUtil快速构建树形数据结构
yifanghub
工具类java
在管理菜单、部门结构等场景时,我们经常需要将数据库中的层级数据转换为树形结构。本文将通过Hutool的TreeUtil工具类,实现零递归快速构建树形结构。一、环境准备JDK1.8+SpringBoot2.xHutool5.8.16MySQL8.0二、数据准备--创建部门表CREATETABLE`sys_dept`(`id`intNOTNULLAUTO_INCREMENT,`dept_name`va
Camera相机人脸识别系列专题分析之十六:人脸特征检测FFD算法之libcvface_api.so数据结构详细注释解析
一起搞IT吧
数码相机算法数据结构人工智能android图像处理计算机视觉
【关注我,后续持续新增专题博文,谢谢!!!】上一篇我们讲了:这一篇我们开始讲:Camera相机人脸识别系列专题分析之十六:人脸特征检测FFD算法之libcvface_api.so数据结构详细注释解析目录一、libcvface_api.so数据结构详细注释解析一、libcvface_api.so数据结构详细注释解析///@brief人脸信息结构体typedefstructcv_face_t{cv_r
四、Actor-Critic Methods
沈夢昂志
DRL深度强化学习python深度学习
由于在看DRL论文中,很多公式都很难理解。因此最近在学习DRL的基本内容。再此说明,非常推荐B站“王树森老师的DRL强化学习”本文的图表及内容,都是基于王老师课程的后自行理解整理出的内容。目录A.书接上回1、Reinforce算法B.State-ValueFunctionC.PolicyNetWork(Actor)D.ActionValueNetwork(Critic)E.TraintheNeur
Char Studio 使用入门:高效构建企业级对话系统的实战指南
charles666666
人工智能产品经理语言模型自然语言处理架构
数字化浪潮推动下,企业与用户的交互模式正经历深刻变革,对话系统作为核心交互手段,其重要性日益凸显。然而,众多企业在构建对话系统时,却深陷诸多困境,难以自拔。一、开篇痛点场景:企业对话系统开发的典型困境企业在自行开发对话系统时,往往面临预算超支、周期漫长以及维护成本居高不下等问题。开发团队需要投入大量时间和精力进行底层技术架构的搭建,例如自然语言处理算法的研究、对话逻辑的设计等,这不仅消耗了大量的人
Pandas 学习(数学建模篇)
停走的风
数学建模pandas学习
今天学习数学建模2023年C篇(228)优秀论文2023高教社杯全国大学生数学建模竞赛C题论文展示(C228)-2023C题论文-中国大学生在线一.pd.DataFramepd.DataFrame()是pandas库中用于创建二维表格数据结构(DataFrame)的核心函数。它的作用是将各种格式的数据(如字典、列表、Series等)转换为带有行索引和列标签的表格形式,便于数据处理和分析.impor
AI驱动的个人工作革命:基于DeepSeek构建全场景智能工作助理(含源代码+多应用场景)
AI_DL_CODE
DeepSeek深度应用人工智能DeepSeek个人智能助理LangChain任务自动化知识管理大模型应用
摘要:本文详细阐述基于DeepSeek大模型构建个人工作助理的完整技术方案,通过LangChain实现任务分解、知识检索与工具调用的智能协同。方案融合向量数据库、多模态交互与个性化学习算法,构建涵盖邮件处理、会议管理、文档生成等15大核心工作场景的自动化系统。文中提供可运行代码、完整部署指南及效能测试数据,实现邮件处理效率提升13倍、会议纪要生成时间缩短100%、任务安排错误率降低83%的显著优化
python中的pydantic是什么?
John Song
Pythonpython前端开发语言pydantic
Pydantic是Python中一个用于数据验证和设置管理的库,主要通过Python类型注解(TypeHints)来定义数据结构,并自动验证输入数据的合法性。它广泛应用于API开发(如FastAPI)、配置管理、数据序列化等场景。核心功能数据验证自动检查输入数据是否符合类型和约束条件(如字符串长度、数字范围等)。类型转换将原始数据(如JSON、字典)转换为Python类型(如datetime、En
异物检测的计算机视觉算法技术路线
思绪漂移
计算机视觉算法人工智能
异物检测的计算机视觉算法技术路线在现代智能监测系统中,异物检测有着其必要性和运维重要性,通过计算机视觉算法,可以实时识别各种异常物体,为设备安全运行提供有力保障。本文将介绍异物检测的主要技术路线。一、分类识别适应场景分类识别技术主要适用于已知目标类别的异物检测场景。在运维环境中,这类场景包括:固定区域内的障碍物监测(如轨道区域的石块、工具、动物等)关键部件的异物附着检测(如固定装置上的杂物)安全通
PageRank:互联网的马尔可夫链平衡态
大千AI助手
人工智能Python#OTHER人工智能机器学习条件概率贝叶斯PageRank马尔科夫链MC
本文由「大千AI助手」原创发布,专注用真话讲AI,回归技术本质。拒绝神话或妖魔化。搜索「大千AI助手」关注我,一起撕掉过度包装,学习真实的AI技术!PageRank算法本质上是一个在网页图上定义的离散时间马尔可夫链(DTMC),其核心思想是将网页间的链接关系转化为状态转移概率。以下是详细分析:一、马尔可夫链的核心要素在PageRank中的体现马尔可夫链要素PageRank对应数学描述状态空间网页集
MCMC:高维概率采样的“随机游走”艺术
大千AI助手
人工智能Python#OTHER人工智能数据挖掘机器学习算法MCMC马尔科夫概率论
MCMC(马尔可夫链蒙特卡洛)是一种从复杂概率分布中高效采样的核心算法,它解决了传统采样方法在高维空间中的“维度灾难”问题。以下是其技术本质、关键算法及实践的深度解析:本文由「大千AI助手」原创发布,专注用真话讲AI,回归技术本质。拒绝神话或妖魔化。搜索「大千AI助手」关注我,一起撕掉过度包装,学习真实的AI技术!一、MCMC要解决的核心问题目标:从目标分布(π(x)\pi(\mathbf{x})
LeetCode 刷题:数据结构与算法的实战经验分享
LeetCode刷题:数据结构与算法的实战经验分享关键词:LeetCode、数据结构、算法、刷题经验、实战摘要:本文将围绕LeetCode刷题展开,深入探讨数据结构与算法在实际刷题过程中的应用。通过分享实战经验,帮助读者更好地理解和掌握数据结构与算法知识,提升解题能力。文章将从背景介绍入手,阐述刷题的目的和意义,接着详细解释核心概念,分析它们之间的关系,然后介绍核心算法原理和具体操作步骤,结合数学
高压电缆护层电流监测系统的技术实现
李子圆圆
人工智能
目录文章目录概要高精度电流监测的技术实现多级预警机制的构建逻辑极端环境下的稳定运行技术远程运维的技术支撑概要高压电缆护层作为电力传输的关键防护结构,其接地电流的异常变化是判断设备状态的重要指标。TLKS-PLGD高压电缆护层电流监测系统通过传感器技术与智能算法的结合,构建了一套完整的电缆安全监测方案。高精度电流监测的技术实现高精度电流监测的技术实现护层电流监测的核心在于数据采集的精准性。该系统采用
构建安全密码存储策略:核心原则与最佳实践
weixin_47233946
信息安全安全
密码是用户身份认证的第一道防线,其存储安全性直接关系到用户隐私和企业信誉。近年来频发的数据泄露事件揭示了密码管理的关键性。本文将深入探讨从加密算法到系统性防护的完整密码存储方案,帮助开发者构建企业级安全防御体系。一、密码存储基本准则绝对禁止明文存储:即使采用数据库加密措施,直接存储用户原始密码仍存在不可逆泄露风险。运维人员权限滥用或备份文件泄露都可能成为突破口。加密≠安全:AES等对称加密存在密钥
数据结构实验解析(C++版)——实验一 复杂度分析
拯救三金
数据结构c++算法
目录一、实验例题例题1例题2二、实验原理与背景知识1、实验原理2、背景知识三、解题思路与算法1、解题思路2、算法四、代码实现例题1代码例题2代码五、实验结果分析与总结1、实验结果分析2、该实验与数据结构的联系一、实验例题例题1时间空间限制时间限制:1SEC空间限制:128MB问题描述分析以下代码:for(i=1;iusingnamespacestd;intmain(){longlongn;//输入
Spring Data Neo4j 与后端人工智能算法的数据交互
AI大模型应用实战
springneo4j人工智能ai
SpringDataNeo4j与后端人工智能算法的数据交互关键词:SpringDataNeo4j、图数据库、人工智能算法、数据交互、知识图谱、图神经网络、数据集成摘要:本文深入探讨了如何利用SpringDataNeo4j框架实现后端人工智能算法与图数据库的高效数据交互。文章首先介绍了图数据库和人工智能算法的基本概念,然后详细解析了SpringDataNeo4j的核心架构和原理。接着,通过实际代码示
redis学习笔记——不仅仅是存取数据
Everyday都不同
returnSourceexpire/delincr/lpush数据库分区redis
最近项目中用到比较多redis,感觉之前对它一直局限于get/set数据的层面。其实作为一个强大的NoSql数据库产品,如果好好利用它,会带来很多意想不到的效果。(因为我搞java,所以就从jedis的角度来补充一点东西吧。PS:不一定全,只是个人理解,不喜勿喷)
1、关于JedisPool.returnSource(Jedis jeids)
这个方法是从red
SQL性能优化-持续更新中。。。。。。
atongyeye
oraclesql
1 通过ROWID访问表--索引
你可以采用基于ROWID的访问方式情况,提高访问表的效率, , ROWID包含了表中记录的物理位置信息..ORACLE采用索引(INDEX)实现了数据和存放数据的物理位置(ROWID)之间的联系. 通常索引提供了快速访问ROWID的方法,因此那些基于索引列的查询就可以得到性能上的提高.
2 共享SQL语句--相同的sql放入缓存
3 选择最有效率的表
[JAVA语言]JAVA虚拟机对底层硬件的操控还不完善
comsci
JAVA虚拟机
如果我们用汇编语言编写一个直接读写CPU寄存器的代码段,然后利用这个代码段去控制被操作系统屏蔽的硬件资源,这对于JVM虚拟机显然是不合法的,对操作系统来讲,这样也是不合法的,但是如果是一个工程项目的确需要这样做,合同已经签了,我们又不能够这样做,怎么办呢? 那么一个精通汇编语言的那种X客,是否在这个时候就会发生某种至关重要的作用呢?
&n
lvs- real
男人50
LVS
#!/bin/bash
#
# Script to start LVS DR real server.
# description: LVS DR real server
#
#. /etc/rc.d/init.d/functions
VIP=10.10.6.252
host='/bin/hostname'
case "$1" in
sta
生成公钥和私钥
oloz
DSA安全加密
package com.msserver.core.util;
import java.security.KeyPair;
import java.security.PrivateKey;
import java.security.PublicKey;
import java.security.SecureRandom;
public class SecurityUtil {
UIView 中加入的cocos2d,背景透明
374016526
cocos2dglClearColor
要点是首先pixelFormat:kEAGLColorFormatRGBA8,必须有alpha层才能透明。然后view设置为透明glView.opaque = NO;[director setOpenGLView:glView];[self.viewController.view setBackgroundColor:[UIColor clearColor]];[self.viewControll
mysql常用命令
香水浓
mysql
连接数据库
mysql -u troy -ptroy
备份表
mysqldump -u troy -ptroy mm_database mm_user_tbl > user.sql
恢复表(与恢复数据库命令相同)
mysql -u troy -ptroy mm_database < user.sql
备份数据库
mysqldump -u troy -ptroy
我的架构经验系列文章 - 后端架构 - 系统层面
agevs
JavaScriptjquerycsshtml5
系统层面:
高可用性
所谓高可用性也就是通过避免单独故障加上快速故障转移实现一旦某台物理服务器出现故障能实现故障快速恢复。一般来说,可以采用两种方式,如果可以做业务可以做负载均衡则通过负载均衡实现集群,然后针对每一台服务器进行监控,一旦发生故障则从集群中移除;如果业务只能有单点入口那么可以通过实现Standby机加上虚拟IP机制,实现Active机在出现故障之后虚拟IP转移到Standby的快速
利用ant进行远程tomcat部署
aijuans
tomcat
在javaEE项目中,需要将工程部署到远程服务器上,如果部署的频率比较高,手动部署的方式就比较麻烦,可以利用Ant工具实现快捷的部署。这篇博文详细介绍了ant配置的步骤(http://www.cnblogs.com/GloriousOnion/archive/2012/12/18/2822817.html),但是在tomcat7以上不适用,需要修改配置,具体如下:
1.配置tomcat的用户角色
获取复利总收入
baalwolf
获取
public static void main(String args[]){
int money=200;
int year=1;
double rate=0.1;
&
eclipse.ini解释
BigBird2012
eclipse
大多数java开发者使用的都是eclipse,今天感兴趣去eclipse官网搜了一下eclipse.ini的配置,供大家参考,我会把关键的部分给大家用中文解释一下。还是推荐有问题不会直接搜谷歌,看官方文档,这样我们会知道问题的真面目是什么,对问题也有一个全面清晰的认识。
Overview
1、Eclipse.ini的作用
Eclipse startup is controlled by th
AngularJS实现分页功能
bijian1013
JavaScriptAngularJS分页
对于大多数web应用来说显示项目列表是一种很常见的任务。通常情况下,我们的数据会比较多,无法很好地显示在单个页面中。在这种情况下,我们需要把数据以页的方式来展示,同时带有转到上一页和下一页的功能。既然在整个应用中这是一种很常见的需求,那么把这一功能抽象成一个通用的、可复用的分页(Paginator)服务是很有意义的。
&nbs
[Maven学习笔记三]Maven archetype
bit1129
ArcheType
archetype的英文意思是原型,Maven archetype表示创建Maven模块的模版,比如创建web项目,创建Spring项目等等.
mvn archetype提供了一种命令行交互式创建Maven项目或者模块的方式,
mvn archetype
1.在LearnMaven-ch03目录下,执行命令mvn archetype:gener
【Java命令三】jps
bit1129
Java命令
jps很简单,用于显示当前运行的Java进程,也可以连接到远程服务器去查看
[hadoop@hadoop bin]$ jps -help
usage: jps [-help]
jps [-q] [-mlvV] [<hostid>]
Definitions:
<hostid>: <hostname>[:
ZABBIX2.2 2.4 等各版本之间的兼容性
ronin47
zabbix更新很快,从2009年到现在已经更新多个版本,为了使用更多zabbix的新特性,随之而来的便是升级版本,zabbix版本兼容性是必须优先考虑的一点 客户端AGENT兼容
zabbix1.x到zabbix2.x的所有agent都兼容zabbix server2.4:如果你升级zabbix server,客户端是可以不做任何改变,除非你想使用agent的一些新特性。 Zabbix代理(p
unity 3d还是cocos2dx哪个适合游戏?
brotherlamp
unity自学unity教程unity视频unity资料unity
unity 3d还是cocos2dx哪个适合游戏?
问:unity 3d还是cocos2dx哪个适合游戏?
答:首先目前来看unity视频教程因为是3d引擎,目前对2d支持并不完善,unity 3d 目前做2d普遍两种思路,一种是正交相机,3d画面2d视角,另一种是通过一些插件,动态创建mesh来绘制图形单元目前用的较多的是2d toolkit,ex2d,smooth moves,sm2,
百度笔试题:一个已经排序好的很大的数组,现在给它划分成m段,每段长度不定,段长最长为k,然后段内打乱顺序,请设计一个算法对其进行重新排序
bylijinnan
java算法面试百度招聘
import java.util.Arrays;
/**
* 最早是在陈利人老师的微博看到这道题:
* #面试题#An array with n elements which is K most sorted,就是每个element的初始位置和它最终的排序后的位置的距离不超过常数K
* 设计一个排序算法。It should be faster than O(n*lgn)。
获取checkbox复选框的值
chiangfai
checkbox
<title>CheckBox</title>
<script type = "text/javascript">
doGetVal: function doGetVal()
{
//var fruitName = document.getElementById("apple").value;//根据
MySQLdb用户指南
chenchao051
mysqldb
原网页被墙,放这里备用。 MySQLdb User's Guide
Contents
Introduction
Installation
_mysql
MySQL C API translation
MySQL C API function mapping
Some _mysql examples
MySQLdb
HIVE 窗口及分析函数
daizj
hive窗口函数分析函数
窗口函数应用场景:
(1)用于分区排序
(2)动态Group By
(3)Top N
(4)累计计算
(5)层次查询
一、分析函数
用于等级、百分点、n分片等。
函数 说明
RANK() &nbs
PHP ZipArchive 实现压缩解压Zip文件
dcj3sjt126com
PHPzip
PHP ZipArchive 是PHP自带的扩展类,可以轻松实现ZIP文件的压缩和解压,使用前首先要确保PHP ZIP 扩展已经开启,具体开启方法就不说了,不同的平台开启PHP扩增的方法网上都有,如有疑问欢迎交流。这里整理一下常用的示例供参考。
一、解压缩zip文件 01 02 03 04 05 06 07 08 09 10 11
精彩英语贺词
dcj3sjt126com
英语
I'm always here
我会一直在这里支持你
&nb
基于Java注解的Spring的IoC功能
e200702084
javaspringbeanIOCOffice
java模拟post请求
geeksun
java
一般API接收客户端(比如网页、APP或其他应用服务)的请求,但在测试时需要模拟来自外界的请求,经探索,使用HttpComponentshttpClient可模拟Post提交请求。 此处用HttpComponents的httpclient来完成使命。
import org.apache.http.HttpEntity ;
import org.apache.http.HttpRespon
Swift语法之 ---- ?和!区别
hongtoushizi
?swift!
转载自: http://blog.sina.com.cn/s/blog_71715bf80102ux3v.html
Swift语言使用var定义变量,但和别的语言不同,Swift里不会自动给变量赋初始值,也就是说变量不会有默认值,所以要求使用变量之前必须要对其初始化。如果在使用变量之前不进行初始化就会报错:
var stringValue : String
//
centos7安装jdk1.7
jisonami
jdkcentos
安装JDK1.7
步骤1、解压tar包在当前目录
[root@localhost usr]#tar -xzvf jdk-7u75-linux-x64.tar.gz
步骤2:配置环境变量
在etc/profile文件下添加
export JAVA_HOME=/usr/java/jdk1.7.0_75
export CLASSPATH=/usr/java/jdk1.7.0_75/lib
数据源架构模式之数据映射器
home198979
PHP架构数据映射器datamapper
前面分别介绍了数据源架构模式之表数据入口、数据源架构模式之行和数据入口数据源架构模式之活动记录,相较于这三种数据源架构模式,数据映射器显得更加“高大上”。
一、概念
数据映射器(Data Mapper):在保持对象和数据库(以及映射器本身)彼此独立的情况下,在二者之间移动数据的一个映射器层。概念永远都是抽象的,简单的说,数据映射器就是一个负责将数据映射到对象的类数据。
&nb
在Python中使用MYSQL
pda158
mysqlpython
缘由 近期在折腾一个小东西须要抓取网上的页面。然后进行解析。将结果放到
数据库中。 了解到
Python在这方面有优势,便选用之。 由于我有台
server上面安装有
mysql,自然使用之。在进行数据库的这个操作过程中遇到了不少问题,这里
记录一下,大家共勉。
python中mysql的调用
百度之后能够通过MySQLdb进行数据库操作。
单例模式
hxl1988_0311
java单例设计模式单件
package com.sosop.designpattern.singleton;
/*
* 单件模式:保证一个类必须只有一个实例,并提供全局的访问点
*
* 所以单例模式必须有私有的构造器,没有私有构造器根本不用谈单件
*
* 必须考虑到并发情况下创建了多个实例对象
* */
/**
* 虽然有锁,但是只在第一次创建对象的时候加锁,并发时不会存在效率
27种迹象显示你应该辞掉程序员的工作
vipshichg
工作
1、你仍然在等待老板在2010年答应的要提拔你的暗示。 2、你的上级近10年没有开发过任何代码。 3、老板假装懂你说的这些技术,但实际上他完全不知道你在说什么。 4、你干完的项目6个月后才部署到现场服务器上。 5、时不时的,老板在检查你刚刚完成的工作时,要求按新想法重新开发。 6、而最终这个软件只有12个用户。 7、时间全浪费在办公室政治中,而不是用在开发好的软件上。 8、部署前5分钟才开始测试。