机器学习个人笔记——（二）Logistic回归

一、Logistic回归概念

1. 主要思想

回归 : 用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合过程就称作回归。
逻辑回归: 是一种适用于二分类（非0即1）的分类算法

根据现有数据对分类边界线建立回归公式，以此进行分类。
目标：找到最佳拟合参数集
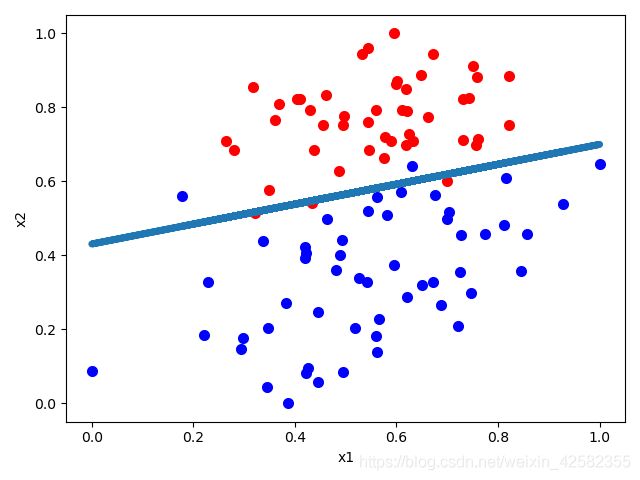
例如：下图所示，在一个平面中存在2个类别的数据，红色为：1，蓝色为0
此时画一条直线，平面上的点将被为两个部分，而我们所要求的就是这一条直线方程
假设这条直线方程为w0+w1*x1+w2*x2=0,而平面中的点是已知的，如：(x1, x2)=(1.0 , 0.6)，带入该方程中，得w0+w1*1.0+w2*0.6=z，若z>0，则在直线的上方，若z<0，类别1，则在直线的下方，类别0
问题即为：求一个最佳的的w0,w1,w2，使分类器尽可能地准确

数据处理过程中，通常会对原数据加入一个特征值1，原数据(x1,x2)=>(1,x1,x2)=(1, 1.0 ,0.6)
此时点向量为$$\begin{array}{rl}{\mathbf{x}}^{\mathbf{T}}& =\left[\begin{array}{ccc}{x}_0& x_1& x_2\end{array}\right]\\ & =\left[\begin{array}{ccc}1.0& 1.0& 0.6\end{array}\right]\end{array}$$

参数w0,w1,w2为
$$\begin{array}{rl}{\mathbf{w}}^{\mathbf{T}}& =\left[\begin{array}{ccc}{w}_0& w_1& w_2\end{array}\right]\end{array}$$

此时方程为
$$\begin{array}{rl}z& =w_0\ast 1.0+w_1\ast x_1+w_2\ast x_2\\ & =w_0\ast 1.0+w_1\ast 1.0+w_2\ast 0.6\\ & ={\mathbf{w}}^{\mathbf{T}}\mathbf{x}(向量相乘)\end{array}$$

2. 一般：

存在一个点(x1,x2,…xn), n为特征值的个数，对应的向量为
$$\begin{array}{rl}{\mathbf{x}}^{\mathbf{T}}& =\left[\begin{array}{ccccc}{x}_0& x_1& x_2& ...& x_n\end{array}\right]\\ & =\left[\begin{array}{ccccc}1& x_1& x_2& ...& x_n\end{array}\right]\end{array}$$
参数为:
$$\begin{array}{rl}{\mathbf{w}}^{\mathbf{T}}& =\left[\begin{array}{ccccc}{w}_0& w_1& w_2& ...& w_n\end{array}\right]\end{array}$$
因此：
$$\begin{array}{rl}z& =w_0\ast 1+w_1\ast x_1+w_2\ast x_2+...+w_n\ast x_n\\ & ={\mathbf{w}}^{\mathbf{T}}\mathbf{x}\end{array}$$

二、原理

1. Sigmoid 函数

Sigmoid 函数具体公式如下所示:
$$h(x)=\frac{1}{1+e^{-x}}$$
函数图像如图所示：

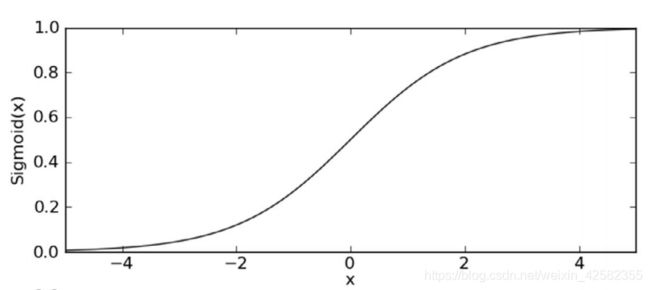
当x>0时，1>Sigmoid(x)>0.5
当x<0时，0
当x=0时，Sigmoid(x)=0.5

因为：
$\begin{array}{rl}z& =w_0\ast 1+w_1\ast x_1+w_2\ast x_2+...+w_n\ast x_n\\ & ={\mathbf{w}}^{\mathbf{T}}\mathbf{x}\end{array}$

将z代入Sigmoid函数中，进而得到一个范围在0~1 之间的数值。
$$h({\mathbf{w}}^{\mathbf{T}}\mathbf{x})=\frac{1}{1+e^{-{\mathbf{w}}^{\mathbf{T}}\mathbf{x}}}$$
大于0.5的数据被分入1 类，小于0.5即被归入0 类。

对Sigmoid函数求导，将在后面的推导中用到:
$$\begin{array}{rl}{h}^{{}^{\prime }}(x)& =\frac{d\frac{1}{1+e^{-x}}}{dx}\\ & =h(x)(1-h(x))\end{array}$$

2.构建似然函数

通过sigmoid函数 ，输出的值 p=$h({\mathbf{w}}^{\mathbf{T}}\mathbf{x})$
p的值表示结果为1的概率，1-p则表示结果为0的概率**
在一个数据集中(m表示样本数，n表示特征值个数)：
$\mathbf{x}=\left[\begin{array}{cccc}{x}_{10}& x_{20}& ...& x_{m0}\\ x_{11}& x_{21}& ...& x_{m1}\\ ...& & & \\ x_{1n}& x_{2n}& ...& x_{mn}\end{array}\right]$，则任意一个输入向量${\mathbf{x}}_{\mathbf{i}}=\left[\begin{array}{c}{x}_{i0}\\ x_{i1}\\ ...\\ x_{in}\end{array}\right]$
分类结果为类别1和类别0的概率分别为
$$\begin{array}{rl}{P}_i(y& =1|{\mathbf{x}}_{\mathbf{i}})=h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})(当该类别标签y=1时)\\ P_i(y& =0|{\mathbf{x}}_{\mathbf{i}})=1-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})(当该类别标签y=0时)\end{array}$$

对以上式子进行合并，得到
$$\begin{array}{r}{P}_i(y_i|{\mathbf{x}}_{\mathbf{i}})=(h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}){)}^{y_i}\ast (1-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}){)}^{(1-y_i)}\end{array}$$

构建似然函数：若训练样本相互独立，则似然函数为：
$$\begin{array}{rl}L(\mathbf{w})& =\prod _{i=1}^m{P}_i(y_i|{\mathbf{x}}_{\mathbf{i}})\\ & =\prod _{i=1}^m(h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}){)}^{y_i}\ast (1-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}){)}^{(1-y_i)}\end{array}$$

对似然函数进行一个转换，两边取log，将乘法运算转换为加法运算：
$$\begin{array}{rl}l{n}_{}L(\mathbf{w})& =\sum _{i=1}^m{y}_i{\ln }_{}h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})+(1-y_i)l{n}_{}(1-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))\\ & =l(\mathbf{w})\end{array}$$

似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性，可以理解为条件概率的逆反
以盒子中抓黑白球为例：
比如个一盒子中只有黑色和白色两种球，但不知道他们的数量是多少
现在从中抓10次(每次都放回)，得到了3次黑球，7次白球。
假设取到黑球的概率为P，则取到白球的概率为1-P
则 构建似然函数为
$L(P)=P^3\ast (1-P{)}^7$
此时，若存在一个参数值P, 即抓到黑球的概率，使得它的函数值L(P)达到最大的话，那么这个值P就是最为合理的参数值。
一般对L(P)进行求导，令导数为0，求得P所取的值

同理在逻辑回归中，也是二分类问题，当存在w使得L(w)取最大值时，那么此时的w即为合适的值，在当前问题中，$w=[w_0,w_1,w_2,...,w_n]$是一个n+1维的向量，即参数值

3.梯度上升

似然函数为：
$$\begin{array}{rl}l(\mathbf{w})& =\sum _{i=1}^m{y}_i{\ln }_{}h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})+(1-y_i)l{n}_{}(1-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))\end{array}$$
$l(\mathbf{w})$求最大值，使用梯度上升。

梯度：
一般来说，梯度可以定义为一个函数的全部偏导数构成的向量
指向函数值增长最快的方向

梯度上升：沿着增长最快的方向，移动$\alpha$ 的步长，迭代公式如下
$$w=w+\alpha \nabla f$$

即求$l(\mathbf{w})$的梯度, 需分别对对$w_i$求偏导

$$\nabla f=\left[\begin{array}{c}\frac{\partial \mathrm{l}(\mathbf{w})}{\partial {\mathrm{w}}_0}\\ \frac{\partial \mathrm{l}(\mathbf{w})}{\partial {\mathrm{w}}_1}\\ \frac{\partial \mathrm{l}(\mathbf{w})}{\partial {\mathrm{w}}_2}\\ ...\\ \frac{\partial \mathrm{l}(\mathbf{w})}{\partial {\mathrm{w}}_n}\end{array}\right]$$

对以上公式进行拆分，拿出一个来看
$\begin{array}{rl}\frac{\partial l(\mathbf{w})}{\partial w_0}& =\sum _{i=1}^m\frac{\partial \mathrm{h}({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})}{\partial {\mathrm{w}}_0}(\frac{y_i}{h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})}+\frac{1-y_i}{1-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})})\end{array}$

其中

$$\begin{array}{rl}& \because h^{{}^{\prime }}(x)=\frac{\mathrm{d}h(x)}{\mathrm{d}x}=h(x)(1-h(x))\\ & \\ & \therefore \frac{\partial \mathrm{h}({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})}{\partial {\mathrm{w}}_0}=h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})(1-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))\ast \frac{\partial ({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})}{\partial {\mathrm{w}}_0}\\ & =...\ast \frac{\partial (w_0{x}_0+w_1{x}_1+...+w_n{x}_n)}{\partial {\mathrm{w}}_0}\\ & =...\ast x_0\\ & =h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})(1-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))\ast x_0\\ & \\ & ....以此类推\\ & \therefore \frac{\partial \mathrm{h}({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})}{\partial {\mathrm{w}}_j}=h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})(1-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))\ast x_j(x_j=第j个特征值)\end{array}$$

代入原方程中得

$$\begin{array}{rl}\frac{\partial \mathrm{l}(\mathbf{w})}{\partial {\mathrm{w}}_0}& =\sum _{i=1}^m(h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})(1-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))\ast x_0)(\frac{y_i}{h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})}+\frac{1-y_i}{1-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}})})\\ 整理得& \\ & =\sum _{i=1}^m(y_i-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))x_{i0}\end{array}$$
所以：
$$\begin{array}{rl}\frac{\partial \mathrm{l}(\mathbf{w})}{\partial {\mathrm{w}}_j}& =\sum _{i=1}^m(y_i-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))x_{ij}(x_{ij}=第i个样本的第j个特征值)\end{array}$$

梯度可以表示为：
$$\nabla f=\frac{1}{m}\left[\begin{array}{c}{\sum }_{i=1}^m(y_i-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))x_{i0}\\ {\sum }_{i=1}^m(y_i-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))x_{i1}\\ {\sum }_{i=1}^m(y_i-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))x_{i2}\\ ......\\ {\sum }_{i=1}^m(y_i-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))x_{in}\end{array}\right]$$

梯度上升算法的迭代过程：$\alpha$ 为步长
$$\begin{array}{rl}\mathbf{w}& =\mathbf{w}+\alpha \nabla f\\ & \\ & =\left[\begin{array}{c}{w}_0\\ w_1\\ w_2\\ ...\\ w_n\end{array}\right]+\alpha \frac{1}{m}\left[\begin{array}{c}{\sum }_{i=1}^m(y_i-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))x_{i0}\\ {\sum }_{i=1}^m(y_i-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))x_{i1}\\ {\sum }_{i=1}^m(y_i-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))x_{i2}\\ ......\\ {\sum }_{i=1}^m(y_i-h({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}))x_{in}\end{array}\right]\end{array}$$
经过上述不断迭代的过程，最终得到一个合适的$\mathbf{w}$参数

4. 随机梯度上升

当数据量达到上亿或更多数据以后，梯度上升算法中的矩阵乘法等操作显然耗时将上升到非常高的程度
他通过随机取数据集中的部分数据，来代表整体数据集，从而实现对数据样本集的缩小，达到减少计算量，降低算法时间复杂度的目的。

三、代码实现

import numpy as np
import matplotlib.pyplot as plt
from random import randint


def sigmoid(in_x):
    """
    对列向量中的每个元素都执行一次sigmoid(x)函数

    :param in_x: 输入列向量
    :return: 函数值，列向量

    样例输入:
    [[0],
     [1],
     [2]]
     样例输出:
     [[sigmoid(0)],
      [sigmoid(1)],
      [sigmoid(2)]]
    """
    if in_x.any() >= 0:
        return 1.0/(1+np.exp(-in_x))
    else:
        return float(np.exp(in_x))/(1+np.exp(in_x))



def autoNorm(dataMat):
    """
    对数据进行归一化

    :param dataMat: 数据集
    :return: 数据集(归一化后)
    """
    minVals=np.min(dataMat, axis=0)
    maxVals=np.max(dataMat, axis=0)
    ranges=maxVals-minVals
    normDataSet=dataMat-minVals
    normDataSet=normDataSet/ranges#[0,1]
    return normDataSet


def load_data(filename):
    """
    从文件中加载数据

    :param filename:文件名称/路径
    :return: 数据集矩阵，数据类别标签向量
    """
    data_mat=[]
    data_labels=[]
    w0=[]
    with open(filename,'r')  as fr:
        for line in fr:
            currline=line.strip().split('\t')
            w0.append(1.0)
            data_mat.append(list(map(float, currline[:-1])))
            data_labels.append(float(currline[-1]))
        data_mat=autoNorm(np.mat(data_mat))
        data_mat=np.insert(data_mat, 0, values=np.mat(w0), axis=1)
    return data_mat, np.mat(data_labels).T


def get_weight_0(in_data_mat, in_data_labels, alph=0.01, r=500):
    """
    梯度上升算法

    :param in_data_mat: 输入训练集
    :param in_data_labels: 训练集标签
    :param alph: 移动步长
    :param r: 迭代多少次
    :return: w参数向量
    """
    shape=in_data_mat.shape
    weights = np.ones((shape[1], 1))
    for i in range(r):
        h_wx=sigmoid(in_data_mat*weights)
        err=in_data_labels-h_wx
        weights=weights+alph*in_data_mat.T*err
    return weights


def get_weight_1(in_data_mat, in_data_labels, c=0.01, r=50):
    """
    随机梯度上升(优化)

    :param in_data_mat: 输入训练集
    :param in_data_labels: 训练集标签
    :param c: 移动步长
    :param r: 迭代多少次
    :return: w参数向量
    """
    shape=in_data_mat.shape
    weights = np.ones((shape[1], 1))
    for j in range(r):
        index_list = list(range(shape[0]))
        for i in range(shape[0]):
            ran_num=randint(0, len(index_list)-1)
            index =index_list[ran_num]
            alph=4/(1.0+j+i)+c
            h_wx=float(sigmoid(in_data_mat[index]*weights))
            err=in_data_labels[index]-h_wx
            weights=weights+(alph*err*in_data_mat[index]).T
            del index_list[ran_num]
    return weights


def plot_fig(weights, in_data_mat, in_data_labels):
    """
    画出点集和所求的直线

    :param weights: w参数向量
    :param in_data_mat: 训练数据集
    :param in_data_labels: 训练集标签
    :return: None
    """
    size=in_data_mat.shape[0]
    for i in range(size):
        if int(in_data_labels[i]) == 0:
            plt.scatter(in_data_mat[i, 1], in_data_mat[i, 2], color='r', linewidth=5, marker='.')
        else:
            plt.scatter(in_data_mat[i, 1], in_data_mat[i, 2], color='b', linewidth=5, marker='.')
    weights=list(map(float, np.array(weights)))
    y=-(weights[0]+weights[1]*in_data_mat[:, 1])/weights[2]
    plt.plot(in_data_mat[:, 1], y, linewidth=5, linestyle='solid')
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.show()


def example_test():
    """
    测试函数

    :return:None
    """
    data_mat, data_labels=load_data('testSet.txt')
    weights=get_weight_0(data_mat, data_labels)
    plot_fig(weights, data_mat, data_labels)



example_test()