机器学习笔记-Task04-条件随机场CRF（Conditional Random Field）
文章目录
- 前言
- 1.相关概念
- 1.1有向图 VS 无向图
- 1.1.1有向图
- 1.1.2无向图
- 1.2 生成模型 VS判别模型
- 1.2.1 生成模型(generative model)
- 1.2.2判别模型（discriminative model）
- 2.隐Markov模型（HMM）
- 2.1Markov过程
- 2.2 隐Markov模型
- 2.2.1 两大假设
- 2.2.2五个要素
- 2.3问题
- 3.MEMM（最大熵Markov模型）
- 3.1特点
- 4.条件随机场CRF（Conditional Random Field）
- 4.1 介绍
- 4.2 CRF的概率密度函数
- 4.2.1推导过程
- 4.2.2向量表示
- 4.3CRF解决的问题
- 4.3.1 Learning问题-参数估计
- 4.3.2 Inference问题-边缘概率计算
- 4.3.3Inference问题-Decoding
- 参考资料
前言
条件随机场属于概率图模型的一种，为了详细了解条件随机场的前世今生，需要将HMM、MEMM和CRF放在一起学习，才够系统。ok，话不多说，让我们开始吧。
关于概率图模型的分类，可以参考下图。
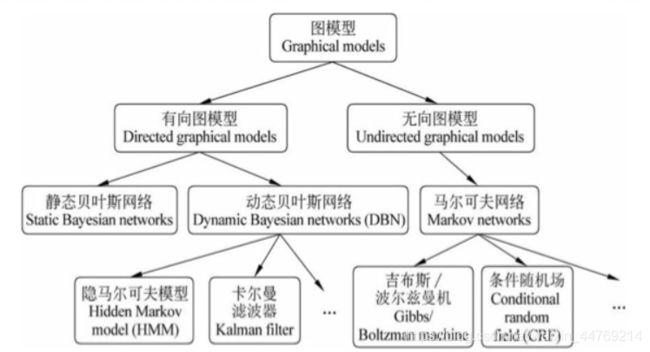
1.相关概念
1.1有向图 VS 无向图
对于二者的区别，主要体现在如何求概率。
1.1.1有向图
对于有向图，其联合概率的求法如下：
广义有向图的形式，如下图：
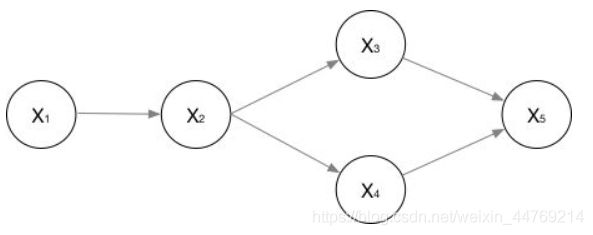
他们的联合概率可以表示为：
1.1.2无向图
无向图的表示，如下图：
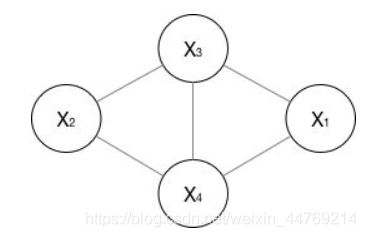
如果一个无向图太大，可以用因子分解将 P ( Y ) P(Y) P(Y)写为若干个联合概率的乘积。分解过程：将一个图分为若干个“小团”，注意每个团必须是“最大团”（我的理解：在最大团内，需要同时满足以下两个条件：（1）随机变量数要最多；（2）一个团内的所有随机变量之间要有联系，表示在图中的话，就是一个团内的任意两个随机变量之间要有连线），则有：
如上面的无向图，其概率为：
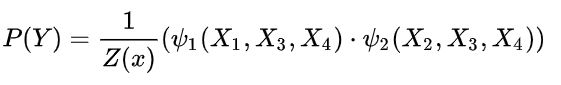
1.2 生成模型 VS判别模型
二者的区别主要在建模对象上
1.2.1 生成模型(generative model)
训练阶段是对 P ( X , Y ) P(X,Y) P(X,Y)建模，即求的是联合概率。
其有如下特点：
- 对 P ( X , Y ) P(X,Y) P(X,Y)建模
- 这里我们主要讲分类问题，所以是要对每个label（ y i y_{i} yi）都需要建模，最终选择最优概率的label为结果，所以没有什么判别边界。（对于序列标注问题，那只需要构件一个model）
- 中间生成联合分布，并可生成采样数据。
- 生成式模型的优点在于，所包含的信息非常齐全，我称之为“上帝信息”，所以不仅可以用来输入label，还可以干其他的事情。生成式模型关注结果是如何产生的。但是生成式模型需要非常充足的数据量以保证采样到了数据本来的面目，所以速度相比之下，慢。
1.2.2判别模型（discriminative model）
判别模型就是对 P ( Y ∣ X ) P(Y|X) P(Y∣X)建模，换句话说，直接根据X特征来对Y建模训练。所以判别式模型的特征总结如下：
- 对 P ( Y ∣ X ) P(Y|X) P(Y∣X)建模
- 对所有的样本只构建一个模型，确认总体判别边界
- 观测到输入什么特征，就预测最可能的label
- 另外，判别式的优点是：对数据量要求没生成式的严格，速度也会快，小数据量下准确率也会好些。
2.隐Markov模型（HMM）
2.1Markov过程
假设一个随机过程中， t t t 时刻的状态 y t y_{t} yt的条件分布，只与其前一状态 y t − 1 y_{t-1} yt−1 相关，即：
P ( y t ∣ y 1 , y 2 , . . . , y t − 1 ) = P ( y t ∣ y t − 1 ) P(y_{t}|y_{1},y_{2},...,y_{t-1})=P(y_{t}|y_{t-1}) P(yt∣y1,y2,...,yt−1)=P(yt∣yt−1)
则将其称为 Markov过程。
2.2 隐Markov模型
隐马尔科夫算法是对含有未知参数（隐状态）的马尔可夫链进行建模的生成模型，如下图所示。在HMM中存在隐状态 y t y_{t} yt（图中橙色部分）和观测状态 x t x_{t} xt（图中蓝色部分）。以词性标注为例，句子：小明爱中国。词性为名词+动词+名词。其中句子就是可以观测到的，是观测状态，而词性是需要标注，对我们而言是未知的，因此是隐状态。
2.2.1 两大假设
HMM中，有两大前提假设：
- 观测独立假设。即观测序列的各个状态仅取决于他所对应的隐状态。即 P ( x i ∣ y 1 , y 2 , . . . , y i + 1 , x 1 , x 2 , . . . , x i + 1 , . . . ) = P ( x i ∣ y i ) P(x_{i}|y_{1},y_{2},...,y_{i+1},x_{1},x_{2},...,x_{i+1},...)=P(x_{i}|y_{i}) P(xi∣y1,y2,...,yi+1,x1,x2,...,xi+1,...)=P(xi∣yi)
- 齐次马尔科夫假设。隐状态 y i y_{i} yi的状态满足马尔科夫过程， i i i时刻的状态 y i y_{i} yi 的条件分布，仅与其前一个状态 y i − 1 y_{i-1} yi−1 相关，即： P ( y i ∣ y 1 , y 2 , . . . y i − 1 ) = P ( y i ∣ y i − 1 ) P(y_{i}|y_{1},y_{2},...y_{i-1})=P(y_{i}|y_{i-1}) P(yi∣y1,y2,...yi−1)=P(yi∣yi−1)
这两大假设的目的，都是为了方便计算。
2.2.2五个要素
- 隐状态集；
- 观测状态集；
- 状态转移概率矩阵A；
- 观测概率矩阵B；
- 隐状态概率分布 π \pi π。
参数 λ = ( π , A , B ) \lambda =(\pi,A,B) λ=(π,A,B)
2.3问题
1.在序列标注问题中，隐状态（标注）不仅和单个观测状态相关，还和观察序列的长度、上下文等信息相关。例如词性标注问题中，一个词被标注为动词还是名词，不仅与它本身以及它前一个词的标注有关，还依赖于上下文中的其他词。
2.属于生成式模型，计算复杂
3.MEMM（最大熵Markov模型）
针对HMM中出现的问题，在MEEMM中，取消了HMM中的观测独立假设。（与HMM相比，注意 y i y_{i} yi与 x i x_{i} xi之间的箭头）
其概率图模型如下图所示，下面两幅图均可以表示。最上面一幅图中的 x g x_{g} xg表示全局观测变量：
或者
3.1特点
- 判别模型
- 因为局部归一化，存在标注偏差问题
4.条件随机场CRF（Conditional Random Field）
4.1 介绍
将MEMM的有向图模型，变为无向图模型，由此打破了HMM的齐次Markov假设，如下图所示（注意与MEMM图的隐状态序列 y i y_{i} yi对比）。CRF将MEMM的局部归一化变为了全局归一化，解决了MEMM中存在的标注偏差问题。
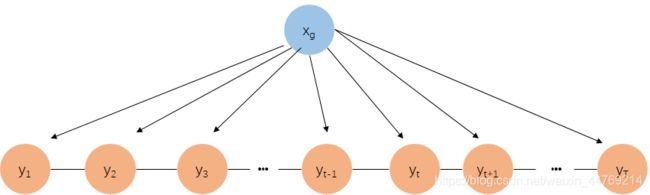
或者
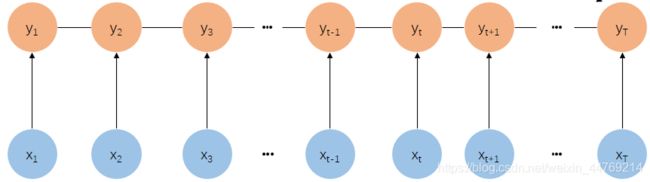CRF的特点：
- 判别式模型
- 无向图
4.2 CRF的概率密度函数
CRF 属于无向图、判别式模型，所以其概率密度函数为 P ( Y ∣ X ) P(Y|X) P(Y∣X).
根据无向图的概率计算，
P ( Y ∣ X ) = 1 Z ∏ i = 1 K ψ i ( x c i ) P(Y|X)=\frac{1}{Z}\prod_{i=1}^{K}\psi_{i}(x_{ci}) P(Y∣X)=Z1∏i=1Kψi(xci)
式中：
- K表示无向图中的最大团个数；
- ψ \psi ψ为势函数， ψ > 0 \psi>0 ψ>0
- x c i x_{ci} xci表示第i个团内所包含的随机变量
- 因为指数函数具有大于0的天然优势，所以一般用指数函数 e x e^{x} ex表示势函数，
因此上式可变为：
P ( Y ∣ X ) = 1 Z e x p ∑ i = 1 K F i ( x c i ) P(Y|X)=\frac{1}{Z}exp\sum_{i=1}^{K}F_{i}(x_{ci}) P(Y∣X)=Z1exp∑i=1KFi(xci)(指数函数连乘)
4.2.1推导过程
因此，CRF的概率密度函数是在观测序列 X X X给定的条件下，求条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X),其推导过程如下：
4.2.2向量表示
Ps:以上推导主要来自B站-白板推导。
4.3CRF解决的问题
概率图模型一般求解的问题主要分为两大类：Learning和Inference，共4个问题，如下图所示。但是因为CRF属于判别式模型，所以其解决的问题主要是图中红色对勾标注出来的。
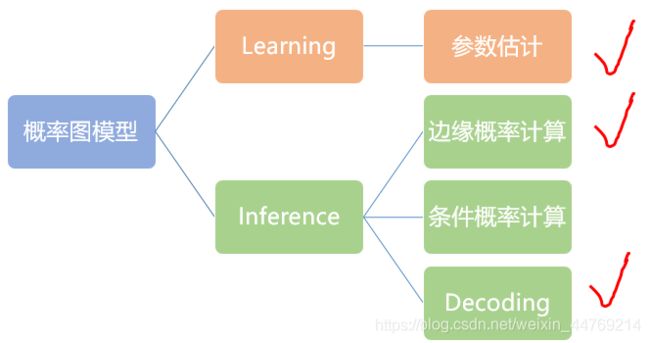
4.3.1 Learning问题-参数估计
已知有N个观测序列 X i X_{i} Xi，求解使得观测序列最大的模型参数。
θ ^ = a r g m a x ∏ i = 1 N P ( y ( i ) ∣ x ( i ) ) \hat{\theta}=argmax\prod_{i=1}^{N}P(y^{(i)}|x^{(i)}) θ^=argmax∏i=1NP(y(i)∣x(i))
4.3.2 Inference问题-边缘概率计算
即假定已经学习到了CRF的模型参数 θ \theta θ，求 P ( y t = i ∣ X ) P(y_{t}=i|X) P(yt=i∣X)
4.3.3Inference问题-Decoding
即序列标注，同HMM一样，使用Viterbi算法（动态规划）
参考资料
1.B站机器学习-白板推导系列(十七)-条件随机场CRF（Conditional Random Field）
2.知乎
Scofield[如何用简单易懂的例子解释条件随机场（CRF）模型？它和HMM有什么区别？]
3.简书【如何轻松愉快地理解条件随机场（CRF）?】