线性回归

1.1监督学习&无监督学习

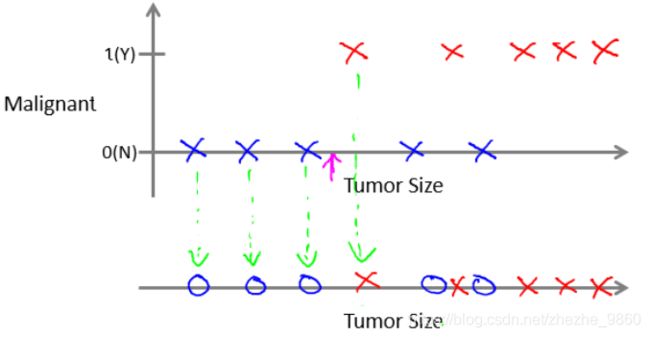
1.1.1监督学习Supervised learning

---

• 定义:从标注数据中学习预测模型的机器学习问题。
• 标注数据：表示输入输出的对应关系，预测模型对给定的输入产生对应的输出。
• 本质：监督学习的本质是学习输入输出的映射的统计规律。

---

• 监督学习的例子：房价预测 肿瘤良性预测问题
  • 房价预测（回归）
    
  • 肿瘤是否为良性预测（分类）
    

1.1.2无监督学习Unsupervised learning

---

• 定义：从无标注数据中学习预测模型的机器学习问题。
• 无标注数据：是自然得到的数据，预测模型表示数据的类别、转换或概率。
• 本质：无监督学习的本质是学习数据中的统计规律或潜在结构。

---

• 无监督学习的例子：
  • Google新闻（聚类）

1.2 单变量线性回归 Liner Regression with One Variable

• 导入模块包：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

• 读取数据：

path = 'ex1data1.txt'
data = pd.read_csv(path, header = None, names = ['Population','Profit'])
data.head() 

• 看一下数据：
  
• pd.read_csv()函数：
  • path: 文件路径
  • header: 指定第几行作为列名(忽略注解行)，如果没有指定列名，默认header=0; 如果指定了列名header=None
  • names:指定列名，如果文件中不包含header的行，应该显性表示header=None
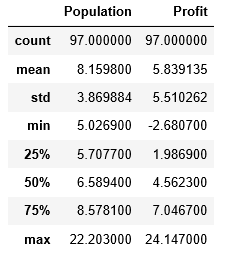
• 查看数据的统计数据：

data.describe() 

• 绘制数据散点图：

data.plot(kind = 'scatter',x='Population',y='Profit',figsize=(4,3)) #散点图 
plt.plot()

• 代价函数：均方误差函数
  $$J\left(\theta \right)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$$
  其中：
  $$h_{\theta }\left(x\right)={\theta }^{T}X={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$$

def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner)/(2 * len(X))

• 备注：为什么是$X\ast theta.T$？
  在这个程序中，X与T可能都是行向量，这个时候就要用X * theta.T，这样才会得到一个值而不是一个矩阵。而上述公式，是在X、theta都是列向量的情况下的结果。
• 在训练集中添加一列，以便可以使用向量化的解决方案来计算代价和梯度:

data.insert(0, 'Ones', 1)

• 变量初始化：

cols = data.shape[1] 
X = data.iloc[:,0:cols-1] 
y = data.iloc[:,cols-1:cols] 

• 计算代价函数：
  • 代价函数应该是numpy矩阵，所有需要转换X,y.然后才能使用它们还要初始化theta
  • theta初始值为0

X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0,0]))
computeCost(X,y,theta)

• 梯度下降算法：
  $${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J\left(\theta \right)$$
  $${\theta }_j={\theta }_j-\alpha \frac{1}{m}\sum _1^m{\left(h\left(x^i\right)-y^i\right)}^2{x}_j^i$$

def gradientDescent(X,y,theta,alpha,iters):#iters 迭代次数
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.ravel().shape[1])
    cost = np.zeros(iters)

    for i in range(iters):
        error = (X * theta.T) - y
        
        for j in range(parameters):
            term = np.multiply(error,X[:,j])
            temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))
            
        theta = temp
        cost[i] = computeCost(X,y,theta)
        
    return theta, cost

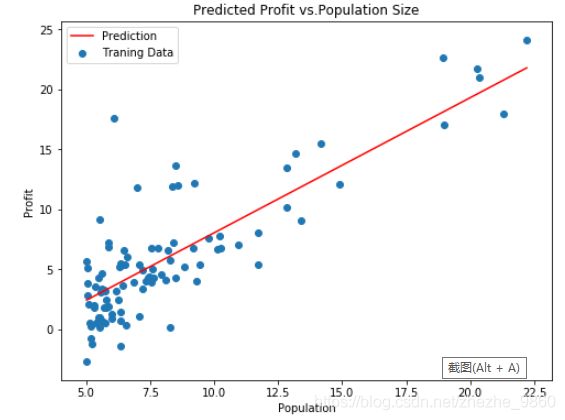
• 可视化显示：

x = np.linspace(data.Population.min(), data.Population.max(),100)
f = g[0,0] + (g[0,1] * x)

fig,ax = plt.subplots(figsize=(8,6))
ax.plot(x,f,'r',label='Prediction')
ax.scatter(data.Population,data.Profit,label='Traning Data')
ax.le()gend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs.Population Size')
plt.show

• 查看训练进程：

fig,ax = plt.subplots(figsize=(8,6))
ax.plot(np.arange(iters),cost,'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

1.3 多变量线性回归 Liner Regression with Multiple Variable

• 考虑房屋具有多个属性变量时（房间大小、卧室数量）预测房屋价格
• 读取数据：

path = 'ex1data2.txt'
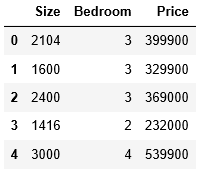
data2 = pd.read_csv(path, header = None,names=['Size','Bedroom','Price'])
data2.head()

• 特征缩放：

data2 = (data2 - data2.mean())/data2.std()
data2.head()

• 增加一列并计算代价值：

cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1] 
y2 = data2.iloc[:,cols-1:cols] 

#将X2 y2 转换为numpy矩阵 并 初始化theta2
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix(np.array([0,0,0]))

g2, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)
computeCost(X2, y2, g2)

-查看训练进程：

fig2,ax = plt.subplots(figsize=(4,3)) #subplots 加s!!!!!!
ax.plot(np.arange(iters), cost2, 'r')
ax.set_xlabel('Iteration')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch2')
plt.show()