前言
项目来自于Regonition System的一次assignment。
实现将一张以上的图片拼接为一张完整的全景图。
要求用Matlab完成,但不准使用任何第三方库、第三方代码,不准使用任务相关的内置函数(比如conv filter等)。
Main Steps
Task 1: Image Wrap: Cylindrical Projection
Task 2: Feature Extraction: Corner Point Detection
Task 3: Similarity Measurement: Distance Matching
Task 4: Random Sample Consensus (RANSAC)
Task 5: Merge
Task 1: Cylindrical Projection
Motivation
全景图一般以凸镜形式表示。这里用Cylindrical Projection对原图进行预处理,使得最后的拼接效果更自然。
其原理参考:百度百科:圆柱投影
Main Idea
将图片平铺在圆球的表面(但不覆盖最顶端),再投射到圆柱的表面,将其展开得到方形。
Formulation
Forward Transformation. img->img'
$$x'=f*tan^{-1}(\frac{x-\frac{W}{2}}{f})+f*tan^{-1}(\frac{W}{2*f})$$
$$y'=\frac{f*(y-\frac{H}{2})}{\sqrt{x-\frac{W}{2})^2+f^2}}+\frac{H}{2}$$
, 其中$(x',y')$是圆柱形坐标上的坐标位置,$f=\frac{W}{2*tan(\frac{\phi}{2})}$是相机中心(参数值),$\phi \in (0,\pi)$是用于调整变形程度的参数。
(以下图片来自用于实验HKUST校门图)![]()
Implementation
不能直接使用Forward Transformation。因为新坐标空间大于原始坐标空间,所以在新坐标空间中有许多位置在原空间没有对应的像素点,则导致 “black dot”。
要使用Reverse Transformation,Forward Transformation的逆函数。先得到圆柱形坐标空间中形变图像所占区域的bounding-box,再通过逆形变,获取新空间中每个位置在原空间中对应的坐标,填充完全。
Reverse Transformation Pseudo-Codes:
INPUT: Image I, degree of deformation $\phi$
1. Compute the new height H_, new width W_ of the projected image I_
2. for y_ in H_ do
for x_ in W_ do
x = reverse_transform(x_,$\phi$)
y = reverse_transform(x_,y_,$\phi$)
I_(x_,y_)=interpolation(x,y,I)
END for
END for
3. OUTPUT: Projected Result I_Interpolation
当x, y不是整数,无法对应原图任一pixel时,用插值方法间接计算非整型坐标上pixel的值。
1.bilinear interpolation
$I(x,y)=ax+by+cxy+d$
计算方法
对x y上下取整,4个新的坐标(x1,y1) (x1,y2) (x2,y1) (x2,y2)
分表带入式子,求得系数a b c d的值。
2.bicubic interpolation
$p(x,y)=\sum_{i=0}^{3}\sum_{i=0}^3a_{ij}x^iy^j$
计算方法一
a. 延展出总共4个式子,原式,偏导x,偏导y,偏导x y
b. 同1中取4个坐标,每个坐标都带入4个式子中
c. 总共得到16个式子,求解16个参数计算方法二
a. 对x y向下取整后,x-1:x+2, y-1:y+2,获得16个位置
b. 分别带入原式,求解16个参数
思想
$f(x)=ax^3+bx^2+cx+d$
$f'(x)=3ax^2+2bx+c$
偏导可以减少一个参数,在一维上两个值即可进行插值
Task 2: Corner Point Detection - Harris
Reference:
Trucco E, Verri A (1998) Introductory Techniques for 3-D Computer Vision. Upper Saddle River, NJ: Prentice Hall.
Motivation
角是一个重要的图像特征。
且一个角pixel没什么作用,要利用以其为中心的region patch。
Main Idea
当一个小窗口中包含了角点,这个窗向任意方向shift都会产生较大的intensity变化。![]()
Formulation
- 用数学方式表达shift后产生的intensity变化:
$E(u,v)=\sum_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2$
窗口经过$[u,v]$shift后,intensity变化的加权和。
当patches之间的变化非常明显,E值就会很大,符合Idea的描述。 - 近似推导

u,v要很小,利用taylor serious得到第二个约等式子。 - M, Harris Detector
且u,v和x,y无关、且固定,可以只考虑window weights和矩阵中间部分。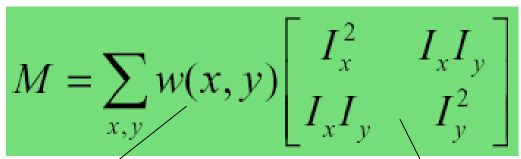
- Corner Response Measure
根据实验可以发现,patch内是否有角点与矩阵M的两个特征值有关,两个特征值需要同时比较大。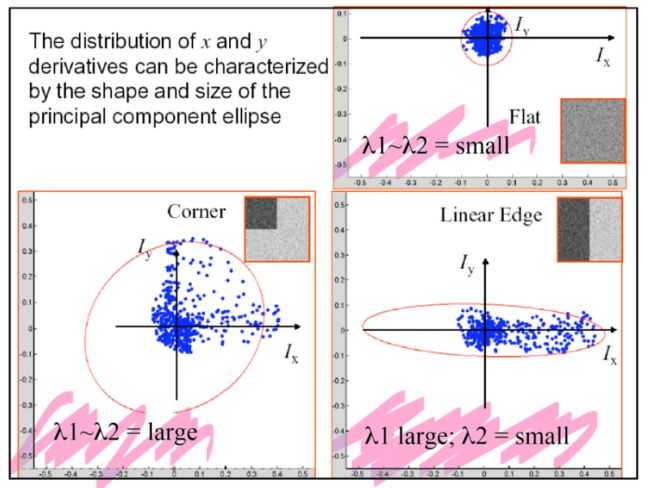
$R=detM-k(traceM)^2, k=0.04~0.06$
$detM=\lambda_1\lambda_2$
$traceM=\lambda_1+\lambda_2$
k越小,角点越细节,k越大,大而显著的角。
Implementation
Algorithm
- 1.计算图片每个Pixel的x,y偏导值
- 2.计算每个pixel上需要的products of derivatives
- 3.每个滑窗用Gaussian窗口加权,计算得到M矩阵
- 4.计算response值
- 5.Threshold response值
- 6.做nonmax suppression
角点及其所属region
光角点intensity是没有用的。
要在以角点为中心的region中,计算多种统计数据作为descriptor。
比如average intensity value, variance, pure intensity value, LBP值。
Task 3: Distance Matching
Motivation
将两张图片中的角点特征值在特征空间中做欧氏距离计算,当两个点之间的距离越短,说明他们越相似。
可以简单的以第一张图为基准,遍历第一张图的每个点,在第二张图中找到与之距离最短的点,然后删除第二张图的当前点;遍历第一张图的下一个点,做重复操作。
但是,假设第一张图中有点A C,第二张图中有点B。可能出现A B之间距离对于A来说最短,但B C之间的距离对于点B来说最短。这里就会产生不稳定的情况。
利用stable marriage相同的算法处理这种情况。
Main Idea
对于每张图片的每个点,都计算其和另一张图片中所有点的距离,排序。
以特征点少的图片为基准,遍历每个点。![]()
将Students全部放入待匹配列表,遍历。对于当前S1,尝试将其匹配给其排序中最短的Pa。
- 如果Pa没有匹配,就先将(Pa,S1)配对;
- 如果Pa已有匹配(Pa,S3),查看Pa的排序列表中S1是否先于S3,S1先于S3,则构成(Pa,S1)匹配,S3进入待匹配队列;
- 如果Pa已有匹配(Pa,S2),查看Pa的排序列表中S1是否先于S2,S1不先于S2,则尝试将S1匹配给其排序列表中下一个点Pc。
Validation
假设最终结果中的(i,j1) (i1,j)引发了不稳定性。则说明i比起j1更需要j,j比起i1更需要i。
但是结果表明i没有尝试匹配j,因为如果i更需要j,i会根据排序先和j匹配。contradiction。
如果如条件所说,i先跟j匹配会有(i,j),当轮到i1想和j匹配时,会因为j比起i1更需要i而拒绝i1的匹配。然而却有(i1,j)的存在。产生矛盾。
Task 4L Random Sample Consensus(RANSAC)
Reference
Multiple View Geometry in Computer Vision”, Second Edition. Richard Hartley and Andrew Zisserman, Cambridge University Press, March 2004.
Chapter 4. PP89 - 91
Motivation
寻找线性关系有几种方式:
- 解析几何
通过向量计算直接得到直线方程表达式(毫无误差) - 生产实践
问题:线性关系中也会出现一定的偏差。
思想:最小化模型预测值和测试纸的误差。
方法:最小二乘法,计算最小均方差,关于参数k,b的偏导数为0时的值。 - 复杂情况
问题:数据中有一定的噪音,且误差较大。
方法:RANSAC
Main Idea
给定一组观察数据(包含噪声或无效点),反复随机选择数据中的一组随机子集,作为inliers:
- 用当前inliers计算模型需要的参数
- 用模型测试所有数据,适用于这个模型的数据都属于inliers
- 如有足够多的点被认定为inliers,则认为模型合理
- 再根据所有inliers,用最小二乘法重新确定模型参数
- 用SSD loss模型评估模型
重复1-5。模型会因为#inliers过少、比当前最佳模型的loss大二被舍弃。
Formulation
这里是2D上计算。Homogeneous Computation。
映射方法:![]()
这里记录一下Homogeneous Solution。我用的是Imhomo的,这个计算方法不太了解。![]()
Implementation
随机取样取8个
Task 5: Merge
将基准图片作为基准,另一张图片做Homogeneous转换。
且将两个图片放置在统一的坐标上,重合部分作interpolation。(blending)