今天,我们来简单介绍一下深度优先搜索(DFS)的概念和使用。
在百度词条中,对深搜的解释是这样的。
由此,我们可知,深搜是广泛运用到 图 中的搜索方法之一。
用深度优先搜索遍历图的基本思路是:
(1)访问顶点v;
(2)依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
(3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。 当然,当人们刚刚掌握深度优先搜索的时候常常用它来走迷宫.事实上我们还有别的方法,那就是广度优先搜索(BFS,我们以后在做介绍).
但在今天,为了简化问题,我们不以 图 作为问题来论述 深搜 ,我们用排列组合的思想来运用 深搜。好,我们先来看一道问题。
显而易见,这道题可以使用循环来枚举每一个数字,但是这样需要用带9层循环,并且满足这样的数字还不只一个。如果使用这样的计算方式,会增加大量的时间复杂度(这里的时间复杂度(O)= n^9),给CPU很大的负担,甚至有些计算机系统不允许执行。
这道题也能在第一个数上从123遍历到333,然后计算出后面的第二个数,第三个数,然后再从中找出不重复的3个3位数,这是一个很好的方法,但是,这跟人用计算器来计算结果有什么区别?我们是要使用计算机从根本来解决这个问题。(这两种方法会在后面提供C\C++和JAVA的代码)
在这里,我们重点讲述更为合理的深度优先搜索方法。这里需要用到 排列组合 的思想,我们先来解释3个数的排列组合,再来类比题目中的9个数的排列组合。
这里我们假设有3个盒子,分别标记上1号,2号,3号。我们现在需要把1、2和3,这三个数字放在其中,有多少种放法呢?这个很简单,即便是没有学过排列组合都能计算出多少种放法。我们先来枚举出组成的3位数吧,有123、132、213、231、321、312,共6种放法。然而,我们只需要运算 3*2*1 ,就能得到有6种放法,但是计算机应该怎么去计算呢?
这里,我们请一个叫小曦的同学帮忙,让他模拟计算机运行,我们给他规定好方法。
首先,小曦手中有3张标着有1、2、和3的卡片,面前有如上图所示的盒子。我们让小曦先去1号盒放一张卡片,再让小曦走到下一个盒子,也就是2号盒放一张卡片,最后到3号盒子放最后一张,即便是后面还有盒子,但小曦手中没有卡片了,也是无法去放的。
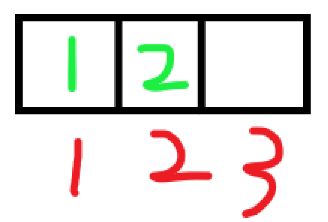
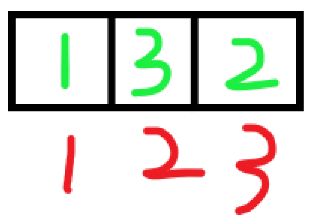
现在,我们让小曦开始去放卡片,小曦来到1号盒子前,果断的放了标有1的卡片,然后来到2号盒子前,放了标有2的卡片,最后,小曦只能在第3号盒子放进标有3的卡片。这样,就形成了一个3位数的数字——123。我们记录下这个数字,让小曦收回放在盒子的卡片,这个时候,小曦正好在3号盒子前,所以小曦拿起了3号盒子中的标有3的卡片,然后退回到紧挨着3号盒子的2号盒子,拿起了2号盒子中标记着数字2的卡片,这时候,小曦的手中拿着有标记着2、3数字的两张卡片,小曦发现,手中的数字3卡片还没有放在过盒子2号中,于是小曦将手中的数字3卡片放在2号盒子中,然后来到3号盒子前,只能把数字2的卡片放在3号盒子中。这时,就形成了第二个3位数——132。我们再将132记录好。让小曦收回卡片,小曦按照原来的方法,走回2号盒子前收回数字3卡片后,发现2、3都已经放在盒子里面过了,于是小曦只好退回到1号盒子前收回数字1的卡片,然后发现1号盒子里面还未放过数字2、3的卡片,于是放进了数字2的卡片。(类似于栈一样,后进先出)
就这样,小曦一直重复着这一过程,最终得到123、132、213、231、321、312,6种的放法。我们把图放上来,方便大家理解。
后面图略。。。
现在,我们按照题中的要求,把3个数扩展到9个数。
还是按照小曦放3个数字的方法来放9个数字。然后让1、2、3号盒子构成的数字与4、5、6号和7、8、9号盒子构成的数字形成如题所示的方式,这样,1到9的数字不会重复出现。好,我们先把代码搬上来。
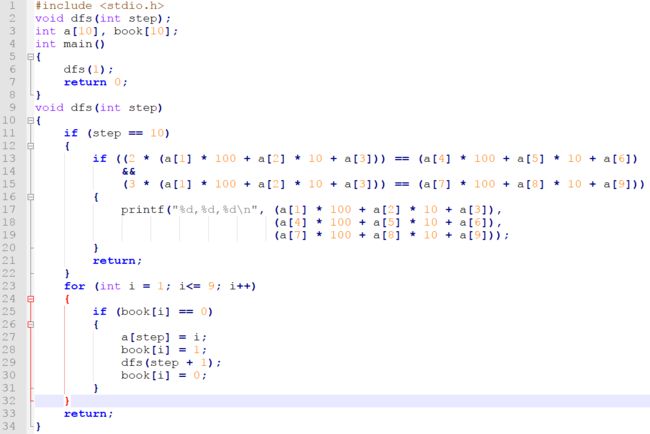
这里,我使用了私有的全局的内部类来保存深度优先搜索算法,供主函数调用,并用static保存全局变量。显然,深搜的核心就是方法(函数)的递归。我们下面来介绍步骤。
这里解释一下,这里构造器构造出指定了长度的数组在没有赋值以前默认为0。C\C++中,全局变量在没有赋值以前也是默认为0。所以这里不需要再初始化为0。我们在这里构造了卡片和盒子,a的下标表示几号盒子,book的下标表示卡片上的数字(类似于桶排序的方法)。
这里用了book来标记卡片是否已经放在盒子中,而在book中间的toBeUsed回调,则是往下一个盒子移动。
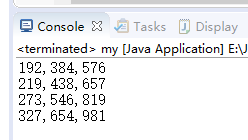
到这里基本就已经解决问题,如果还是无法深搜的概念,可以反复理解这段代码。下面,我们提供C\C++的代码。
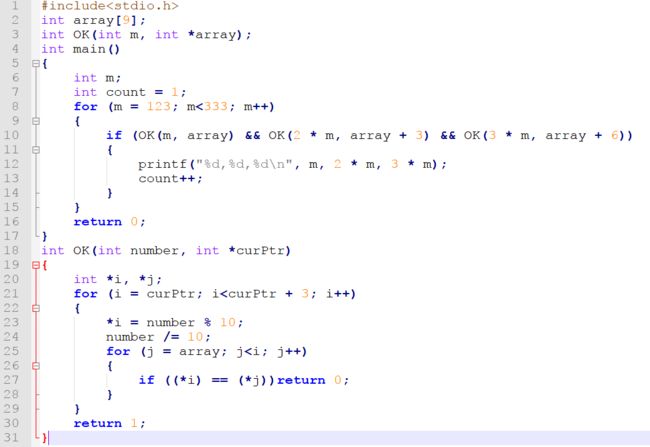
我们来看第二种方法的C\C++代码,JAVA代码这里省略。(基本一样)
这里使用了指针来读取每一个得到数,并保存在array数组中,每保存一个数的时候,就判断是否存在重复的。
九重循环的枚举方法就在这里省略。
注:mooc上的编译器可能存在问题,不支持复杂的运算。也可能是超时问题(几率很小)。