关于万向节死锁(Gimbal Lock)

在http://blog.donews.com/wanderpoet/archive/2005/07/04/453608.aspx
看到一篇关于Gimbal Lock的E文，解释得挺清楚的，翻译如下：

Gimbal Lock

。。。
Maybe it's a bit difficult to understand. OK, let me show you a real sence.

可能有点不好理解。让我们看个现实中的场景。

Say that we have a telescope and a tripod to put the telescope on. The tripod is put on the ground. The top of the tripod holding the telescope is leveled with the horizon (reference plane) so that a vertical rotation axis (we call it X axis) is perfectly vertical to the ground plane. The telescope can then be rotated around 360 degrees in X axis so that it can scan the horizon in all the directions of the compass. Zero degrees azimuth is usually set toward a heading of true north. A second horizontal axis parallel to the ground plane (we call it Y axis), enables the telescope to be rotated in elevation upward or downward from the horizon. The horizon is usually set at zero degrees and the telescope can be rotated +90 degrees upward in elevation so that it is looking straight up toward the zenith or rotated -90 degrees downward so that it is looking vertically at the ground plane.

假如我们有一个望远镜和一个用来放望远镜的三脚架，（我们将）三脚架放在地面上，使支撑望远镜的三脚架的顶部是平行于地平面（参考平面）的，以便使得竖向的旋转轴（记为x轴）是完全地垂直于地平面的。现在，我们就可以将望远镜饶x轴旋转360度，从而观察（以望远镜为中心的）水平包围圈的所有方向。通常将正北朝向方位角度记为0度方位角。第二个坐标轴，即平行于地平面的横向的坐标轴（记为y轴）使得望远镜可以饶着它上下旋转，通常将地平面朝向的仰角记为0度，这样，望远镜可以向上仰+90度指向天顶，或者向下-90度指向脚底。

OK, that's all we needed. every point in the sky (and the ground) can be referenced by only ONE unique pair of X and Y readings. For example an X of 90 degrees and Y of 45 degrees specifies a point exactly due east of the telescope and in a skyward direction half way up toward the zenith.

好了，万事俱备。现在，天空中（包括地面上）的每个点只需要唯一的一对x和y度数就可以确定。比如x=90度,y=45度指向的点是位于正东方向的半天空上。

Now let me show you how the gimal lock occurred. We detect a high flying aircraft, near the horizon, due east from the telescope (X = 90 degrees, Y = 10 degrees) and we follow it (track it) as it comes directly toward us. The X angle stays at 90 degrees and the Y angle slowly increases. As the aircraft comes closer the Y angle increases more rapidly and just as the aircraft reaches an Y of 90 degrees (exactly overhead), it makes a sharp turn due south. We find that we cannot quickly move the telescope toward the south because the Y angle is exactly +90 degrees so we loose sight (loose track) of the aircraft . We have GIMBAL LOCK!

现在，看看万向节死锁是怎么发生的。一次，我们探测到有一个飞行器贴地飞行，位于望远镜的正东方向（x=90度，y=10度），朝着我们直飞过来，我们跟踪它。飞行器飞行方向是保持x轴角度90度不变，而y向的角度在慢慢增大。随着飞行器的临近，y轴角增长的越来越快且当y向的角度达到90度时（即将超越），突然它急转弯朝南飞去。这时，我们发现我们不能将望远镜朝向南方，因为此时y向已经是90度，造成我们失去跟踪目标。这就是万向节死锁！

(译注：为什么说不能将望远镜朝向南方呢，让我们看看坐标变化，从开始的（x=90度，y=10度）到（x=90度，y=90度），这个过程没有问题，望远镜慢慢转动跟踪飞行器。当飞行器到达（x=90度，y=90度）后，坐标突然变成（x=180度，y=90度）（因为朝南），x由90突变成180度,所以望远镜需要饶垂直轴向x轴旋转180-90=90度以便追上飞行器,但此时，望远镜已经是平行于x轴，我们知道饶平行于自身的中轴线的的旋转改变不了朝向，就象拧螺丝一样，螺丝头的指向不变。所以望远镜的指向还是天顶。而后由于飞行器飞远，坐标变成（x=180度，y<90度）时，y向角减小，望远镜只能又转回到正东指向，望'器'兴叹。这说明用x,y旋转角（又称欧拉角）来定向物体有时并不能按照你想像的那样工作，象上面的例子中从（x=90度，y=10度）到（x=90度，y=90度），坐标值的变化和飞行器空间的位置变化一一对应，但是从（x=90度，y=90度）到（x=180度，y=90度），再到（x=180度，y<90度）这个变化，飞行器位置是连续的变化，但坐标值的变化却不是连续的（从90突变到180），其原因在于（x=90度，y=90度）和（x=180度，y=90度）甚至和（x=任意度，y=90度）这些不同的坐标值对应空间同一个位置，这种多个坐标值对应同一个位置的不一致性是造成死锁的根源。【感谢zeroyear, fatfatson 等的深层解释，原先解释的不够清晰，故修改如上。原文：按照欧拉角旋转确实可以正确地定向，但从（x=90度，y=90度）到（x=180度，y=90度），再到（x=180度，y<90度）,按照欧拉角旋转后的定向并非正确】)

It's a example of 2D coordinate frame. It's very similar in 3D frame. We say that you have a vector which is parellel to the X axis. And we rotate it around  Y axis so that the vector is parellel to the Z axis. Then we find that any rotations around  Z axis will have no effect on the vector. We say that we have a GIMBAL LOCK

上面是2维坐标系中的例子，同样，对于3维的也一样。比如有一个平行于x轴的向量，我们先将它饶y旋转直到它平行于z轴，这时，我们会发现任何饶z的旋转都改变不了向量的方向，即万向节死锁。

(译注：3维的万向节死锁情况分析见：http://www.cnblogs.com/soroman/archive/2008/03/24/1118996.html)

 

以前发过一篇文章http://www.cnblogs.com/soroman/archive/2006/10/11/526163.html是关于万向节死锁(Gimbal Lock)的，里面翻译了2维坐标系中的万向节死锁问题的阐述。后来，参考了各位bloger的观点以及一些资料，整理了一下3维下的Gimbal Lock问题，算是加深一下理解吧，如下：

在3维中常用的欧拉角坐标定向系统是用绕三个轴旋转的角度来表示物体的朝向(Rx,Ry,Rz)（注意三个轴是针对物体坐标系的）。如图1，物体处于世界坐标系（Xw,Yw,Zw）原点，此时物体坐标系(Xl,Yl,Zl)和世界坐标系重合（这里我使用右手坐标系。你也可以使用左手坐标系，无所谓，一样）。此时，规定物体的朝向为（0,0,0）。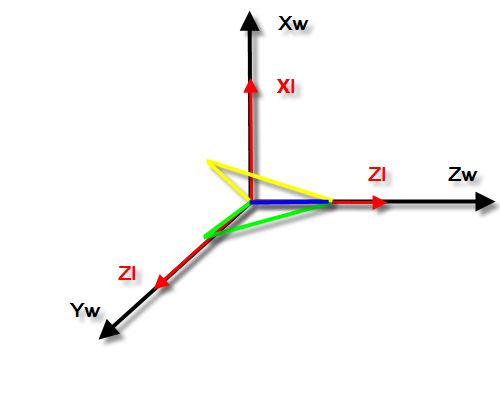


图1：物体的初始朝向

现在开始旋转物体，先绕物体坐标系x轴(Xl)旋转30度（这里我规定沿着轴向轴的负方向看去，顺时针旋转为正。你也可以自己规定，无所谓，遵守规定即可），注意，此时的物体坐标系已经发生变化，见图2，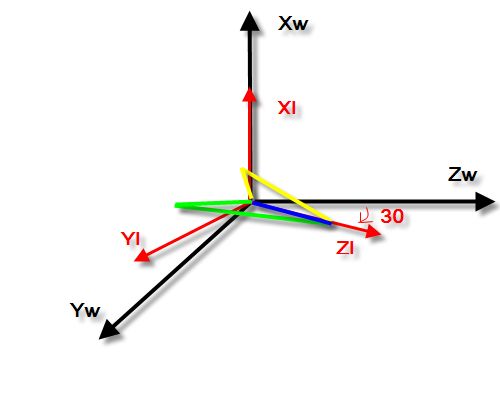


图2：物体绕物体坐标系x轴(Xl)旋转30度

然后再绕Yl轴旋转90度，此时，你会发现Zl轴已经和了世界坐标系X轴共轴。见图3。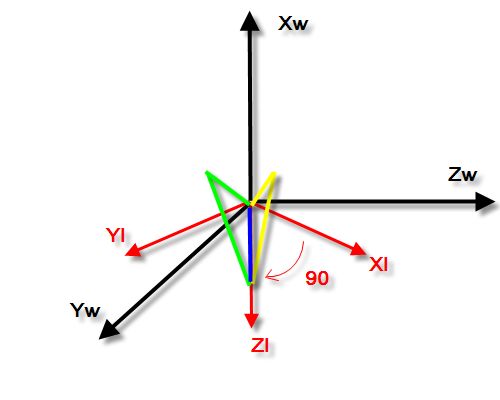

图3：物体绕物体坐标系y轴(Yl)旋转90度

好了，此时使用欧拉角来表示当前物体的方向的话，其坐标应该是（30,90,0），对应旋转顺序是Xl->Yl->Zl。然而，有意思的是如果再继续旋转，现在按照Zl旋转-40度，发现什么了？咦，怎么感觉已经绕过这个轴旋转过一次了，虽然轴向相反？^_^,anyway,最后的坐标应该是（30,90,-40），见图4。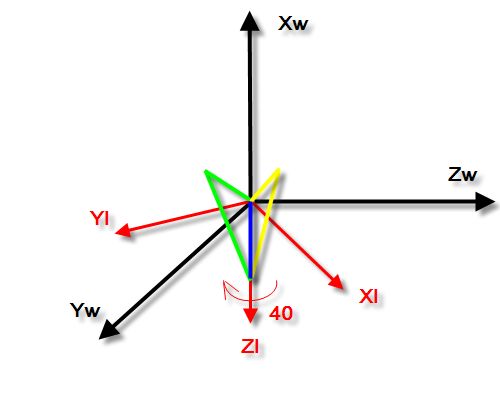

图4：物体绕物体坐标系z轴(Zl)旋转-40度

好了，回到刚才的疑惑上，既然感觉两次旋转是绕同一轴，如果我一开始考虑全部绕该轴的旋转呢？即先绕Xl旋转30-(-40)=70度，然后再绕Yl旋转90度。^_^怎么样，已经到达和上次旋转的效果了吧。这说明什么？欧拉角坐标（30,90,-40）和（30-(-40),90,0）等同。甚至坐标（Rx1,90,Rz1）和（Rx2,90,Rz2）相同，只需满足Rx1-Rz1=Rx2-Rz2。当Rx1-Rz1=Rx2时，Rz2==0，即在这种情况下任何再绕Zl轴的旋转，都可以使用先绕Xl轴来做到。或者从另一个角度来说，物体现在本质上只能绕两个轴的旋转！即少了一个旋转自由度！这就是3维中的万向节死锁现象。

概括起来可以这么说，绕着物体坐标系中某一个轴，比如y轴的+(-)90度的某次旋转，使得这次旋转的前一次绕物体坐标系x轴的旋转和这次旋转的后一次绕物体坐标系z轴的旋转的两个旋转轴是一样（一样的意思是指在世界坐标系中，两次旋转轴是共轴的但方向相反）,从而造成一个旋转自由度丢失。

实际上，使用3个量来表示3维空间的朝向的系统都会遭遇这个问题，除非用4个量来表示，如四元数。

2维的情况下欧拉角系统的万向节死锁导致了望远镜不能跟踪飞行器的位置，用某人的话就是在某种坐标系统下，空间中连续的的位置，不能用连续的坐标值来表示。看看3维情况下是不是也是这样？是不是不能跟踪飞行器的朝向？

举例：飞行器开始的方向是如图1所示，对应欧拉角坐标（0，0，0）。现在飞行器按照绕Xl 30度，然后绕Yl 40度，最后绕Zl 50度的顺序旋转，对应地，欧拉角坐标来跟踪的话是(30,40,50)。最后飞行器的朝向是如图5所示。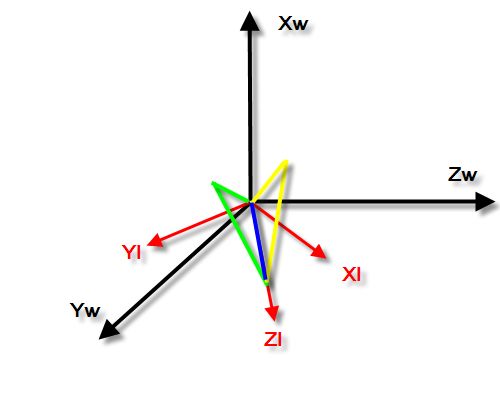

图5：坐标(30,40,50)对应的朝向

现在，飞行器又开始绕Xl轴转个1度。那么现在，欧拉坐标相应地变成(31,40,50)来跟踪，这个坐标对应的飞行器的朝向对吗？实际上是对的，没有问题，一切OK。

换个情况，飞行器从图1初始位置按照绕Xl 30度，然后绕Yl 90度，最后绕Zl -40度的顺序旋转，对应地，欧拉角坐标来跟踪的话是(30,90,-40)，最后飞行器的朝向是如图4所示。现在，飞行器又开始绕Xl轴转个1度。那么现在，欧拉坐标相应地变成(31,90,-40)来跟踪，对吗？比划看看，使用这个坐标，飞行器肯定对不上了！万向节死锁还是那么讨厌。

这也是为什么3维的情况下，欧拉角插值不适合用来表示旋转插值（等角速度）的原因。使用四元数插值吧，可以参考：http://www.cnblogs.com/soroman/archive/2006/09/19/509597.html