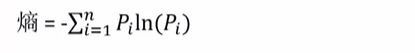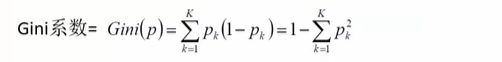R语言第十一讲 决策树与随机森林
概念
决策树主要有树的回归和分类方法,这些方法主要根据分层和分割 的方式将预测变量空间划分为一系列简单区域。对某个给定待预测的观 测值,用它所属区域中训练集的平均值或众数对其进行预测。
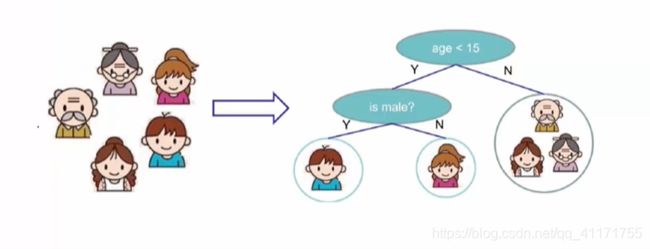
如图所示,一共有5个人,我们根据年龄和性别进行判断,这个人是否喜欢打篮球。我们首先根据年龄是否大于15来判断是否喜欢打篮球。如上,判断出年龄大于15的都不喜欢打篮球,年龄小于15的可能喜欢打篮球。第一次划分,左边的数据集还具有不确定性,因此,我们再次根据性别进行划分,直到叶子节点的数据集的纯度较高时,停止划分。如上的树就是一棵决策树,决策之意,就是我们在每个分支节点上都定义了一个决策属性(age、is male)。使用方法:我们只需要将数据集中的每一个样本从上往下依次去走,直至到达叶子节点,来求得其预测值。
真正的叶子节点的数据集的预测值往往达不到纯度(预测值数据占此叶子节点数据集的百分比)为100%,假设响应变量(是否打篮球)为定性变量,那么其响应值就是叶子节点数据集中出现次数最多的响应值,我们假设爷爷奶奶不喜欢打篮球,他妈妈喜欢打篮球,那么此叶子节点其响应值就是不喜欢打篮球。假设响应变量为定量变量(连续的数值类型),那么其响应值就是此叶子节点所有响应值的加权平均数。
决策树,为什么要先用age决策呢,决策树如何建立的呢?
接下来,我讲一讲决策树的训练阶段。如何从给定的数据集中构造出一棵决策树?
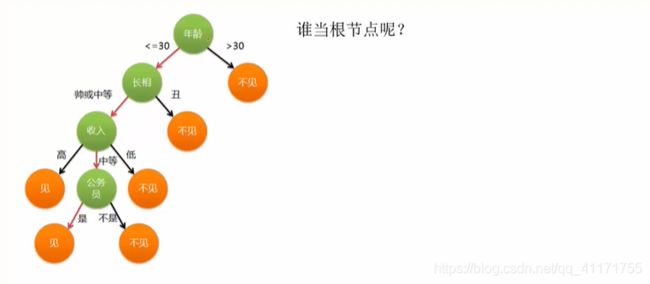
如上图,假设这是一个人要去见约会对象了,我们将根据约会对象的年龄、长相、收入、是否是公务员来预测其去不去见他的约会对象。首先看年龄,其次看长相,再其次看收入……,决策的先后代表其重要的程度。
熵 :描述一个子数据集的纯度指标。pi代表的是第i个响应值在叶子数据集中所占的比例,一共有n种响应值。从以下的公式,我们能够的出,如果一个数据集的纯度越高,其熵值就会越低,反之,越高。
基尼系数: 描述一个子数据集的纯度指标。,如果一个数据集的纯度越高,其基尼系数值就会越低,反之,越高。
到底谁来当根节点,这个是由计算机内部计算出来的。
构造决策树的基本思想:随着树深度的增加,节点的熵值迅速的降低熵值降低的越快越好,这样就能得到一颗高度最矮的决策树。
下面通过一个例子,来介绍决策树的构造过程。
预测变量为:outlook(天气)、temperature(温度)、humidity(湿度)、windy(是否有风)。
响应变量:是否出去玩(play)
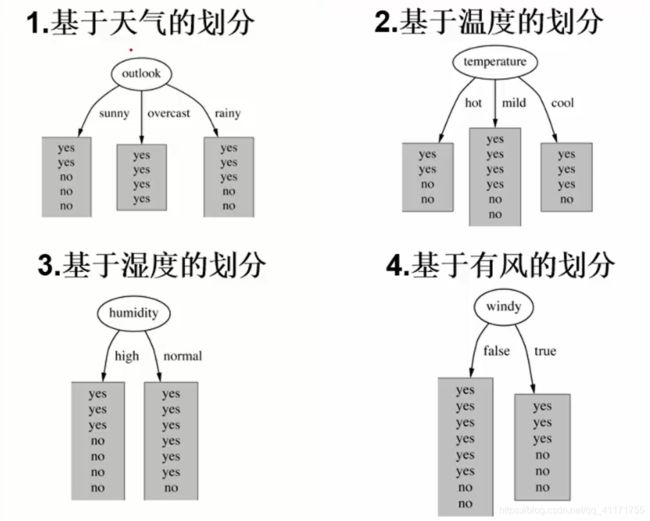
构造决策树:谁来当根节点?我们的得到如下的四种划分。
上面说过了,决策树的构造是根据随着树深度的增加,节点的熵值迅速的降低熵值降低的越快越好。那么这四种划分,那种的熵值降低的幅度最大呢?原有数据集的熵值如下公式计算出来。
首先呢,若选择outlook作为根节点,首次划分之后,其熵值为多少呢?
outlook一共有14个样本
outlook=sunny时,5个样本,2/5的概率打球,3/5的概率不打球。entropy=0.971
outlook=overcast时,4个样本,entropy = 0
outlook=rainy时,5个样本,entropy= 0.971.
其熵值为:5/14 x 0.971 + 4/14 x 0 + 5/14 x 0.971 = 0.693。
如此,系统熵就从0.940降到了0.693.信息增益为 0.940 - 0.693 = 0.247
同样的temperature 信息增益为0.029,humidity 信息增益为0.152,windy 信息增益为0.048.
谁的信息增益大,取那个特征做决策,递归的其左右孩子皆为如此。
接下来,介绍一下一种算法叫做ID3算法,决策树传统的算法,他就是利用信息增益来构建决策树。
信息增益看起来很好,但其实他是存在一些问题的。它存在一些异常现象。
假设,我们考虑这样一个特征,他呢,有很多个值,每一个属性值内部的样本数量又非常少,极端情况下,其每一个属性值内部只有一个样本,那么其熵值就会为0,但是,这样的特征真的就好吗。答案是否定的。采用信息增益作为判定方法,会倾向于去选择属性取值比较多的属性。那么,选择取值多的属性为什么就不好了呢?举个比较极端的例子,如果将身份证号作为一个属性,那么,其实每个人的身份证号都是不相同的,也就是说,有多少个人,就有多少种取值,它的取值很多吧,让我们继续看,如果用身份证号这个属性去划分原数据集D,那么,原数据集D中有多少个样本,就会被划分为多少个子集,每个子集只有一个人,这种极端情况下,因为一个人只可能属于一种类别,好人,或者坏人,那么此时每个子集的信息熵就是0了,就是说此时每个子集都特别纯。信息增益计算出来的特别大,然后决策树会用身份证号这个属性来划分原数据集D,其实这种划分毫无意义。
所以,后人提出了对于ID3的改进算法:C4.5,他是基于信息增益率来构造决策树的。
信息增益率:一个决策的信息增益/属性的熵值
比如身份证的例子,身份证属性的熵值就很大,因为其属性值很多,纯度很低。身份证的熵值虽然大但是除以属性的熵值之后就会变小,也就是其信息增益率就会很小。
如何评价一棵决策树的预测效果呢,到底这颗树的效果如何呢?
在此,我们引入评价函数
N代表当前叶子节点数据集的样本数量,H代表当前叶子节点的熵值。
树的减枝。一个决策树预测好了之后,如果不进行减枝很可能会出现过拟合的现象发生,也就是说,他能很好的拟合训练集,但是测试集的运行效果并不是很好,这主要在于这棵树太过于庞大,有太多的分支,也可能是受到了训练集上一些异常值的影响。
我们可以进行两种减枝操作:
预剪枝:在构建决策树的过程中,提前停止。比如,决策度的深度、或者某个叶子节点数据集样本数到某个数值时就进行停止。
后剪枝:决策树构建好了后,然后才开始减枝。我们将评价函数作如下改变, T代表叶子节点的个数。
图中的a值用来,作为一个调整参数。
我们利用评价函数,对树中的分支节点进行评价,根据评价函数值进行决定要不要进行减枝。
随机森林:通俗的讲就是我们将训练集中部分数据进行10次有放回的随机抽样得到十个训练集,然后就能在十个训练集上得到十棵决策树,构造决策树的时候,选择特征(天气、温度……)时,每棵树只抽取部分特征。使用的时候,用十棵决策树共同来做出决定,比如同一个预测变量值,六棵树预测为蓝色,4棵为红色,其最终预测值就是蓝色。