An Intuitive Introduction to Global Illumination and Path Tracing

https://www.scratchapixel.com/lessons/3d-basic-rendering/global-illumination-path-tracing/introduction-global-illumination-path-tracing

in this lesson we will use Monte Carlo methods to simulate global illumination. it will be hard if not impossible to understand this lesson fully if u are not familiar with Monte Carlo methods.
hopefully for u, we have covered this topic extensively in the section the mathematics of computer graphics. read these lessons first before proceeding.

what is global illumination anyway?
global illumination is actually pretty simple to simulate. though generally, the main or principal issue with global illumination is that no matter what u do, it is generally very expensive to simulate and difficult to simulate efficiency.

but what is global illumination in the first place anyway? as u know, we see things because light emitted by light sources such as the sun bounces off of the surface of objects. when light rays bounce only once from the surface of an object to reach the eye, we speak of direct illumination. but when light rays are emitted by a light source, they can bounce off of the surface of objects multiple times before reaching the eye. this is what we call indirect illumination because light rays follow complex paths before entering the eye. this effect is clearly visible in the images above. some surfaces are not exposed directly to any light sources (often the sun), and yet they are not completely black. this is because they still receive some light as an effect of light bouncing around from surface to surface.

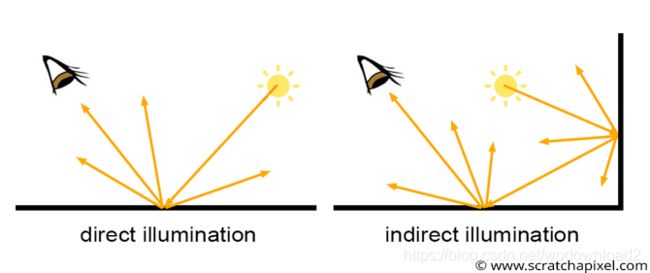
so far, we learned about simulating direct illumination. global illumination involves to simulate both effects: direct plus indirect illumination. simulating both effects is important to produce realistic images.

being able to simulate global illumination seems like a feature that every rendering system should have so why making a big deal out of it? 看起来全局照明应该是每个渲染系统的特性，但是为啥还有小题大做呢？because while simple in some cases, it is complex to solve in a generic manner and also generally expensive. this explains why for example most real-time rendering systems do not offer to simulate (at least accurately) global illumination effects.

1. it is hard to come with a generic solution that solves all light paths: light rays can interact with many different kind of materials before entering the eye. for example a light ray freshly emitted from a light source may be reflected by a diffuse surface first, then travel though a glass of water (it has been refracted then which menas a slight shift or change of direction), then hit a metal surface, then another diffuse surface and then finally hit the eye. there is an infinity of possible combinations. the path that a light ray follows from the light source to the eye is simply called a light path. as u know, in the real world, light travels from light sources to the eye. from a mathematical point of view, we know the rules that define the way light rays are reflected off from the surface of various materials. for example we know about the law of reflection, we know about refractoin, etc. simulating the path of a light ray as it interacts with various materials is thus something that we can easily do with a computer. though the problem as u know, is that forward tracing in computer graphics is not an efficient way of making up an image. simulating the path of light rays from the light source they are emitted from to the eye is inefficient (see the lesson Introduction to Ray Tracing: a Simple Method for Creating 3D Images). we prefer backward tracing which consists of tracing the path of light rays from the eye, back to the light source where they originated from. the problem is that backward tracing is an efficient way of computing direct illumination indeed but not always an efficient way of simulating indirect lighting. we will show why in this lesson.
   
   Figure 2: simulating indirect diffuse using backward ray-tracing.

2. direct lighting mostly involves to cast shadow rays from the shared point to the various light sources contained in the scene. how fast computing direct lighting is depends directly on the number of light sources contained in the scene. though computing indirect lighting is generally many times slower than computing direct lighting because it requires to simualte the path of a great number of additional light rays boucing around the scene. generally, simulating these light paths can be more easily done with rays and ray-tracing though ray-tracing as we also know is quite expensive. as we progress with the lesson, understanding why simulating global illumination is an expensive process will become clearer.
   What you need to remember from this part of the lesson, is essentially that there is two ways for an object to receive light: it can receive light directly from a light source or indirectly from other objects. Objects in a way can also been seen as light sources. Not because they emit light though but because they reflect light. Thus we need to take them into consideration when we compute the amount of light a shaded point receives (of course, to reflect light these objects need to be illuminated themselves somehow either directly or indirectly). You may guess that this is a complex problem on its own because light reflected by an object A towards an object B might be reflected by B back to A, which in turns will reflect some of that light again back to B, etc. The lighting of B depends on A, but the lighting of A also depends on B (figure 3). The process implies an exchange of energy between surfaces which can go for ever. Putting this in mathematical form is possible, but solving the resulting equations is much harder (for a more formal introduction to this topic check the lesson devoted to the Rendering Equation in the next sections).
   Simulating indirect illumination is about simulating the paths that light rays take from the moment they are emitted by a light source to the moment they enter the eyes. For this particular reasons we generally speak of light transport, the transport of light or its propagation in space as it bounces from surface to surface. A light transport algorithm (backward tracing which we will talk about again this chapter is an example of such algorithm) is an algorithm that describes how this light transport problem can be solved. As you we will explain in this lesson, simulating light transport is a complex problem, and it is hard to come with one algorithm that makes it possible to describe all sort of light paths that we find in the real world.
   
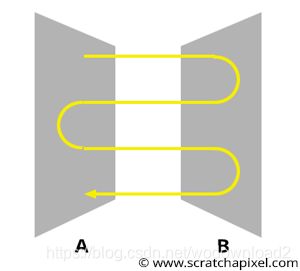
   Figure 3: exchange of light energy between two unoccluded patches. Illumination of B depends on the light reflected or emitted by A in the direction of B, but some of that light is reflected back to B which reflects it again to A, etc.

How Do We Simulate Indirect Lighting with Backward Tracing
To understand the problem of simulating global illumination with backward tracing, you first need to understand how we can simulate indirect lighting. As suggested, many attempts have been made to formalize this process i.e. putting the process into a mathematical form (interested and mathematically savvy readers can fine some information in the reference section at the end of this lesson). Though, we will first explain the process in simple terms. If you are interested in the maths, please check the advanced lessons on rendering in the next sections.

we know from the previous lesson that light illuminating a given point P on the surface of an object, can come from all possible directions contained within a hemisphere oriented about the surface normal N at P. when u deal with direct light sources, finding where light comes from is simple. we just need to loop over all the light sources contained in the scene and either consider their direction if it is a directional light or trace a line from the light source to P if the light is spherical or point light source. though when we want to account for indirect lighting, every surface above P may redirect light towards P. though, as we just mentioned. finding the direction of light rays when u deal with delta lights 很小的光源 is simple but how do we do that when light is emitted by a surface? 如果是一个表面就不是那么简单了。?
there is no unique point light position from which the light direction can be computed. in fact, since we deal with a surface, there is as an inifinity 无穷 of points we could chose on the surface of that object to compute the light direction. and why should we choose one direction rather than another considering that every point on the surface of that object is likely to reflect light towards P?

the answer to this question is both simple and difficult. in some very specific situations, the problem can be sovled analytically, there is a closed-form solution to this problem. in other words, it can be solved with an equation. this happens when the shapes of the objects making up the scene are simple (sphere, quads, rectangles), when the objects are not shadowing each other and when they have constant illumination across their surface.
as u can see this makes a lot of “if”. in other words, it is for example quite simple to compute the exchange of light energy between two rectangular patches or between a rectangle and a sphere as long as they are not occluded by some other objects and as long as they have a constant color. but as soon as we place a third object between the patch and the sphere or as soon as we shade these objects, then these simple analytical closed-form solutions do not work anymore. to find more information on this topic please check the lessons on rendering in the next sections (and especially the lesson on radiosity).

we thus need to find a more robust solution to this problem in which the solution works regardless of the obejcts shapes and does not depends on objects visibility. it turns out that solving this problem with these constraints限制 is pretty hard. hopefully we can use a simple method called Monte Carlo integration. the theory behind Monte Carlo integration is explained in great detail in two lessons u can find in the section The Mathematics of Computer Graphics. But why integration? because in essence what we are trying to do is “gather” all light coming from all possible directions above the hemisphere oriented about the normal at P and this in mathematics, can be done using what we call an “integral” operator:

Ω (the capital Greek letter for omega) here represents the hemisphere of directions oriented about the normal at P. it defines the region of space over which the integral is performed.

what we integrate is generally a function. so what is that function in our case? if u look at firgure 3, u can see the illumination of P by other objects in the scene, as a function.

figure 4: the amout of light reflected by objects in the scene towards PP the shading point, can be written as function of solid angle, which we can also re-write in terms of spherical coordinates. In the 2D case, it is just a function of the angle θθ. This is the function that we want to integrate over all directions contained in a half-disk in the 2D case and a hemisphere in 3D.

this function is non-zero in whatever parts of the half-disk onto which objects in the scene are projected to (assuming the objects themselves are not black). This function can be parametrised in different ways. It can be a function of solid angle (the Greek letter omega: ω) or a function of the spherical coordinates θ and ϕ (the Greek letters theta and phi). These are just two different ways (but equally valid) of parametrising the hemisphere. If we just consider the 2D case (figure 3), then this can simply be defined as function of the angle θ.

in this series of lessons on shading, we decided to avoid using terms from radiometry to make this introduction less technical. though, it may be interesting at this point of the lesson to introduce the concept of radiance which u will probably come across if u read other documents on global illumination. radiance is the term we should be using in this context to describe light reflected by objects in the scene towards P. it is often given the letter L.

If you are unfamiliar with the concept of integral, we really advice you to read the lessons from the Mathematics and Physics of Computer Graphics section. Though you can read or understand this sign as “collect the value that is to the right side of the integral sign (in this case LiLi) over the region of space ΩΩ (which again in this case, stands for the hemisphere oriented about NN, the shaded point normal, or the half-disk in the 2D case)”. imagine for example that “rice grains” are actually spread across the surface of that hemisphere. the integral simply means “collect or count the number of grains that are spread over the surface of that hemisphere”. though note that “rice grains” are discrete elements. it is easy to count them but in our case, what we want is to measure the amount of light reflected by the surface of objects which are directly visible from P. this is a far more complex problem because these surfaces are continuous and can not be broken down into discrete elements like grains. but the principle stays the same.

u should start to see how we will solve the “which point on the surface of an object should we choose to compute the contribution of that object to the illumination of my shaded point P”. the fact that we use an integral here and need to gather all light coming from all directions. suggests that it is not one point on the surface of that we need but all the points making up the surface of that obejcts. of course trying to cover the surface of an object with points is not practical neither possible. points are singularities, i.e. they have no area thus we can not actually represent a surface with an infinity of points which have no physical size. to solve the problem, one possible solution would be to divide the surface of the object into a very large number of very small patches and compute how much each patch making the surface of that object contributes to the illumination of P. this, in computer graphics, is technically possible and is called the radiosity method. a methods exists to solve the problem of light transfer between small pathces and P but they have limitations (they are good for diffuse surfaces but not good for glossy or specular surfaces). more information on the radiosity method can be found in the next lesson. another method would consist of dividing the surface of the objects into small pathches and simulating the contribution of these patches to the illumination of P by replacing them with small point light sources. this would somehow be possible and an advanced rendering technique called VPL is based on this exact principle, but in the end monte carlo ray-tracing is just simplier and more generic.

Monte Carlo is another way of solving the problem. It is essentially a statistical method that is based on the idea that you can approximate or estimate how much light is redirected towards PP by other objects in the scene, by casting rays from PP in random directions above the surface and evaluating the color of the objects these rays intersect (if they do intersect geometry). The contribution of each one of these rays is then summed up and the resulting sum is divided by the total number of rays. In pseudo-mathematical terms, you can write:

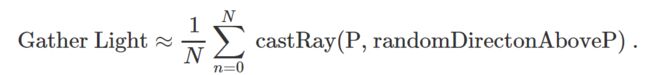
this is quick note for readers who are already familar with the concept of monte carlo integration. u probably already know that the complete equation to compute an approximation of an integral using monte carlo integration is:

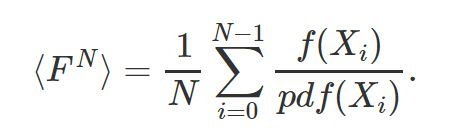
If you are not familiar with Monte Carlo methods, you can find them explained in two lessons from the section Mathematics of Computer Graphics. If you look at the equation above, you will notice a PDF term which we will ignore for now, just for the sake of simplicity. We just want you to understand the principle of Monte Carlo integration at this point, so don’t worry too much about the technical details which we will study in the next chapter.

The easiest way of making sense of the Monte Carlo integration method if you have never heard about it before, is to think of it in terms of polls. Let’s say you want to know the average height of the entire adult population of a country. You can measure the height of each person, sum up all the heights and divide this sum by the total number of people. Though of course, in general there is too many people in this population and it would take too long to do so. We say the problem is intractable. What you do instead is measure the height of a small sample of that population, sum up the numbers and divide the sum by the sample size (let’s call this number N). The technique works if people making up that sample are chosen randomly and with equiprobability (each individual making up the sample has the same chance to be part of the sample than any other individual making up the population). This is what we call a poll. The result that you get is probably not the exact number, but is generally a “good” estimation of that number. Increasing N, increases (in terms of probability) the quality of your estimation. The principle is exactly the same for approximating or estimating the amount of light reflected towards PP by other objects in the scene. The problem is also intractable because we can’t account for all the directions contained in the hemisphere (as mentioned before, surfaces are continuous and there’s an infinity of points on their surface and therefore an infinity of directions, thus the problem is intractable here as well). Therefore we just select a few directions which we choose randomly and take the average of their contribution.
Which in pseudo-code translates to:

Which in pseudo-code translates to:

In CG, we call these random directions samples. What we actually do with Monte Carlo sampling is sampling or taking samples over the domain of the integral or the region of space over which the integral ∫ΩLi∫ΩLi is performed, which in this particular case is the hemisphere.

Now, don’t worry yet about how we choose these random directions over the hemisphere and how many samples N we need to use. We will provide more information on this soon. For now what you need to remember from this part of the lesson, is that the Monte Carlo integration method only provides you with an estimation (or approximation) of the real solution which is the result of the integral ∫ΩLi∫ΩLi. The “quality” of this approximation mostly depends on N, the number of samples used. The higher N, the more likely you are to get a result close to the actual result of this integral. We will come back on this topic in the next chapter.

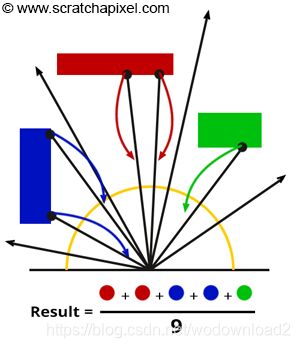
Figure 5: computing indirect illumination using the Monte Carlo integration method.
what do we mean by sampling? since we need to account for the fact that light can come from anywhere above P, what we do instead in the case of monte carlo integration, is to select some random directions within the hemisphere oriented about P and trace rays in these directions into the scene. if these rays intersect some geometry in the scene, we then compute the object color at the intersected point which we assume to be the amount of light that the intersected object reflects towards PP along the direction defined by the ray:

Vec3f indirectLight = 0; 
int someNumberOfRays = 32; 
for (int i = 0; i < someNumberOfRays; ++i) { 
    Vec3f randomDirection = getRandomDirectionHemisphere(N); 
    indirectLight += castRay(P, randomDirection ); 
} 
indirectLight /= someNumberOfRays;

Remember that what we want, is to collect all light reflected towards PP by objects in the scene, which we can write with the integral formulation: ∫ΩLi∫ΩLi. The variable ΩΩ here, represents the hemisphere of directions oriented around the normal at PP. This is the equation we are trying to solve and to get an approximation of this integral using Monte Carlo integration, we need to “sample” the function on the right side of the integral sign (the ∫∫ symbol), the LiLi term.

Sampling means take random directions from the domain of the integral we are trying to solve and evaluate the function on the right side of the integral sign at these random directions. In the case of indirect lighting, the domain of integral or the region of space over which the integral is performed, is the hemisphere of directions Ω.

Let’s now see how this work with an example. For now we will work in 2D but later in the lesson we will provide the code to apply this technique to 3D.
Let’s imaging that we want to compute the amount of light arriving indirectly at PP. We first draw an ideal half disk above PP and aligned along the surface normal at the shaded point. This half disk is just a visual representation of the set of direction over which we need to collect light reflected towards PP by surfaces in the scene. Next, we will compute N random directions which you can see a N points located on the outer line of the half-disk whose locations on that line are randomly selected. In 2D, this can be done with the following code:

step 1: what we do is first select a random location in the half disk of the unit circle which we can do by simply drawing a random value for the angle θθ anywhere in the range [0,π][0,π]. Computing a random angle can simply be done using some C++ random function (such as drand48()) which, if it returns a random float in the range [0,1][0,1], needs to be properly remapped to the range [0,π].