UVa - 10099 The Tourist Guide 并查集+贪心
【问题描述】
Mr.he有一家旅游公司。他得当前任务是带一些游客去一个遥远的城市。一些城市之间有双向道路。每对相邻城市之间都有一条高速公路,每条路线规定了自己的最大乘客数目。Mr.he有一份包含城市间道路的状况和公交车最大载重容量的地图。(最多有50000个城市,有100000条道路,道路的容量位于区间[1,100000]),并保证任意两点之间能相互到达。往往无法一次性地将所有乘客带往目的地。例如:在线面7个城市的地图中,边代表道路,每条边上的数字代表这条道路上公交车的最大载客量。
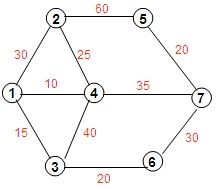
如果Mr.he要把99位乘客从城市1带到城市7,则至少要往返5次(他必须陪同每一群游客)。最佳路线是1-2-4-7。
帮助Mr.he找出所有游客带到目的地,且往返次数最少的路线,如果不能把游客送到目的地,输出“No”。
【输入格式】
第一行两个整数N和R,分别表示城市数量和道路数量,各城市编号为1..N。
接下来的R行,每行3个整数:A B P,表示道路AB的最大载客量为P。
最后有若干行,每包含3个整数:S D T,分别表示出发城市,目标城市的编号和游客数量,以0 0为结束。
【输出格式】
针对每个出发城市和目标城市,输出一个整数,表示需要往返的次数。
【输入样例】
7 10
1 2 30
1 3 15
1 4 10
2 4 25
2 5 60
3 4 40
3 6 20
4 7 35
5 7 20
6 7 30
1 7 99
3 7 70
0 0【输出样例】
5
3 【数据范围】
最多有50000个城市,有100000条道路,道路的容量位于区间[1,100000]
注:该题取自学校OJ,与UVa原题的输出格式有差异。
思路:将输入数据定义为结构体,先按数据的权值由大到小排序。(贪心思想)由大到小遍历每一条边时,用并查集的方法将已遍历的边并在一起。遍历一条边check一次是否已经出现可以从S到T的道路。若已出现,check前最后一次遍历的边即为最大载客量(注意将导游本身减去)。
/*
Name:The_Tourist_Guide
Copyright: Twitter & Instagram @stevebieberjr
Author: @stevebieberjr
Date: 11-07-16 13:59
*/
#include