方差分析(1) ——单因素方差分析及Excel示例

---

什么是方差分析

Wikipedia:
Analysis of variance (ANOVA) is a collection of statistical models used to analyze the differences among group means and their associated procedures (such as “variation” among and between groups), developed by statistician and evolutionary biologist Ronald Fisher.

方差分析（Analysis of variance，简称ANOVA，又称变异系数分析）是一类用于分析多组数据之间均值差异的统计方法模型，还涉及一些相关的步骤（比如两组数据之间的“变异”）。

---

从定义上看，方差分析是分析数据间均值的差异，那为什么叫“方差”分析，而不是“均值分析”？这是因为关于均值差异的结果是通过分析方差推算的，所以前者更合适。下面的具体步骤也将说明这一点。

这里仅对单因子方差方差分析¹(one-way ANOVA)假设检验的基本步骤进行说明。

建立假设

设单因子$A$有$r$个水平，记为$A_1,A_2,...,A_r$，不同水平($i$)下，各$m$次重复试验样本为$y_{ij}(i=1,2,...,r;j=1,2,...,m)$ ，每个水平可看作是一个总体，即水平$A_i$对应的$m$个观测样本集$\{y_{ij},j=1,2,....m\}$为一个总体，共$r$个总体。

假定，这里每个总体均为正态分布$N({\mu }_i,{\sigma }_i^2)$，各总体方差(${\sigma }_i^2$)相等，所有试验样本之间相互独立。 建立如下一对假设：
$$H_0:{\mu }_1={\mu }_2=...={\mu }_{r}vs{H}_1:{\mu }_1,{\mu }_2,...,{\mu }_r$$

若$H_0$成立，则说明因子$A$的$r$各水平间无显著差异，否则有显著差异。要检验原假设成立，即各总体均值相等，记总体均值为$\mu =({\sum }_{i=1}^{i=r}\mu )/r$，第$i$水平的均值与总体均值$\mu$的差$a_i={\mu }_i-\mu$作为$A_i$的水平效应，显然有$\sum a_i=0$，那原假设可看作是$H_0:a_1=a_2=...=a_r=0$，备择假设可看作是所以$a_i$不全为0。接着将给出检验$H_0$的统计量。

选择检验统计量

我们将通过偏差平方和建立检验统计量(F统计量)来对原假设($H_0$)进行检验。

首先，给出如下数据表：

因子水平	重复1	重复2	…	重复m		和	平均
$A_1$	$y_{11}$	$y_{12}$	…	$y_{1m}$		$T_1$	${\bar{y}}_{1\cdot }$
$A_2$	$y_{21}$	$y_{22}$	…	$y_{2m}$		$T_2$	${\bar{y}}_{2\cdot }$
…	…	…	…	…		…	…
$A_r$	$y_{r1}$	$y_{r2}$	…	$y_{rm}$		$T_r$	${\bar{y}}_{r\cdot }$
						$T$	$\bar{y}$

其中，(令$i=1,2,\dots ,r，n=r\ast m$)
$$\begin{array}{rl}{T}_i& =y_{i1}+y_{i2}+\dots +y_{im},\\ {\bar{y}}_{i\cdot }& =T_i/m,\\ T& =T_1+T_2+\dots +T_r,\\ \bar{y}& =({\bar{y}}_1\cdot +{\bar{y}}_2\cdot +\dots +{\bar{y}}_r)/r\\ & =(T_1/m+T_2/m+\dots +T_r/m)/r\\ & =T/(r\ast m)\\ & =T/n.\end{array}$$

偏差平方和

一般在统计学中，$k$个数据$\{y_1,y_2,...,y_k\}$(记$\bar{y}$为该组数据的均值)，偏差平方和为$$Q=\sum _{i=1}^{i=k}(y_i-\bar{y}{)}^2,$$有时简称平方和。注意到，这$k$个偏差之和为$0$，即有如下恒等式：$$\sum _{i=1}^{k=1}(y_i-\bar{y})=0,$$ 这说明在$Q$中独立(线性无关)的偏差只有个$k-1$个， 在统计学中把$k-1$称为偏差平方和$Q$的自由度$df=k-1$。偏差平方和常用来度量一组数据的离散程度，对于上表中的数据，将计算如下几种偏差平方和：

• 总体偏差平方和$S_T$
  这$n$个数据之间的差异大小用总体偏差平方和$S_T$表示: $$S_T=\sum _{i=1}^{i=r}\sum _{j=1}^{j=m}(y_{ij}-\bar{y}{)}^2,$$自由度为$d{f}_T=n-1$，经推算可得：
  $$\begin{array}{r}{S}_T=\sum _{i=1}^{i=r}\sum _{j=1}^{j=m}{y}_{ij}^2-\frac{T^2}{n}.\end{array}$$

• 组内偏差平方和$S_e$
  仅由随机误差引起各水平(组)内部间的误差，可用组内偏差平方和表示，也称误差偏差平方和：$$S_e=\sum _{i=1}^{i=r}\sum _{j=1}^{j=m}(y_{ij}-{\bar{y}}_{i\cdot }{)}^2,$$ 自由度为$d{f}_e=r(m-1)=n-r$.

• 组间偏差平方和$S_A$
  组间除了随机误差，还有因子$A$各水平(各组)之间效应不同产生的差异，用组间偏差平方和表示（也称为因子$A$的偏差平方和): $$S_A=m\sum _{i=1}^{i=r}({\bar{y}}_{i\cdot }-\bar{y}{)}^2,$$自由度 $d{f}_A=r-1$，经推算可得：$$S_A=\frac{1}{m}\sum _{i=1}^r{T}_i^2-\frac{T^2}{n}$$

从上述几种偏差平方和的表示方式很容易得到：$$S_T=S_A+S_e,$$ 自由度为$d{f}_T=d{f}_A+d{f}_e$.

$F$检验统计量

根据上面偏差平方和的定义，样本均值间的差异可转化为样本偏差平方和的差异，那么要想知道各水平之间是否有差异，就可以通过组间差与组内偏差进行比较得出。（一般情况下，组间的样本多于组内样本，而样本越多偏差平方和也会越大）

• 若各水平间无差异，也就是各水平间只有随机误差，没有效应不同带来的误差，则组间偏差与组内偏差比较接近，也就是组间偏差与组内偏差的比值比较接近1；
• 若各水平间有差异，也就是各水平间除了随机误差，还有不同效应带来的误差，这时各水平间的误差大于组内误差，则组间偏差与组内偏差的比值会大于1。

那么这个比值达到什么水平，才认为两者之间有显著差异？也就是比值多大，才拒绝原假设？这需要选择一个合适的检验统计量。下面先引入均方的概念。

均方的定义为每个自由度上有多少个平方和，均方 $MS$表示为: $$MS=\frac{Q}{d{f}_Q},$$其中，$Q$为偏差平方和，$d{f}_Q$为对应偏差平方和的自由度。

由于均方的定义排除自由度不同所产生的干扰，这将有利于各组样本偏差平方和间的比较，所以将组间偏差平方和的均方与组内偏差平方和的均方的比值F作为检验$H_0$的统计量：
$$F=\frac{M{S}_A}{M{S}_e}=\frac{S_A/d{f}_A}{S_e/d{f}_e}$$
其中，$S_A,S_e$分别是组间偏差平方和与组内偏差平方和，$d{f}_A,d{f}_e$为对应的自由度。

给出拒绝域并做出判断

这里的检验统计量$F$就服从自由度为$d{f}_A$和$d{f}_e$的$F$分布，由于$F$的值越大，越倾向于拒绝原假设，因此该检验的拒绝域$W$为$$W=\{F\ge F_{1-\alpha }(d{f}_A,d{f}_e)\},$$ 其中，$\alpha$为显著性水平，一般取$0.05$，这里$F_{1-\alpha }(d{f}_A,d{f}_e)$通过$F$分布查表获得。也就是说，

• 若$F\ge F_{1-\alpha }(d{f}_A,d{f}_e)$，则因子$A$各组间有显著差异；
• 若$F<F_{1-\alpha }(d{f}_A,d{f}_e)$，则说明因子$A$各组间差异不显著。

该检验的$p$值通过$F$分布对应的密度函数得到:$$p=P(Y\ge F).$$

$p$值是利用样本观测值做出拒绝原假设的最小显著性水平，一般在实际中，若$p$值很小($p\le 0.001$)时，可做出拒绝原假设；若$p>0.05$时，接受原假设。当$\alpha$与$p$比较接近时，才比较$\alpha$和$p$。如果$\alpha \ge p$，则在显著性水平$\alpha$下拒绝$H_0$；否则，在显著水平$\alpha$下接受原假设。

---

关于数据的计算可使用统计分析工具，一般有SPSS, SAS等，当然还有一般人接触最多的Excel，下面是利用Excel中的分析工具进行单因子方差分析。

使用Excel进行方差分析

添加数据分析工具

若功能区已经显示有“数据分析”功能（如下图）可跳过下面三步

1. 选择“数据”-> 右键“数据工具”-> 选择“自定义快速访问工具栏”，选择后将弹出“Excel选项”窗口(也可通过其他方式打开)；
   
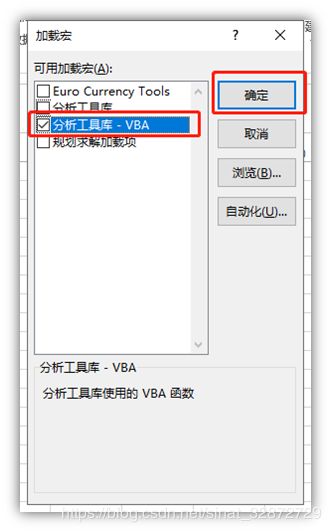
2. “Excel选项” -> “加载项” -> “分析工具库-VBA”-> “转到”，选择后会弹出“加载宏”的窗口
   
3. “加载宏”-> 在“分析工具库 - VBA”前打对勾 -> “确定”，此时Excel上的功能区就会显示“数据分析”工具(如最上面第一张图)
   

使用分析工具库

使用如下数据进行示例操作：

可根据上面方差分析的步骤直接计算，下面是使用Excel中的数据工具直接得到偏差平方和，自由度，均方等。

使用分析工具库进行单因子方差分析步骤：

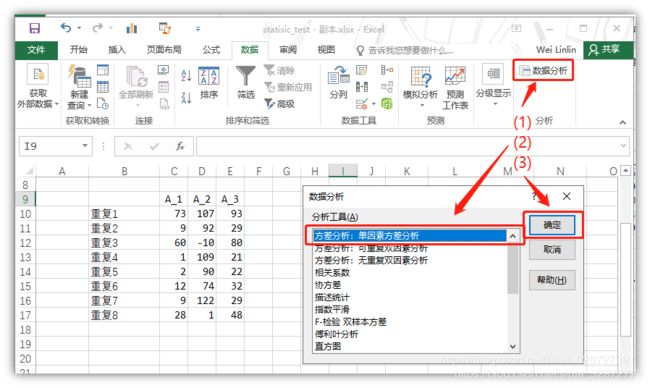
1. “数据分析”-> “方差分析：单因素方差分析”-> 点击“确定”后，会出现方差分析选项卡。这里请注意，Excel分析工具进行方差分析时，一列作为一组，所以将上面数据进行转置。
   

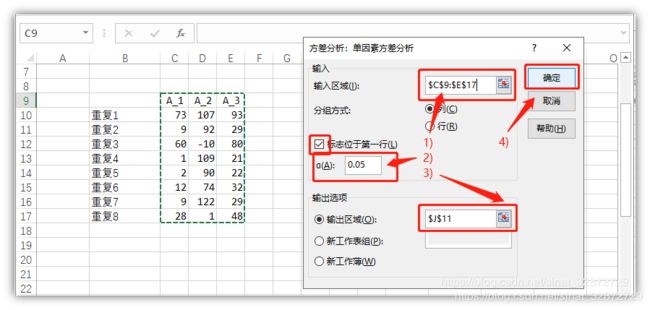
2. “方差分析：单因素方差分析”选项卡 -> 在“输入区域”选择要分析的数据(可通过右侧按钮鼠标选择，也可直接手动输入) -> 在“?(?)”的选择填显著性水平(默认0.05) -> 在“输出区域”选择输出单元格 -> 点击“确定”后，会计算出对应数据的结果，其中包含平方和(??) 、自由度(??)，均方(??) 等。(注：选项卡中"标志位于第一行"勾选表示 数据第一行为列名，在输出结果时会显示对应列名，若数据未选择列明则无需勾选，结果中列名会对应写成"列1", “列2”,…)
   

3. 点击确定后，就会直接给出该数据对应的方差分析表：
   

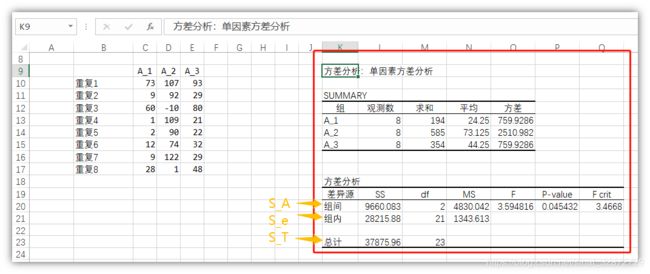
结果说明

结果中给出了两个汇总表：

• 第一个是各组数据之和，平均值，方差；
• 第二个是方差分析的结果表，其中
  - $SS$ 表示偏差平方和
  - $df$ 表示自由度
  - $MS$表示均方
  - $F$是对应组间和组内偏差平方和均方比值
  - $P$-$value$为对应$F$值的密度函数值，也可利用Excel中=F.DIST.RT(,<组间自由度>,<组内自由度>)$公式得到
  - $Fcrit$为对应$F$分布，$\alpha$置信水平下自由度为$d{f}_{组间}$和$d{f}_{组内}$的临界值，也可利用Excel中=F.INV(1-<\alpha>,<组间自由度>,<组内自由度>)公式得到

---

1. 茆师松,程依明, 濮晓龙.概率论与数理统计教程第二版[M].高等教育出版社:北京,2011:423-434. ↩︎