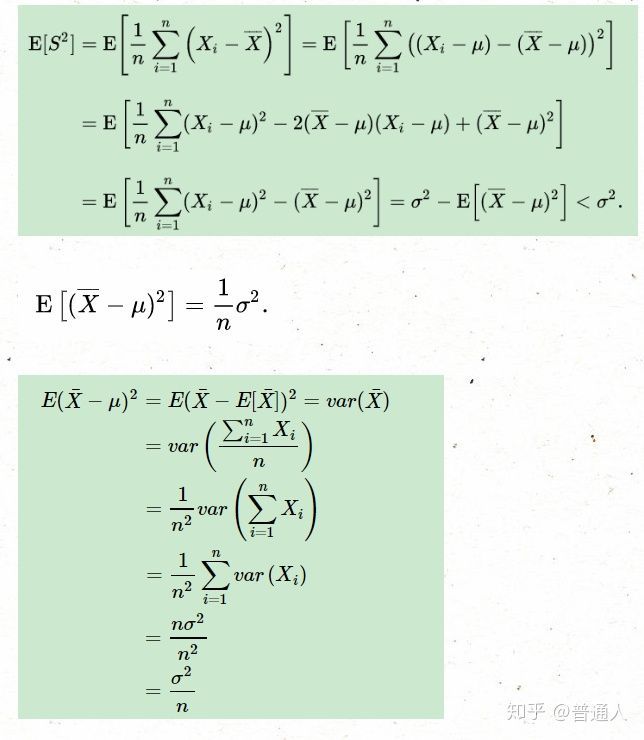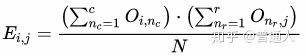卡方分布、方差分析
卡方分布:
首先我们先把现代数学中的数理统计中的卡方分布已经烂大街的定义先放下来,我先回到卡方检验的诞生的之地。
在1900年,皮尔森发表了著名的关于卡方检验的文章,该文章被认为是现代统计学的基石之一。在该文章中,皮尔森研究了拟合优度检验:……(这里之所以加点的原因是因为,下面的话很不好理解,我们举一个实际一点的例子就容易理解了。)
下面图片有个赌场的色子(注意阅读下面红色字体)
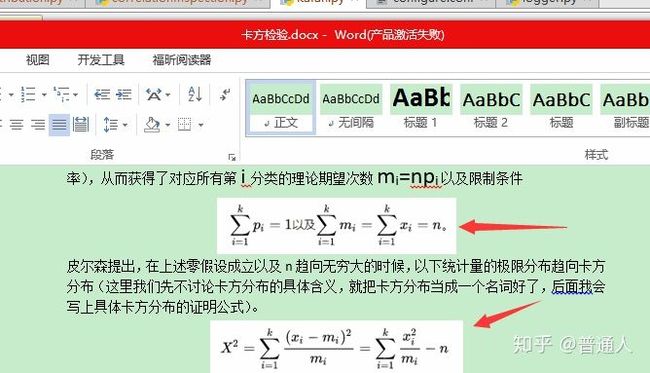
假设实验中从总体中随机取样得到的n个观察值(随机将色子抛n次)被划分为k个互斥的分类(分类为色子点数,1点2点3点4点5点6点),这样每个分类(每个点数)都有一个对应的实际观察次数Xi { i=1,2,...,k}。研究人员会对实验中各个观察值落入第 i个分类(色子在那个点数)的概率Pi的分布提出零假设(认为观测值与理论值的差异是由于随机误差所致,就是其概率是等于理论上的概率,相当于色子的频率等于我们理论得出概率),从而获得了对应所有第i分类的理论期望次数mi=npi以及限制条件
皮尔森提出,在上述零假设成立以及n趋向无穷大的时候,以下统计量的极限分布趋向卡方分布(这里我们先不讨论卡方分布的具体含义,就把卡方分布当成一个名词好了,后面我会写上具体卡方分布的证明公式)。
皮尔森首先讨论零假设中所有分类的理论期望次数mi均为足够大且已知的情况,同时假设各分类的实际观测次数xi均服从正态分布(这里可以参考中心极限定理)。皮尔森由此得到当样本容量n足够大时,上述表达式趋近服从自由度为k-1的卡方分布。
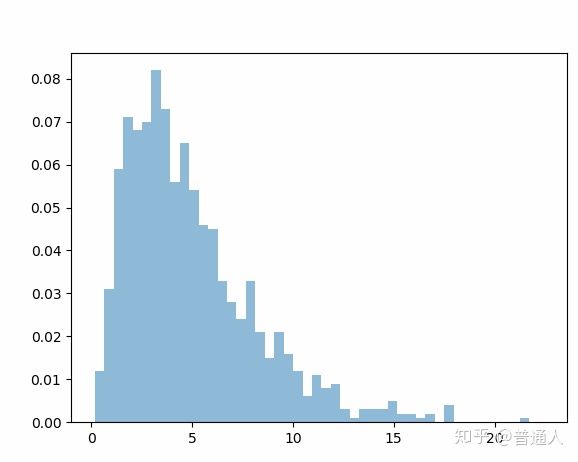
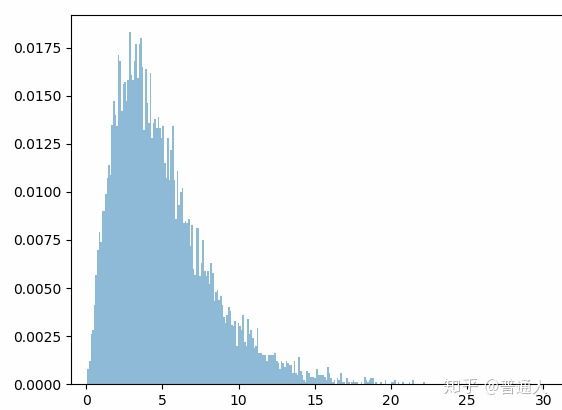
那好我们在没有证明的情况下先用计算机随机模拟一下,我们就用色子举例。
卡方样本按照对应类别的概率取1000次,这1000个取样随机分布在各个类别的频次按照以上公式得出单个卡方样本,之后取1000个卡方样本。
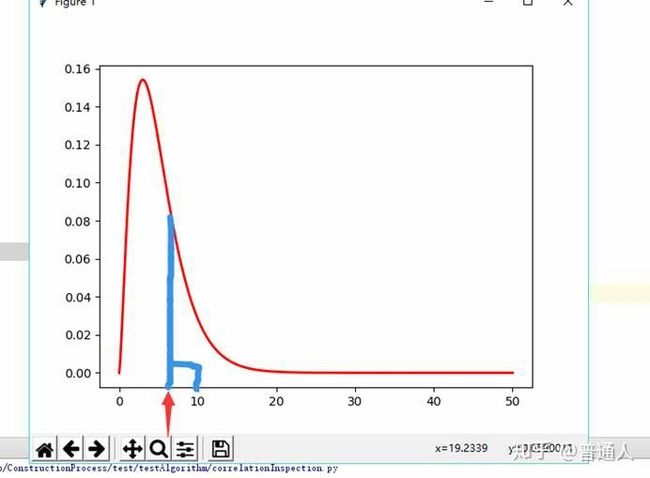
我们运行程序如下(为了大家方便清晰的看,我将代码就贴出来):
这个和卡方分布的概率密度曲线是不是很类似,参考代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import random
import copy
def getDatapInterval(datap):
'''
得到概率从小排到大的区间,便于按照概率取值
:param datap: k个类别的概率
:return:
'''
datapInterval = []
sump = 0
for x in datap:
sump = x + sump
datapInterval.append(sump)
return np.array(datapInterval)
def randomGenerated(datapInterval):
'''
依照概率分布区间随机取值
:param datapInterval:
:return:
'''
r=random.random()
for index, item in enumerate(datapInterval):
if r<=item:
return index
def samplingN(datapInterval,n):
'''
频次计数---初始化频次为0
:param datapInterval: 频率从小到大的区间
:param n: 取样次数
:return: 返回频率区间取样的频数
'''
frequencyCount = np.zeros(datapInterval.__len__())
for i in range(n):
index=randomGenerated(datapInterval)
frequencyCount[index]=frequencyCount[index]+1
return frequencyCount
def getSingleKaFan(datap,n):
'''
得到单个卡方分布
:param datap: 概率
:param n: 随机取样次数
:return:
'''
#得到概率区间
datapInterval=getDatapInterval(datap)
# 理论的概率频数为n*pi
theoryFrequencyCount = np.array(copy.deepcopy(datap))
theoryFrequencyCount = theoryFrequencyCount * n
#得到随机取样的频数
frequencyCount=samplingN(datapInterval,n)
x2=((frequencyCount - theoryFrequencyCount) ** 2)/theoryFrequencyCount
return np.sum(x2)
def getKaFanArrs(datap,n,arrn):
'''
取多少个卡方样本
:param datap: 概率
:param n: 单个卡方取样次数
:param arrn: 取多少个卡方样本
:return: 返回卡方样本数组
'''
kaFanArrs=[]
for i in range(arrn):
x2=getSingleKaFan(datap,n)
kaFanArrs.append(x2)
return np.array(kaFanArrs)
def draw_hist(limit_distribution):
'''
卡方检验的直方图绘制
:param limit_distribution: 分布数组
:return:
'''
minx=min(limit_distribution)
maxx=max(limit_distribution)
difference=maxx-minx
segmentation=difference/50
bins = np.arange(minx,maxx,segmentation) # 固定落区域
# 限制x轴范围
plt.xlim((-1,minx+difference))
#直接按照直方图频率显示,而不是频数
plt.hist(limit_distribution, bins=bins,weights=[1.0/ len(limit_distribution)] * len(limit_distribution), alpha=0.5)
#plt.plot(bins,chiSquareFunc(100,bins), linewidth=2, color='r')
plt.show()
#概率数据 分别为k个类别对应的概率---按照顺序进行排列 所以自由度为k-1
datap=np.array([1/6,1/6,1/6,1/6,1/6,1/6])
limit_distribution=getKaFanArrs(datap,1000,1000)
print(limit_distribution)
draw_hist(limit_distribution)
我们接下来要证明卡方分布公式:
详细的证明过程在另一篇博客中
http://www.zxheyi.cn/blog/toBlogPage.form?blogtitleID=133
(我这里只是提及几个关键点):
第一个是证明公式中用到的伽马函数:
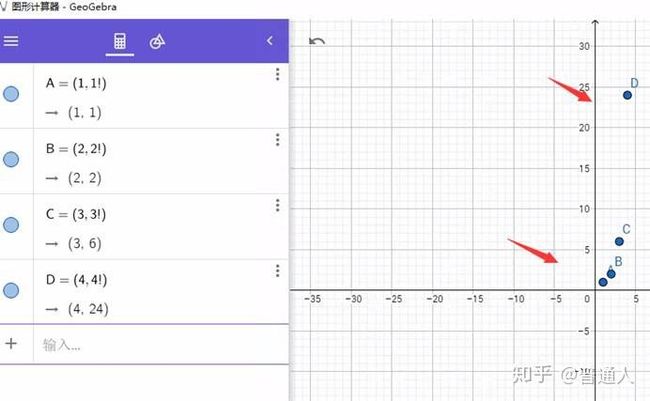
大家高中的时候都接触过阶乘像图片下面这样的阶乘,但是这个是不连续的。
而早期研究中心极限定理(那个时候的中心极限定理证明不是用的现代数学证明)的数学家斯特林得出了n!的近似值(这个时候的近似值还是基于整数)而之前研究数列牛顿插值公式来确定近似函数(如泰勒公式)数学家想能否用插值得出一个阶乘的近似函数,于是经过数学家的不懈努力最后确定了积分形式下的伽马函数将阶乘扩展到实数域上(说实话每当我去了解数学史时由衷的钦佩这些数学家)于是得出了大名鼎鼎的伽马函数。
第二个是证明自由度为1的卡方分布
第三个用卷积公式证明多个卡方样本连加下的结果
之后卡方分布概率密度的一般形式的公式就可以证明出来:
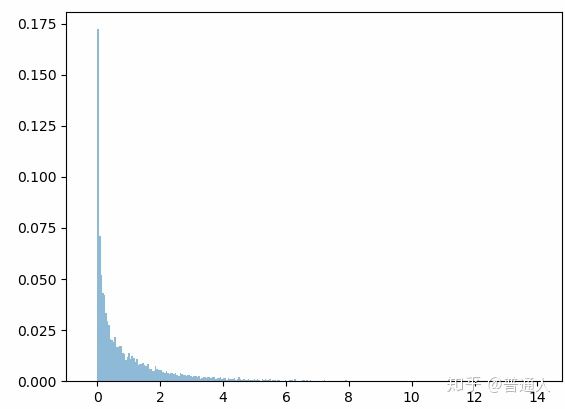
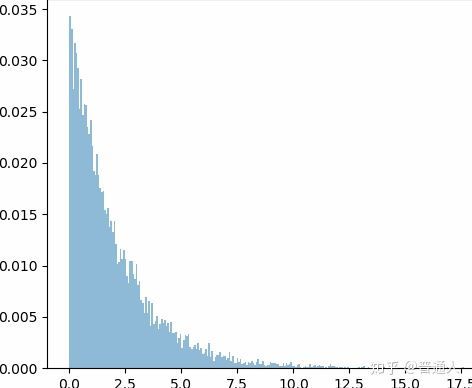
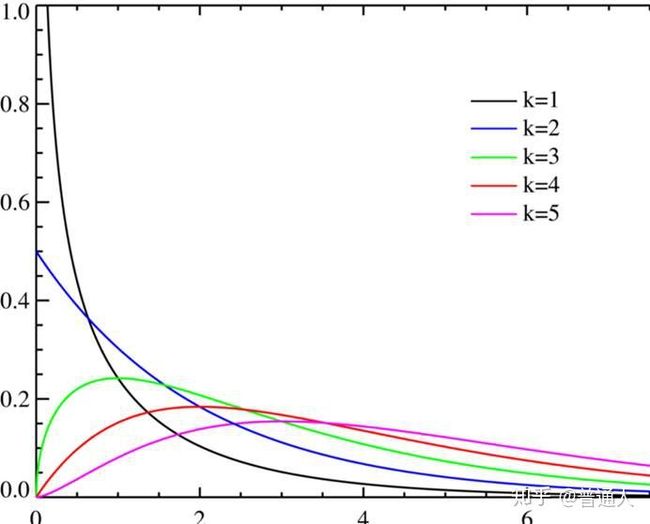
我们这里也可以随机模拟一下随机变量服从正态分布不同下的自由度卡方频率分布图。
自由度为1
自由度为2
自由度为5
很明显和概率论不同自由度下的密度曲线是很吻合的:
这里的自由度要理解的话可以参考无偏估计,其中方差的的无偏估计是最经典的,我这里只提及一下,有兴趣研究的可以深入查阅资料。
以上是方差的无偏估计。这也是为啥我们估计方差的时候要减去1/n个方差,所以方差的无偏估计自由度为n-1
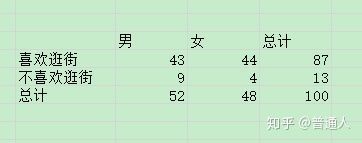
好了得到这个公式有什么用,之所以要摆出卡方概率密度函数是用来做假设检验的(我们后面再说),在数学中我们知道如果A,B两个事件独立那么P(AB)=P(A)*P(B),我们高中如果接触的是人教版的数学中,数学书中肯定有列联表这个东西。
如果相互独立那理论上可以得出P(男同时喜欢逛街)如下:
P(男)=52/87 P(喜欢逛街)=87/100
P(男同时喜欢逛街)= P(男)* P(喜欢逛街)
如果列联表共有 r 行 c 列,那么在独立事件的假设下,每个字段的“理论次数”(或期望次数)为:
我们之前在文章中是提出了一下两个公式的
所以(参考维基百科上如下得出了一个卡方的统计值)
自由度=(r-1)(c-1)
那我们有了卡方分布的概率密度曲线可以用来假设检验了,如下图我们知道概率是概率密度曲线下的面积(积分计算)我们画线的地方也就是卡方分布的随机变量小于等于这条线的概率为95%,如果你的卡方随机变量超过了这条线发生的概率为小概率事件,我们可以假定为不可能事件。
我们计算机模拟计算一下(代码如下):
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import random
from copy import deepcopy
import scipy as sy
from scipy.stats import chi2 #导入卡方分布常见需要的包
from scipy.stats import norm
from scipy import integrate #某些包需要单独的导入
from sympy.integrals.transforms import mellin_transform
from sympy import exp
from sympy.abc import x, s
from scipy.special import gamma
#数学带符号运算库---考虑性能暂时不启用
#import sympy as smy
def fxNormal(x,sigma,mu):
'''
正态分布的密度函数
:param x: 随机变量
:param sigma: 标准差
:param mu: 均值
:return: 返回正态分布的密度函数计算过的值(区间上的积分才是概率)
'''
left=1 / (sigma * np.sqrt(2 * np.pi))
right=np.exp(- (x - mu) ** 2 / (2 * sigma ** 2))
result=left*right
return result;
def getNormalXY(xmin,xmax,step ,sigma,mu):
'''
分布调用函数
x,y=getNormalXY(-100,100,0.01,1,0)
plt.xlim(-2,2)
plt.plot(x,y);
plt.show()
:param xmin: 最小的x值
:param xmax: 最大的x值
:param step: 描点分割
:param sigma: 标准差
:param mu: 均值
:return: 返回区间描点的图
'''
x = np.arange(xmin, xmax, step);
y = []
for xi in x:
y.append(fxNormal(xi,sigma,mu))
return x,y
def drawDistribution():
'''
标准化分布的检验
:return:
'''
mu, sigma = 0, 1 # mean and standard deviation
#产生正态分布的随机数 r = norm.rvs(size=1000) 等同
s = np.random.normal(mu, sigma, 10000)
#和标准正态分布的均值比较
print(abs(mu - np.mean(s)))
#和正态分布的标准差做比较---这里ddof表示的是自由度
print(abs(sigma - np.std(s, ddof=1)))
#得到计数,区间
count, bins, ignored = plt.hist(s, 30, normed=True)
plt.plot(bins,fxNormal(bins,sigma,mu),linewidth=2, color='r')
plt.show()
def takeArrayValue(arr,n):
'''
随机放回抽样拿取数组n次
:param arr: 抽样数据的数组
:param n: 次数
:return: 返回抽样好的数组
'''
max=arr.__len__()-1;
resultArr=[]
while n>0:
index=random.randint(0,max)
resultArr.append(arr[index])
n=n-1
return resultArr
def chiSquareDistribution(chiSquareNum,n):
'''
生成卡方分布
:param chiSquareNum: 生成卡方随机数个数
:param n: 卡方分布随机数n值
:return: 返回生成卡方分布随机的大小
'''
chiSquareDisArr=[]
for i in range(chiSquareNum):
# 产生正态分布的随机数
randomNormalArr = np.random.normal(0, 1, n)
#将卡方值加入数组
chiSquareDisArr.append(np.sum(randomNormalArr*randomNormalArr))
return chiSquareDisArr
def draw_hist(limit_distribution):
'''
卡方检验的直方图绘制
:param limit_distribution: 分布数组
:return:
'''
minx=min(limit_distribution)
print(minx)
maxx=max(limit_distribution)
difference=maxx-minx
segmentation=difference/300
bins = np.arange(minx,maxx,segmentation) # 固定落区域
# 限制x轴范围
plt.xlim((-1,minx+difference))
#直接按照直方图频率显示,而不是频数
plt.hist(limit_distribution, bins=bins,weights=[1.0/ len(limit_distribution)] * len(limit_distribution), alpha=0.5)
#plt.plot(bins,chiSquareFunc(100,bins), linewidth=2, color='r')
plt.show()
# def gammaIntegral(s):
# '''
# 计算伽马函数积分值
# :param s: 伽马含参量变量
# :param integralCeiling: 积分上限
# :return:
# '''
# # # 第一种计算伽马函数办法
# # gama = lambda x: sy.exp(-x) * sy.power(x, s - 1)
# # print(integrate.quad(gama, 0, sy.inf))#返回积分值 返回误差
# # #第二种计算伽马函数的办法
# # print(mellin_transform(exp(-x), x, s))
# #第三种直接调用伽马函数库
# #gamma(5)
# result=mellin_transform(exp(-x), x, s)
# return result[0]
# def chiSquareFunc(n,y):
# '''
# 卡方分布的概率密度函数
# :param n: 自由度
# :param y: 函数变量值数组
# :return: 返回概率密度计算的具体值按传入变量数组计算
# '''
# result = 0
# if y > 0:
# #result =1/ (sy.power(2, n / 2) * gamma(n / 2))* sy.power(y, n / 2 - 1) * sy.exp(-y / 2)
# #等同于调用一下函数---chi2.pdf(0.01,1)
# result =1 / (np.power(2,n/2)*gamma(n/2)) * (y)**(n/2-1) * exp(-y/2)
# return result
# print(chi2.pdf(0.01,1))
def draw_chi(n):
'''
卡方分布曲线图
:param n:
:return:
'''
chiarr=np.linspace(0,50,1000)
plt.plot(chiarr, chi2.pdf(chiarr,n), linewidth=2, color='r')
plt.show()
def chiSquareDistTest(n):
'''
测试方法,用来测试卡方频率分布的,得到卡方图
:param n: 自由度
:return:
'''
limit_distribution=chiSquareDistribution(10000,n)
draw_hist(limit_distribution)
if __name__ == '__main__':
#绘制卡方分布密度曲线
#draw_chi(1)
#绘制卡方分布概率频率图
#chiSquareDistTest(5)
#cdf(x, df, loc=0, scale=1)
#计算分位点
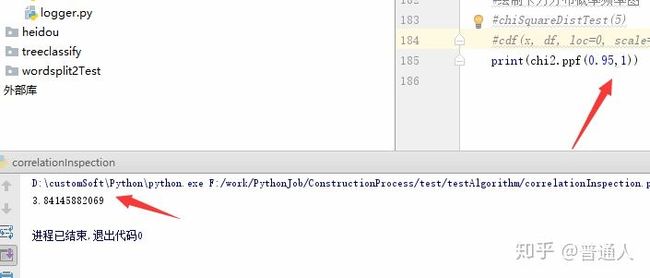
print(chi2.ppf(0.95,1))
可以看到自由度为1时的分位点为3.84145882069
而计算的卡方值为1.77,我们有充分理由无法说明这个两个类别不相互独立。
所以卡方检验在数理统计中占有及其重要的作用,接下来我们还会用到这个写另外几篇单身狗系列。
参考文章:
(皮尔森卡方检验)
http://www.flickering.cn/%E6%95%B0%E5%AD%A6%E4%B9%8B%E7%BE%8E/2014/06/%E7%A5%9E%E5%A5%87%E7%9A%84%E4%BC%BD%E7%8E%9B%E5%87%BD%E6%95%B0%E4%B8%8A/
(卡方检验)
https://zh.wikipedia.org/wiki/卡方检验
(神奇的伽马函数)
http://www.flickering.cn/%E6%95%B0%E5%AD%A6%E4%B9%8B%E7%BE%8E/2014/06/%E7%A5%9E%E5%A5%87%E7%9A%84%E4%B
方差分析:
即使是没学过统计学,没分析过数据的人,我想如果让他们说出三个最常听到的分析方法,方差分析一定位列其中。系统介绍方差分析的文章其实已有很多,从网上随便搜罗的教程就足够看上一整天。不过接下来,就让我们抛开那些复杂的公式,难理解的概念,站在一个更为实用的角度,重新认识它。
本文将从概念、数据格式、方差分析前提、操作步骤、结果分析、事后比较、其他指标说明,共7个部分进行说明。
01. 概念
方差分析用于定类数据(X)与定量数据(Y)之间的差异分析,例如研究三组学生(X)的智商平均值(Y)是否有显著差异。其中X的组别数量至少为2,也可以分析三个或三个以上组别的数据。
定类数据是指数字大小代表分类的数据(如1=男,2=女;1=第一组,2=第二组,3=第三组)
定量数据是指数字大小具有比较意义(如量表题:非常不满意,比较不满意,中立,比较满意,非常满意)
- 如果X为定类,Y为定量;且X分为两组,比如男和女;此时也可使用t检验进行差异对比。T检验与单因素方差分析的区别在于T检验只能对比两组数据的差异。
- 如果X和Y均为定类数据,想对比差异性,此时需要使用卡方分析。
02. 格式要求
在分析前首先需要按正确格式录入、上传才能得到有效的分析结果。针对方差分析,正确的录入格式如下图所示:
03. 方差分析的基本前提
进行方差分析需要数据满足以下两个基本前提:
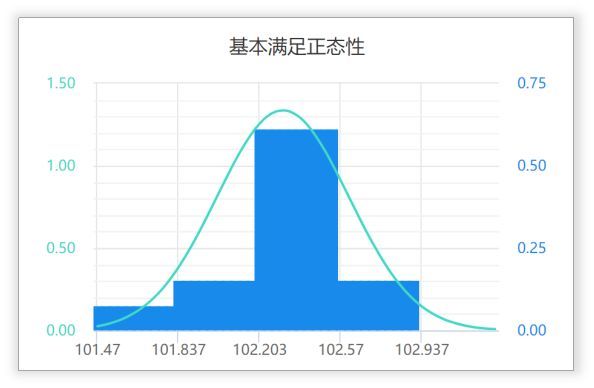
- 各观测变量总体要服从正态分布
- 各观测变量的总体满足方差齐
这是方差分析的两个基本前提条件,理论上讲,数据必须满足以上两个条件才能进行方差分析,如不满足,则使用非参数检验。
但现实研究中,数据多数情况下无法到达理想状态。正态性检验要求严格通常无法满足,实际研究中,若峰度绝对值小于10并且偏度绝对值小于3,或正态图基本上呈现出钟形,则说明数据虽然不是绝对正态,但基本可接受为正态分布,此时也可使用方差分析进行分析。
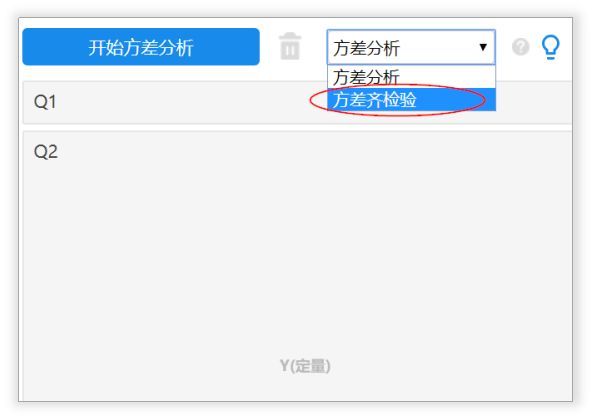
方差齐性检验是用于判断不同组别下的数据波动情况是否一致,即方差齐。若P值呈现出显著性(p <0.05)则说明,不同组别数据波动不一致,即说明方差不齐;反之p值没有呈现出显著性(p>0.05)则说明方差齐。
同样的,方差分析前也需要进行方差齐性检验,理论上数据进行方差齐检验没有呈现出明显显著性(即P>0.05),才可使用方差分析,但一般来讲如果不满足方差齐条件,检验性能也较好,因而多数时候并没有进行方差齐检验就直接使用方差分析(方差齐检验可在SPSSAU通用方法->方差中使用)。
04. 操作步骤
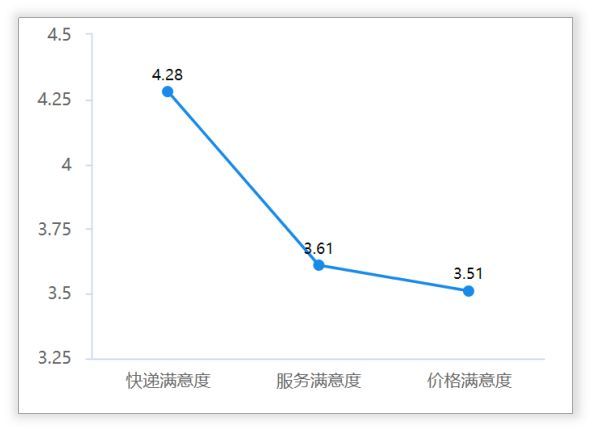
以上面“服务满意度”、“快递满意度”和“价格满意度”之间的差异比较为例,进行方差分析。
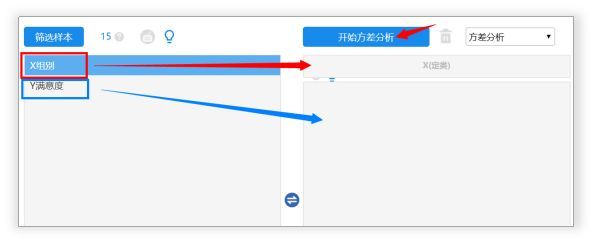
操作步骤如图所示:
将X组别放于上方分析框内,Y满意度放于下方分析框内,点击“开始方差分析”。
05. 结果分析
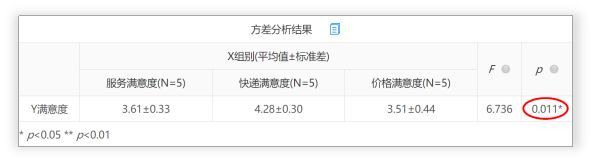
(1)首先关注P值,分析X与Y之间是否呈现出显著性。上表中可以看出,不同组别样本下的满意度均呈现出显著性(P<0.05),说明“服务满意度”、“快递满意度”和“价格满意度”之间确实存在差异性。
*备注:F值为计算过程值,用于计算P值,通常不需要单独对其进行分析。
(2)红线部分是每个分组下(X),满意度(Y)的平均值±标准差,用于在数据呈现出现显著性差异(P<0.05)后进一步了解差异情况。平均值呈现数据总体得分情况,标准差呈现数据波动情况。平均值±标准差即可代表数据总体特征。
此数据中,通过平均值得分对比发现,“快递满意度”相比“服务满意度”和“价格满意度”有较高的满意度,即“快递满意度>服务满意度;快递满意度>价格满意度”。
(3)同时系统会生成可视化图形,可根据需要选择图形类型(折线图、柱状图、条形图、雷达图)
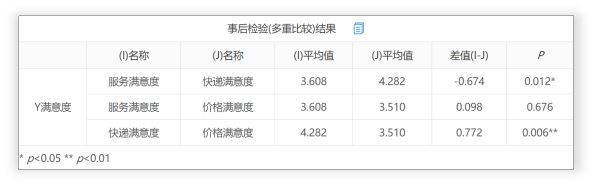
06. 事后多重比较
方差分析可用来多组数据的比较,如果不同水平下X对Y确实存在显著差异,此时还想进一步了解两两组别间数据的差异,该如何操作呢?
事后多重检验正是解决这一问题的方法。
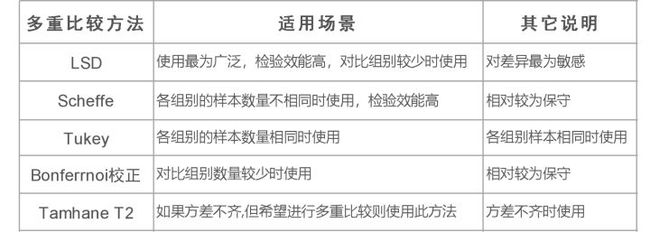
事后检验的方法有多种,但功能均一致,只是在个别点或使用场景上有小区别。SPSSAU目前共提供LSD,Scheffe,Tukey,Bonferroni校正,Tamhane T2常见的五种方法,其中LSD方法最常使用。
需要注意的是,事后多重比较是基于方差分析基础上进行的,因此首先要满足方差分析确实存在显著性差异,接着才来比较两两的差异。如果本身只有两组数据做比较或者方差分析显示P值大于0.05各个组别之间没有差异性,此时则不需要进行事后检验。
07. 其他常用指标
方差分析如果呈现出显著性差异(P<0.05),可通过平均值对比具体差异,同时还可使用效应量(Effect size)研究差异幅度大小。
偏Eta方表示效应量,偏Eta方值介于0~1之间,该值越大说明差异幅度越大,比如Eta方为0.1,即说明数据的差异有10%是来源于不同组别之间的差异,一般情况下Eta值非常小,通常只需报告该值即可,没有固定标准。