【题解】平板涂色（洛谷 P1283）

题目

题目描述

CE 数码公司开发了一种名为自动涂色机（APM）的产品。它能用预定的颜色给一块由不同尺寸且互不覆盖的矩形构成的平板涂色。

为了涂色，APM 需要使用一组刷子。每个刷子涂一种不同的颜色$C_i$。APM 拿起一把有颜色$C_i$的刷子，并给所有颜色为 $C_i$ 且符合下面限制的矩形涂色：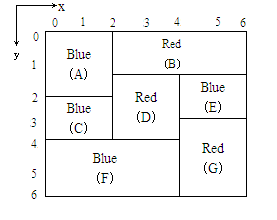
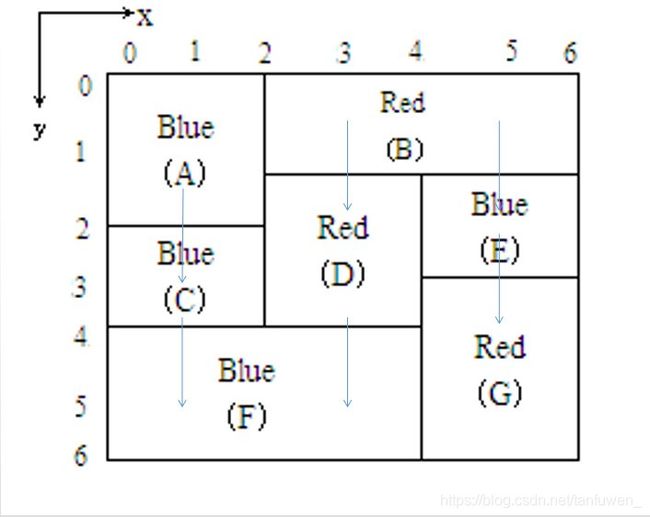
为了避免颜料渗漏使颜色混合，一个矩形只能在所有紧靠它上方的矩形涂色后，才能涂色。例如图中矩形 $F$ 必须在 $C$ 和 $D$ 涂色后才能涂色。注意，每一个矩形必须立刻涂满，不能只涂一部分。

写一个程序求一个使 APM 拿起刷子次数最少的涂色方案。注意，如果一把刷子被拿起超过一次，则每一次都必须记入总数中。

输入格式

第一行为矩形的个数 $N$。下面有 $N$ 行描述了 $N$ 个矩形。每个矩形有 $5$ 个整数描述，左上角的 $y$ 坐标和 $x$ 坐标，右下角的 $y$ 坐标和 $x$ 坐标，以及预定颜色。

平板的左上角坐标总是 $(0,0)$。

输出格式

一个整数，表示拿起刷子的最少次数。

输入输出样例

输入 #1

7
0 0 2 2 1
0 2 1 6 2
2 0 4 2 1
1 2 4 4 2
1 4 3 6 1
4 0 6 4 1
3 4 6 6 2

输出 #1

3

说明/提示

$1\le C_i\le 20$，$1\le N\le 16$。

题解

转化题目

首先我们需要把这个具体的图转化的抽象一点：

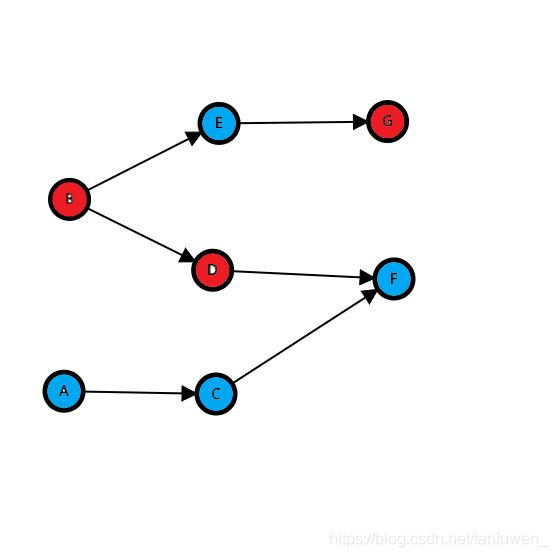
首先我们定义每一条有向边：边连接的是一上一下两个靠紧的矩形，如图

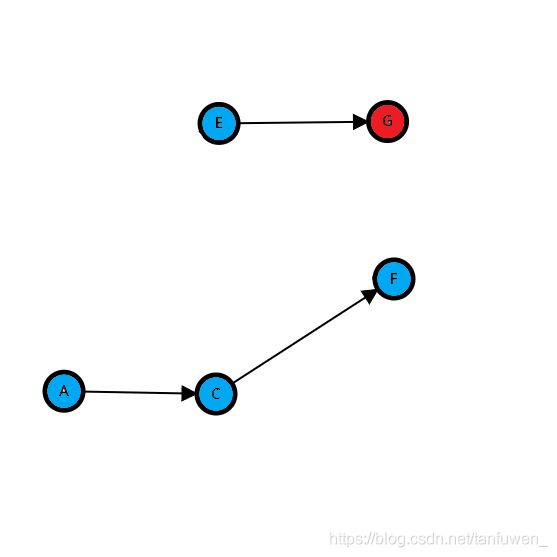
转化为更简洁的图就成为了

很明显对于每一个时刻，我们都只能为没有边指向它的节点上色。当然，上完色后，此节点及他的所有出边都将被删除（类似于拓扑排序）

现在我们跑一遍样例（不唯一）

首先我们换上红色的刷子，刷去B和D

再换上蓝色的刷子，刷掉A,C,F,E

最后换上红色的刷子，删去G

代码讲解

这么小的数据范围，有两个暗示：1.状压DP 2.暴力搜索

正解好像有DP,但是我不会＞﹏＜，所以在这里就讲讲暴力的DFS吧，减减枝也慢不到哪去

1.存图

首先是转化部分，即把原图转化为方便DFS跑的图

注意题目的一个坑点：

一个矩形只能在所有紧靠它上方的矩形涂色后，才能涂色

注意这个这个"紧靠"，划下来，要考

第一种情况：$Xa\_r>Xb\_l$

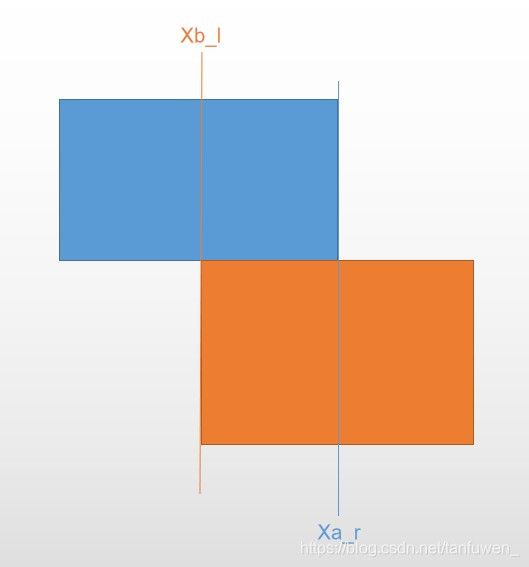
第二种情况：$Xa\_l<Xb\_r$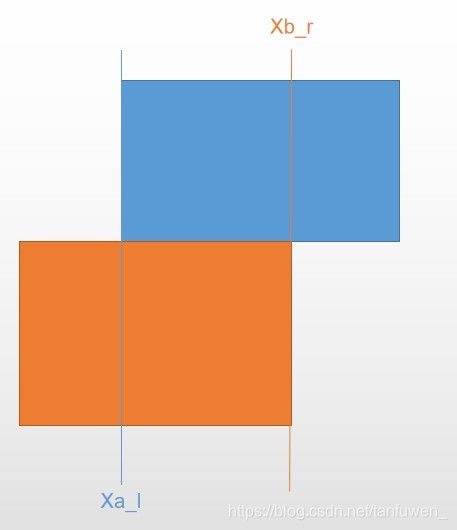
这两种情况都是需要在图中连边的（记为有先后关系）

为了后面的需要（判如图），我们需要反向连边，由下连到上

代码：

scanf("%d",&n);
for(int i=1;i<=n;i++){
	scanf("%d %d %d %d %d",&a[i].xa,&a[i].ya,&a[i].xb,&a[i].yb,&a[i].color);
}
int m=0;
for(int i=1;i<=n;i++){
	for(int j=1;j<=n;j++){
		if(i==j) continue;
		if(a[i].xa==a[j].xb && !(a[j].yb<a[i].ya || a[j].ya>a[i].yb)){
			g[i].push_back(j);
		}
	}
}

2.搜索

每次搜索有3个状态：目前的总拿刷子数，当前枚举完第几个节点，目前刷子的颜色（之前涂的颜色）

如果目前已经枚举完第n个节点，则直接让ans与目前的总拿刷子数取min

否则枚举每一个已经可以涂的节点（见下check），并搜索

dfs(sum+(last!=a[i].color),step+1,a[i].color);

这一步比较巧妙，特别是sum+(last!=a[i].color)

我们知道last为之前的颜色，与a[i].color相同则last!=a[i].color等于0，也就是目前的总拿刷子数不用加一，否则目前的总拿刷子数就需要加一

代码

void dfs(int sum,int step,int last){
	if(sum>=ans) return;
	if(step==n){
		ans=min(ans,sum);
		return;
	}
	for(int i=1;i<=n;i++){
		if(!vis[i] && (check(i) || !a[i].xa)){
			vis[i]=1;
			dfs(sum+(last!=a[i].color),step+1,a[i].color);
			vis[i]=0;
		}
	}
}

3.判断是否可涂

这就体现我们之前反向存图的重要性了，当一个节点的所有入度（反向后就是出度了）都被遍历，就可以认为这个节点已经可涂，但是算入度会不方便，所以我们反向存图，算出度就OK了

bool check(int u){
	for(int i=0;i<g[u].size();i++){
		if(!vis[g[u][i]]) return false;
	}
	return true;
}

完整代码

#include 
#include 
#include 
using namespace std;
const int MAXN=20;
struct node{ 
	int xa,xb,ya,yb;
	int color;
}a[MAXN];
vector<int> g[MAXN];
int ans;
bool vis[MAXN];
bool check(int u){
	for(int i=0;i<g[u].size();i++){
		if(!vis[g[u][i]]) return false;
	}
	return true;
}
int n;
void dfs(int sum,int step,int last){
	if(sum>=ans) return;
	if(step==n){
		ans=min(ans,sum);
		return;
	}
	for(int i=1;i<=n;i++){
		if(!vis[i] && (check(i) || !a[i].xa)){
			vis[i]=1;
			dfs(sum+(last!=a[i].color),step+1,a[i].color);
			vis[i]=0;
		}
	}
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d %d %d %d %d",&a[i].xa,&a[i].ya,&a[i].xb,&a[i].yb,&a[i].color);
	}
	int m=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i==j) continue;
			if(a[i].xa==a[j].xb && !(a[j].yb<a[i].ya || a[j].ya>a[i].yb)){
				g[i].push_back(j);
			}
		}
	}
//	for(int i=1;i<=n;i++){
//		printf("%d:",i);
//		for(int j=0;j
//			printf("%d ",g[i][j]);
//		}
//		cout<
//	}
	ans=0x3f3f3f3f;
	dfs(0,0,0);
	printf("%d",ans);
    return 0;
}

$The$ $end$