【算法专题】图论专题：并查集

并查集 是一种树型的数据结构，用于处理一些不相交集合的合并和查询问题。在使用中常常以森林来表示。

基本结构

并查集也是用来维护集合的，和前面学习的 set 不同之处在于，并查集能很方便地同时维护很多集 合。如果用 set 来维护会非常的麻烦。并查集的核心思想是记录每个结点的父亲结点是哪个结点。

• 初始化

void init() {    
 for (int i = 1; i <= n; ++i) {        
  fa[i] = i;     
  } 
  }

• 查找

int get(int x) {     
if (fa[x] == x) { 
// x 结点就是根结点         
return x;     
}   
return get(fa[x]); // 返回父结点的根结点 }

• 合并

void merge(int x, int y) {     
x = get(x);     
y = get(y);    
 if (x != y) { // 不在同一个集合       
   fa[y] = x;     
 }
 }

并查集实现

首先，我们把要用的变量初始化。

int fa[110]; 
int n, m;

我们先把并查集的框架实现好，便于后面直接调用。我们先实现初始化，用一个 init() 函数来实现初 始化。初始化实际上就是把每个点的父亲结点赋值为自己。

void init() {    
 for (int i = 1; i <= n; i++) {         
 fa[i] = i;     
 } 
 } 

接下来，我们继续实现get函数

int get(int x) {     
if (fa[x] == x) {         
return x;     
}     
return get(fa[x]); 
}

接下里我们实现 merge 函数，合并两个结点到一个集合。合并的方法很简单，先找到各自的根结点， 如果根结点不相同，让其中一个根结点的父亲变成另外一个根结点。

void merge(int x, int y) {    
 x = get(x);    
  y = get(y);    
   if (x != y) {         fa[y] = x;    
    } 
    }

这一步我们接收输入，在接收一组关系以后，我们通过 merge 合并他们到一个集合。注意，在这之 前，我们需要先初始化并查集。初始化要在 输入之后，这是平时写程序很容易错误的一个点。 在 main 函数里面写下

cin >> n >> m;
 init(); 
 for (int i = 0; i < m; i++) {     
 int a, b;    
 cin >> a >> b;     
 merge(a, b); 
 }

最后我们统计几何的个数。统计方法很简单，只需要统计集合的根结点的数量。

int cnt = 0; 
for (int i = 1; i <= n; i++) {    
 if (fa[i] == i) {        
  cnt++;    
   }
   } 
  cout << cnt << endl; 

最后，再来看一看运行一下，看一看结果。

6 4 1 2 2 3 1 3 4 5 

路径压缩

并查集的时间复杂度很高，最坏可以达到O（n），所以，我们更适用于路劲压缩的并查集，这一回，就来给大家讲一讲路劲压缩后的并查集。
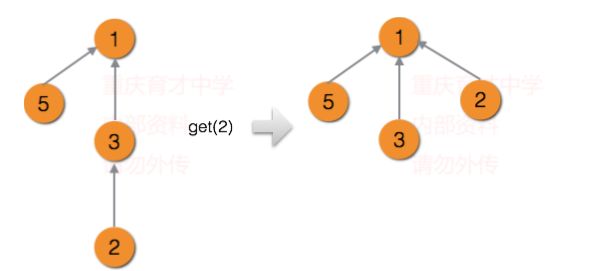
路径压缩 的思想是，我们只关心每个结点所在集合的根结点，而并不太关心树的真正的结构是怎么样 的。这样我们在一次查询的时候，可以直接把查询路径上的所有结点的 都赋值成为根结点。实现 这一步只需要在我们之前的查询函数上面进行很小的改动。

int get(int x) {     
if (fa[x] == x) { 
// x 结点就是根结点         
return x;     
}     
return fa[x] = get(fa[x]); // 返回父结点的根结点，并令当前结点父结点直接为根结点 
}

下面是进过比较的并查集（右图为路径压缩）

联通性

之前我们判断无向图的连通性的时候（有向图的连通性我们会在之后的课程介绍），用的是 DFS 的方 法。而用并查集来判断无向图的连通性，只需要把每一条边连接的两个点合并到一个集合就可以了，都 不必存图，最后如果集合个数为 ，说明整个图是连通的。

路径压缩的实现

#include  
using namespace std; 
int fa[110];
 int n, m; 
 void init() {    
  for (int i = 1; i <= n; i++) {        
   fa[i] = i;     
   } 
   } i
   nt get(int x) {    
    if (fa[x] == x) {        
     return x;    
      }     
      return get(fa[x]); 
      } 
      void merge(int x, int y) {    
       x = get(x);     
       y = get(y);    
        if (x != y) {        
         fa[y] = x;     
         } 
         } 
         int main() {     
         cin >> n >> m;     
         init();     
         for (int i = 0; i < m; i++) {        
          int a, b;         
          cin >> a >> b;        
           merge(a, b);     
           }     
           int cnt = 0;    
            for (int i = 1; i <= n; i++) {         
            if (fa[i] == i) {             
            cnt++;         
            }    
             }     
             cout << cnt << endl;     
             return 0;
              }

看一看结果

6 4 1 2 2 3 1 3 4 5

种类并查集

种类并查集是借助借助并查集来解决一系列种类查询问题。
问题描述如下，有 个人，我们不知道每个人的性别，但是有 组关系，每一组关系表示 和 是同 性或者异性，问这 组关系是否有矛盾。
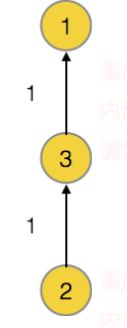
这个问题，可以二分图判定来做，这里我们学习带权并查集的解法。每个点的权值我们规定只用 和 两个值，用 表示这个点和父结点同性，用 表示这个点和父结点是异性。那么在查询的时候，我们 之需要把权值对 取模。比如 和 异性， 和 异性，那么 和 同性。

int get(int x) {     
if (fa[x] == x) {        
 return x;     
 }    
  int y = fa[x];    
   fa[x] = get(y);     
   dist[x] = (dist[x] + dist[y]) % 2;     
   return fa[x];
 }

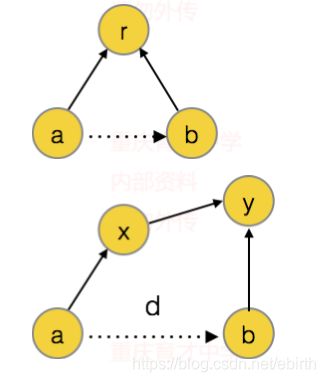
我们知道 和 的关系和 和 的关系，就可以计算出 和 的关系等于 和 和关系减去 和 的 关系，也就是 。
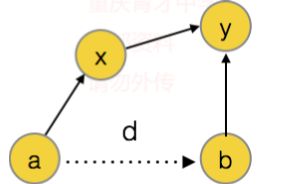
而如果 和 不属于同一个集合，说明他们之前的关系，假设他们现在的关系为 。这时候，我们合并 他们，这时候他们的关系如下图。

void merge(int a, int b, int d) {     
int x = get(a);    
int y = get(b);     i
f (x == y) {        
 // 同一集合，已知关系         
 if ((dist[a] - dist[b] + 2) % 2 != d) {             
 // 加上 2 再对 2 取模防止出现负数             
 cout << "No" << endl;        
  }     
  } else {        
   // 未知关系         
   fa[x] = y;         
   dist[x] = (dist[b] - dist[a] + d + 2) % 2;   
   } 
   }

多种关系种类并查集

用 表示和父结点平手， 表示战胜父结点， 表示被父结点战胜。这时候权值应该对 取模。而合并的时候权值的关系还是参考之前的两个图。