快速沃尔什变换（FWT）

问题

FWT用来解决这样的一个问题：
给出多项式A(x),B(x)，求C(x)，其中
C(k)=∑i⊕j=kA(i)B(j) C ( k ) = ∑ i ⊕ j = k A ( i ) B ( j )
（也可以换成and/or）
要求在 O(nlogn) O ( n log ⁡ n ) 的复杂度内求出C(x)

定义

定义 tf(A) t f ( A ) 操作表示（A是一个长度为2的幂的多项式，k表示A的长度，A0A1分别表示A的左半边和右半边）
则
tf(A)={A(tf(A0)+tf(A1),tf(A0)−tf(A1))k=1else t f ( A ) = { A k=1 ( t f ( A 0 ) + t f ( A 1 ) , t f ( A 0 ) − t f ( A 1 ) ) else
其中”,”表示物理顺序拼接

性质

然后有一条性质 tf(A)+tf(B)=tf(A+B) t f ( A ) + t f ( B ) = t f ( A + B )
证明略，可以用数学归纳法来证

因为C=A⊕B，所以可以得出 C=(A0⊕B0+A1⊕B1,A0⊕B1+A1⊕B0) C = ( A 0 ⊕ B 0 + A 1 ⊕ B 1 , A 0 ⊕ B 1 + A 1 ⊕ B 0 )
等于把异或第一位为0的数加到左边，异或第一位为1的数加到右边

然后xjb证出tf(A)tf(B)=tf(C) （当C=A⊕B时）
所以可以先求出tf(A)和tf(B)，之后相乘求逆

逆运算

定义tf(A)的逆运算utf(A)，表示utf(tf(A))=A
则
utf(A)={A(utf(A0)+utf(A1)2,utf(A0)−utf(A1)2)k=1else u t f ( A ) = { A k=1 ( u t f ( A 0 ) + u t f ( A 1 ) 2 , u t f ( A 0 ) − u t f ( A 1 ) 2 ) else
证明还是数学归纳法

所以这样对tf(C)做utf操作，就可以得出C了
而tf和utf操作都是 O(nlogn) O ( n log ⁡ n ) 的

其它

关于三种运算的tf和utf

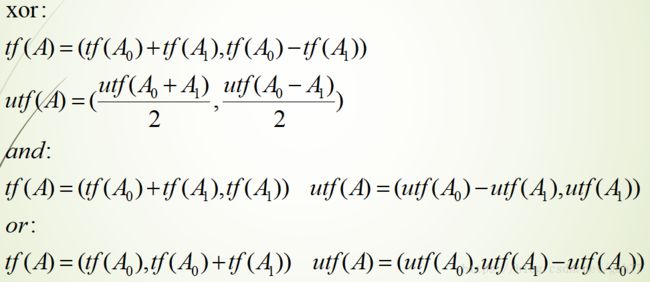
其中异或的utf是可以拆的，也就是说utf(A)+utf(B)=utf(A+B)
证明和tf基本一样（就是多了个/2）

例题

codeforces662CBinary Table 二进制表
C. Binary Table
time limit per test6 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
You are given a table consisting of n rows and m columns. Each cell of the table contains either 0 or 1. In one move, you are allowed to pick any row or any column and invert all values, that is, replace 0 by 1 and vice versa.

What is the minimum number of cells with value 1 you can get after applying some number of operations?

Input
The first line of the input contains two integers n and m (1 ≤ n ≤ 20, 1 ≤ m ≤ 100 000) — the number of rows and the number of columns, respectively.

Then n lines follows with the descriptions of the rows. Each line has length m and contains only digits ‘0’ and ‘1’.

Output
Output a single integer — the minimum possible number of ones you can get after applying some sequence of operations.

Example
inputCopy
3 4
0110
1010
0111
outputCopy
2
C.二进制表
每次测试的时间限制6秒
每次测试的内存限制256兆字节
输入标准输入
产量标准输出
您将获得一个由n行和m列组成的表。表的每个单元格包含0或1。在一个步骤中，您可以选择任何行或任何列并反转所有值，即将0替换为1，反之亦然。

在应用一些操作后，您可以获得值为1的最小单元格数是多少？

输入
输入的第一行包含两个整数Ñ和米（1≤  Ñ  ≤20，1≤  米  ≤100 000） -行的，分别的数量和列的数量。

然后n行跟随行的描述。每行的长度为m，仅包含数字“ 0 ”和“ 1 ”。

产量
输出一个整数 - 应用一系列操作后可以获得的最小数量。

例
输入复制
3 4
0110
1010
0111
产量复制
2

题解

就是给出一个01矩阵，每次可以把一行或一列取反
求所有可能的矩阵中最小的1个数

因为n很小，所以考虑状压n
如果行的方案确定了，那么答案就是每一列异或行后取反与否的最大值之和

---

设f(s)表示当行选取的状态为s时的答案
设ans(s)表示某一列状态为s时的答案
要考虑整列取反的情况
设g(s)表示初始列状态为s的列数
则
f(s)=∑s⊕s′=kans(k)g(s′) f ( s ) = ∑ s ⊕ s ′ = k a n s ( k ) g ( s ′ )
等于是枚举每一种可能的列，然后进行列的取反，答案就是所有列之和
可以变成
f(s)=∑s=k⊕s′ans(k)g(s′) f ( s ) = ∑ s = k ⊕ s ′ a n s ( k ) g ( s ′ )
就是FWT的形式了

code

// codeforces 662C Binary Table
// start:25/08/17
#include 
#include 
#include 
#include 
#include 
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define min(a,b) (a
using namespace std;

typedef long long AA[1048576];
int A[100001];
AA s,a,b,c;
int n,m,i,j,k,l,Len;
char ch;
long long ans;

void tf(long long *a)
{
    int i,j,k,l;
    int S=1,s1=1,s2=Len+1;

    fo(i,1,n)
    {
        S<<=1;
        s2>>=1;

        fo(j,0,s2-1)
        {
            fo(k,0,s1-1)
            {
                l=j*S+k;
                s[l]=a[l]+a[l+s1];
                s[l+s1]=a[l]-a[l+s1];
            }
        }

        memcpy(a,s,sizeof(long long)*(Len+1));

        s1<<=1;
    }
}

void utf(long long *a)
{
    int i,j,k,l;
    int S=1,s1=1,s2=Len+1;

    fo(i,1,n)
    {
        S<<=1;
        s2>>=1;

        fo(j,0,s2-1)
        {
            fo(k,0,s1-1)
            {
                l=j*S+k;
                s[l]=(a[l]+a[l+s1])>>1;
                s[l+s1]=(a[l]-a[l+s1])>>1;
            }
        }

        memcpy(a,s,sizeof(long long)*(Len+1));

        s1<<=1;
    }
}

int main()
{
    scanf("%d%d",&n,&m); Len=pow(2,n)-1;
    fo(i,1,n)
    {
        scanf("\n");
        fo(j,1,m)
        {
            scanf("%c",&ch);
            A[j]=(A[j]<<1)+(ch-'0');
        }
    }

    fo(i,1,m)
    b[A[i]]++;
    fo(i,0,Len)
    {
        j=i;
        k=0;
        while (j)
        {
            k+=j&1;
            j>>=1;
        }
        a[i]=min(k,n-k);
    }

    tf(a);
    tf(b);

    fo(i,0,Len)
    c[i]=a[i]*b[i];

    utf(c);

    ans=233333333;
    fo(i,0,Len)
    ans=min(ans,c[i]);

    printf("%I64d\n",ans);
}