线性DP做题整合
第1行:整数序列的长度N(2 <= N <= 50000) 第2 - N+1行:N个整数
输出最小正子段和。
8 4 -1 5 -2 -1 2 6 -2
1
转自光速小丸子:
对每一位来说,计算从第一位到该位置的数字的和。然后对这些和排序。
如果相近的位置上的node满足其pos的前后关系,就比较最小值,因为是相近的,所以已经是最小值候选了,其余的绝对不可能了,因为如果A到B不能形成队列,A到C形成队列了,那么B到C一定是比A到C的数值更小,而且还一定能够形成队列(A与B不能形成队列,说明posA>posB,A与C能形成队列,说明posA
这个题夹克老师太厉害了,膜拜~
另外自己还要注意一点的就是,以后一旦是连续序列这样的题目,自己第一时间需要想到的就是前缀和可能会发挥作用,碰到过好多次了还没有记性。
思路:根据权值排个序, 这样对于每个元素, 如果前后两个元素符合条件, 那么这是对于这个元素来说最优的了, 当时想 对于一个元素, 会不会有左面哪个不符合, 前面某个符合,他跟前面那个是最终答案, 手写一下pos,发现如果他跟前面那个符合, 那么他左面那个一定跟前面那个符合, 所以这永远不会是正确答案
- #include
- #include
- #include
- #include
- using namespace std;
- const int maxn = 5e4 + 7;
- typedef long long ll;
- struct node
- {
- ll val;
- int pos;
- node()
- {
- val = 0;
- pos = 0;
- }
- }a[maxn];
- int cmp(const node &a,const node &b)
- {
- if(a.val == b.val)
- return a.pos > b.pos; //贪心构造符合的数列
- return a.val < b.val;
- }
- int main()
- {
- int n;
- ll x;
- a[0].val = a[0].pos = 0;
- scanf("%d", &n);
- for(int i = 1; i <= n; i++)
- {
- scanf("%lld", &x);
- a[i].val = a[i-1].val + x;
- a[i].pos = i;
- }
- sort(a, a+1+n, cmp);
- ll ans = 1e18;
- for(int i = 1; i <= n; i++)
- {
- if(a[i].val > a[i-1].val && a[i].pos > a[i-1].pos)
- {
- ans = min(ans, a[i].val - a[i-1].val);
- }
- // cout << a[i].val << endl;
- }
- printf("%lld\n", ans);
- return 0;
- }
第1行:M和N,中间用空格隔开(2 <= M,N <= 500)。 第2 - N + 1行:矩阵中的元素,每行M个数,中间用空格隔开。(-10^9 <= M[i] <= 10^9)
输出和的最大值。如果所有数都是负数,就输出0。
3 3 -1 3 -1 2 -1 3 -3 1 2
7
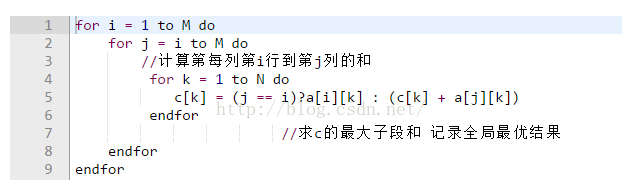
我们看看标为红色的部分 就是求每列第i行到第j行之间的所有数的和,我们没有再用一个循环求,而是随着j的增长,每次把第j行的结果叠加到之前的和上。 另外求c的最大子数组和是个线性时间算法,实际上它可以和那个k的for循环合并在一起,不过不影响时间复杂度。时间复杂度是O(M^2N)。
总的来说就是 n2枚举所有列的组合, 然后求出每一行在这两列之间的和(这里随着j的移动求就好了,o1复杂度,不比再一个for从头枚举), 答案就是 最大子段和了, 求一段连续的区间,让他们和最大, 只不过这里区间每个数代表的是一段数的和, 巧妙的将n5复杂度的算法通过枚举变成了n3了~
总结:当让求一个区间, 一个二维区间的题目的时候, 可以枚举左端点/左右限制/列,剩下的通过某种算法求解,很多题目都是讲二维变为1维,之前做过把i跟j分开的,这题也是一个套路
- #include
- #include
- #include
- #include
- using namespace std;
- const int maxn = 505;
- int a[maxn][maxn], sum[maxn];
- int main()
- {
- int m, n;
- scanf("%d%d", &m, &n);
- for(int i = 1; i <= n; i++)
- for(int j = 1; j <= m; j++)
- scanf("%d", &a[i][j]);
- int cur = 0, ans = 0;
- for(int i = 1; i <= m; i++)
- {
- for(int j = i; j <= m; j++)
- {
- cur = 0;
- for(int k = 1; k <= n; k++)
- {
- sum[k] = i == j ? a[k][j] : sum[k]+a[k][j];
- cur += sum[k];
- if(cur < 0) cur = 0;
- ans = max(ans, cur);
- }
- }
- }
- printf("%d\n", ans);
- return 0;
- }
codeforces 687C
网上一个人题解写的很好,也挺明白的:点击打开链接
题意:给定n(1 <= n <= 500)个硬币,每个硬币都有面值,求每个能构成和为k(1 <= k <= 500)的硬币组合中,任意个数相互求和的总额种类,然后将所有硬币组合中最后得到的结果输出。
一维表示总额,二维表示能否由一维的总额得出此额度。
假如枚举到的硬币面值为 t ,如果存在dp[ i - t ] [ j ] = true,那么有
1、dp[ i ] [ j ] = true; 相当于总额里增加一个 t 的面值的硬币,但实际组成 j 的额度时并没有用到它。
2、dp[ i ] [ j + t ] = true; 相当于总额里增加一个 t 的面值的硬币,并且用它构成了新达到的额度 j + t。
初始化dp[ 0 ] [ 0 ] = true; 总额为 0 时,能构成 0 额度。
为了防止二次利用此硬币,总额需从 k 递减至 t。(否则的话若从 t 递增至 k ,条件判断时会重复利用刚刚由此面值得到的新额度,即刚刚使用此硬币标为true的项,造成此硬币二次利用)
最后只需要统计总额为 k 时能达到的额度,并且输出即可。
总结:很惭愧,我自己没做出这题来,太菜了。。做的时候直接就去怼 前i个组成j 能有几个答案了, 然而发现好难转移啊, 想了一个要用好几个数组维护的做法, 感觉思路肯定错了- -,就没耐心的看题解了, 发现自己好菜啊, v8说过, 先要表示状态, 把这题的几个状态都写出来, 看看哪个放在下标里,哪些表示就好了, 我为什么要那么转移啊。。这题状态是这样的, 凑出的总和, 随意凑出的额数,当前用了几个,好像没了, 经验少就不断往上凑啊, 发现前两个很好转移,dp代表能不能凑到。。以后dp不一定一定要记录答案, 也可以记录状态 ,之前做过这样的题。。 记录状态的题一般数据量比较小, 还有dp不会状态,就先把所有状态列出来
#include
#include
#include
#include
using namespace std;
const int maxn = 5e2 + 5;
int dp[maxn][maxn], a[maxn], ans[maxn], cnt, n, k;
int main()
{
while(~scanf("%d%d", &n, &k))
{
for(int i = 1; i <= n; i++)
scanf("%d", &a[i]);
dp[0][0] = 1;
for(int i = 1; i <= n; i++)
for(int v = k; v >= a[i]; v--) //这里要倒着写,如果正着写,会被前面刚加的硬币影响。。。以后可以这样判断
for(int j = 0; j+a[i] <= k; j++)
{
if(dp[v-a[i]][j])
dp[v][j] = dp[v][j+a[i]] = 1;
}
int cnt = 0;
for(int i = 0; i <= k; i++)
if(dp[k][i])
ans[cnt++] = i;
printf("%d\n", cnt);
for(int i = 0; i < cnt; i++)
printf("%d ", ans[i]);
}
return 0;
}
HDU 4960 Another OCD Patient
题意:
给定一个n长的序列vi,现在要求合并连续子序列,使得最终的序列式一个回文序列。每次合并i长的子序列,需要花费ai。求最小花费。
思路:首先研究明白题意, 回文串, 特点是 前后对应位置相同, 这题又是合并, 所以我们可以从这入手,开头和结尾要合并成相同的值,抛去已经合并的开头和结尾,剩下的又要合并相同的值,如此反复知道这个序列都变成了回文,这题的状态是什么, 其实只需要知道当前区间就好了。即我把头尾合并完了是回文的了, 我就要用两个指针找下两个位置让他们相同,可以选这个位置,也可以不选,那就是dp啦,用记忆化搜索写起来比较方便,每次对于求的L和R,枚举i,j,使得 L-i合并之后可以与j-R合并之后回文,然后递归处理i和j即可。
总结:
dp不一定都要用递推, 想不出dp,想想记忆化怎样,复杂度其实一样, 而且dfs比较无脑,比较类似的例子是上几届山东省赛的题:点击打开链接
记忆化代码:
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int maxn = 5e3 + 5;
const ll INF = 1e18;
ll sum[maxn], v[maxn];
int cost[maxn], dp[maxn][maxn], n;
int dfs(int l, int r) //很清楚
{
if(dp[l][r] != -1) return dp[l][r];
int ans = cost[r-l+1]; //一开始一定要赋值最大使用值,而不是INF
for(int i = l, j = r; i < j;) //用两个指针。。
{
ll sum1 = sum[i]-sum[l-1];
ll sum2 = sum[r]-sum[j-1];
if(sum1 == sum2)
ans = min(ans, dfs(i+1, j-1) + cost[i-l+1] + cost[r-j+1]), i++, j--; //这还是很通俗易懂把,两个指针把所有情况都枚举到了
else if(sum1 < sum2) i++;
else j--;
}
return dp[l][r] = ans;
}
int main()
{
while(~scanf("%d", &n), n)
{
memset(dp, -1, sizeof(dp));
memset(sum, 0, sizeof(sum));
for(int i = 1; i <= n; i++)
scanf("%lld", &v[i]), sum[i] = sum[i-1] + v[i];
for(int i = 1; i <= n; i++)
scanf("%d", &cost[i]);
printf("%d\n", dfs(1, n));
}
return 0;
} | CodeForces 714E | Sonya and Problem Wihtout a Legend |
题目大意是给定n个数字和一种操作,该操作允许你将其中某个数字+1或者-1,求使n个数字变更为严格单调递增所需的最小操作数.
#include
#include
#include
#include
#include
typedef long long ll;
using namespace std;
priority_queue pq;
int main()
{
ll n, x, ans = 0;
scanf("%lld%lld", &n, &x);
pq.push(x-1); //不必严格递增就不用减
for(int i = 2; i <= n; i++)
{
scanf("%lld", &x);
x -= i;
pq.push(x);
if(pq.top() > x)
{
ans += pq.top() - x;
pq.pop();
pq.push(x);
}
}
printf("%lld\n", ans);
}
HDU - 5763 Another Meaning dp +KMP
题意:给定一个字符串和模板串,告诉你模板串有2个意思,问这个字符串总共有多少种含义。
思路:dp[i]表示以i字符串结尾的串的总含义数.那么有dp【i】=dp[i-1] 如果他可以和模式串匹配,dp[i-1]表示
他不表示模式串的那个意思.如果 主串中第i个位置往前lenb个字符构成的串和模式串匹配,
dp[i]=(dp[i-1]+dp[i-lenb]);表示匹配模式串的那个意思.
KMP时候,我们匹配到j==lenb时就把主串第i个字符标记一下,含义就是当前i字符往前lenb个字符的字符串可以和模式串匹配.这样就实现了O(N)预处理O(1)查询.
#include
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
const int maxn = 1e5+10;
char a[maxn],b[maxn];
ll dp[maxn];
bool mat[maxn];
int nxt[maxn];
void get_nxt()
{
int len = strlen(b+1);
nxt[1] = -1;
int i = 1,j = 0;
while(i <= len)
{
if(j == 0 || b[i] == b[j])
nxt[++i] = ++j;
else
j = nxt[j];
}
}
void KMP()
{
int i=1,j=1;
int lena = strlen(a+1);
int lenb = strlen(b+1);
while(i<=lena)
{
if(j==0||a[i]==b[j])
{
if(j==lenb)
{
mat[i] = 1;
j=nxt[j];
}
else
{
i++,j++;
}
}
else
j=nxt[j];
}
return ;
}
int main()
{
int _;
cin>>_;
int t = 0;
while(_--)
{
memset(dp,0,sizeof dp);
memset(mat,0,sizeof mat);
scanf("%s %s",a+1,b+1);
int lena=strlen(a+1);
int lenb=strlen(b+1);
get_nxt();
dp[0] = 1;
KMP();
for(int i = 1;i <= lena;i++)
{
dp[i] = dp[i-1];
if(mat[i])
dp[i] = (dp[i] + dp[i-lenb])%mod;
}
printf("Case #%d: %lld\n",++t,dp[lena]);
}
return 0;
} UVA 12260 Free Goodies
题意
Petra和Jan分n个糖果,每个人轮流拿,一次只能拿一个,抽签决定谁先开始拿
每个糖果有两个值x,y, 如果Petra拿了会获得值x, Jan拿了会获得值y
Petra每次都选择对自己价值最大的(x最大)拿,如果有多个x相同大,选择y值最小的
Jan选择的策略是,要让自己最终获得的总价值最大, 并且在这个的前提下,要让Petra的值也尽量大
问最终他们获得的价值各是多少?
我们可以知道Petra直接贪心选取即可。所以对糖果的p进行排序,就看Jan会取哪些糖果了,那么每个糖果就可以看成是Jan取不取,但是要注意,由于Petra是一定会取一个剩下的p最大的,所以Jan取糖果的时候是有一定的限制的,限制为:如果Jan先取,1个糖果,Jan可以拿到一个;2个糖果,Jan可以拿其中一个;3个糖果Jan可以拿其中2个;4个糖果也是2个...以此类推,Jan能拿的糖果数为(i + 1)/2。因此dp[i][j]表示Jan在前i个糖果中拿了j个,j <= (i + 1)/2.注意有先后手问题,我们只需考虑Jan先拿,如果Petra先拿就直接从第二个开始变成Jan先手。
转移方程:dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]+a[i].y)取或不取
总结:
这题提前排了个序, 这样就保证了pet直接顺着从前面拿没被拿过的就好了, 这样dp保证了两个物品,dp的决策可能包含其中一个物品,因为排了个序。
#include
#include
#include
#include
using namespace std;
const int maxn = 1e3 + 5;
int dp[maxn][maxn], cost[maxn][maxn];
struct node
{
int p, j;
}a[maxn];
int cmp(const node &a, const node &b)
{
if(a.p == b.p)
return a.j < b.j;
else
return a.p > b.p;
}
char name[100];
int main()
{
int _, n, s, sum, cnt;
cin >> _;
while(_--)
{
memset(dp, 0, sizeof(dp));
s = 1, sum = 0, cnt = 0;
scanf("%d", &n);
scanf(" %s", name);
if(name[0] == 'P') s = 2;
for(int i = 1; i <= n; i++)
scanf("%d%d", &a[i].p, &a[i].j), sum += a[i].p;
sort(a+1, a+1+n, cmp);
for(int i = s; i <= n; i++)
{
cnt++;
for(int j = 1; j <= (cnt+1)/2; j++)
{
dp[i][j] = dp[i-1][j];
cost[i][j] = cost[i-1][j];
if(dp[i-1][j-1]+a[i].j > dp[i][j])
{
dp[i][j] = dp[i-1][j-1]+a[i].j;
cost[i][j] = cost[i-1][j-1]+a[i].p;
}
else if(dp[i-1][j-1]+a[i].j == dp[i][j])
cost[i][j] = min(cost[i][j], cost[i-1][j-1]+a[i].p);
}
}
printf("%d %d\n", sum-cost[n][(cnt+1)/2], dp[n][(cnt+1)/2]);
}
return 0;
} 超大01背包,卡内存, 所以要单调性优化一下。。
#include
#include
#include
#include 第1行:整数序列的长度N(2 <= N <= 50000) 第2 - N+1行:N个整数
输出最小正子段和。
8 4 -1 5 -2 -1 2 6 -2
1
转自光速小丸子:
对每一位来说,计算从第一位到该位置的数字的和。然后对这些和排序。
如果相近的位置上的node满足其pos的前后关系,就比较最小值,因为是相近的,所以已经是最小值候选了,其余的绝对不可能了,因为如果A到B不能形成队列,A到C形成队列了,那么B到C一定是比A到C的数值更小,而且还一定能够形成队列(A与B不能形成队列,说明posA>posB,A与C能形成队列,说明posA
这个题夹克老师太厉害了,膜拜~
另外自己还要注意一点的就是,以后一旦是连续序列这样的题目,自己第一时间需要想到的就是前缀和可能会发挥作用,碰到过好多次了还没有记性。
思路:根据权值排个序, 这样对于每个元素, 如果前后两个元素符合条件, 那么这是对于这个元素来说最优的了, 当时想 对于一个元素, 会不会有左面哪个不符合, 前面某个符合,他跟前面那个是最终答案, 手写一下pos,发现如果他跟前面那个符合, 那么他左面那个一定跟前面那个符合, 所以这永远不会是正确答案
- #include
- #include
- #include
- #include
- using namespace std;
- const int maxn = 5e4 + 7;
- typedef long long ll;
- struct node
- {
- ll val;
- int pos;
- node()
- {
- val = 0;
- pos = 0;
- }
- }a[maxn];
- int cmp(const node &a,const node &b)
- {
- if(a.val == b.val)
- return a.pos > b.pos; //贪心构造符合的数列
- return a.val < b.val;
- }
- int main()
- {
- int n;
- ll x;
- a[0].val = a[0].pos = 0;
- scanf("%d", &n);
- for(int i = 1; i <= n; i++)
- {
- scanf("%lld", &x);
- a[i].val = a[i-1].val + x;
- a[i].pos = i;
- }
- sort(a, a+1+n, cmp);
- ll ans = 1e18;
- for(int i = 1; i <= n; i++)
- {
- if(a[i].val > a[i-1].val && a[i].pos > a[i-1].pos)
- {
- ans = min(ans, a[i].val - a[i-1].val);
- }
- // cout << a[i].val << endl;
- }
- printf("%lld\n", ans);
- return 0;
- }
第1行:M和N,中间用空格隔开(2 <= M,N <= 500)。 第2 - N + 1行:矩阵中的元素,每行M个数,中间用空格隔开。(-10^9 <= M[i] <= 10^9)
输出和的最大值。如果所有数都是负数,就输出0。
3 3 -1 3 -1 2 -1 3 -3 1 2
7
我们看看标为红色的部分 就是求每列第i行到第j行之间的所有数的和,我们没有再用一个循环求,而是随着j的增长,每次把第j行的结果叠加到之前的和上。 另外求c的最大子数组和是个线性时间算法,实际上它可以和那个k的for循环合并在一起,不过不影响时间复杂度。时间复杂度是O(M^2N)。
总的来说就是 n2枚举所有列的组合, 然后求出每一行在这两列之间的和(这里随着j的移动求就好了,o1复杂度,不比再一个for从头枚举), 答案就是 最大子段和了, 求一段连续的区间,让他们和最大, 只不过这里区间每个数代表的是一段数的和, 巧妙的将n5复杂度的算法通过枚举变成了n3了~
总结:当让求一个区间, 一个二维区间的题目的时候, 可以枚举左端点/左右限制/列,剩下的通过某种算法求解,很多题目都是讲二维变为1维,之前做过把i跟j分开的,这题也是一个套路
- #include
- #include
- #include
- #include
- using namespace std;
- const int maxn = 505;
- int a[maxn][maxn], sum[maxn];
- int main()
- {
- int m, n;
- scanf("%d%d", &m, &n);
- for(int i = 1; i <= n; i++)
- for(int j = 1; j <= m; j++)
- scanf("%d", &a[i][j]);
- int cur = 0, ans = 0;
- for(int i = 1; i <= m; i++)
- {
- for(int j = i; j <= m; j++)
- {
- cur = 0;
- for(int k = 1; k <= n; k++)
- {
- sum[k] = i == j ? a[k][j] : sum[k]+a[k][j];
- cur += sum[k];
- if(cur < 0) cur = 0;
- ans = max(ans, cur);
- }
- }
- }
- printf("%d\n", ans);
- return 0;
- }