拓扑排序

1.概念

对于AOV网，我们只需要知道一个AOV网一定是一个有向无环图(Directed Acyclic Graph,DAG)。

拓扑排序，是一个只适合AOV网的算法。

2.拓扑排序

拓扑排序的目标是将所有节点排序，使得排在前面的节点不能依赖于排在后面的节点。因此只有有向无环图可以进行拓扑排序，因为环中的每一个点都有依赖，无法排序。

具体流程

1.首先选择一个入度为0的点
2.删除此顶点以及与此顶点相关联的边
3.重复，知道选不出点了
4.如果ans的个数不等于n，则说明图有环

代码

#include 
using namespace std;
int n,m,r[205],ans[205],cnt;
bool a[205][205];

int main() {
	scanf("%d %d",&n,&m);
	for(int i=1,u,v;i<=m;i++) {
		scanf("%d %d",&u,&v);
		a[u][v]=1,r[v]++;
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=n;j++) {
			if(r[j]==0) {
				ans[++cnt]=j，r[j]--;
				break;
			}
		}
		for(int j=1;j<=n;j++)
			if(a[ans[cnt]][j]) r[j]--;
	}
	if(cnt!=n)
		printf("no solution");
	else {
		for(int i=1;i<=cnt;i++)
			printf("%d ",ans[i]);
	}
	return 0;
}

我们改为邻接表存储和队列存点。

#include 
#include 
#include 
using namespace std;
int n,m,r[205];
vector a[205],ans;

struct node {
	int z;
	bool operator <(const node y) const { return z>y.z; }
	node(int Z) { z=Z; }
};
priority_queue q;

int main() {
	scanf("%d %d",&n,&m);
	for(int i=1,u,v;i<=m;i++) {
		scanf("%d %d",&u,&v);
		a[u].push_back(v),r[v]++;
	}
	for(int i=1;i<=n;i++)
		if(r[i]==0) q.push(node(i));
	while(q.size()) {
		node p=q.top();
		q.pop();
		ans.push_back(p.z);
		for(int i=0;i

写一个小根堆太麻烦了，有一个简单的方法。

#include 
#include 
#include 
using namespace std;
int n,m,r[205];
vector a[205],ans;
priority_queue q;

int main() {
	scanf("%d %d",&n,&m);
	for(int i=1,u,v;i<=m;i++) {
		scanf("%d %d",&u,&v);
		a[u].push_back(v),r[v]++;
	}
	for(int i=1;i<=n;i++)
		if(r[i]==0) q.push((i*-1));
	while(q.size()) {
		int p=q.top();
		p*=-1;
		q.pop();
		ans.push_back(p);
		for(int i=0;i

其实，拓扑排序就是搜索。
大家完全就可以用搜索打拓扑排序。

3.例题

平板涂色

传送门
题目描述
$CE$ 数码公司开发了一种名为自动涂色机（$APM$）的产品。它能用预定的颜色给一块由不同尺寸且互不覆盖的矩形构成的平板涂色。

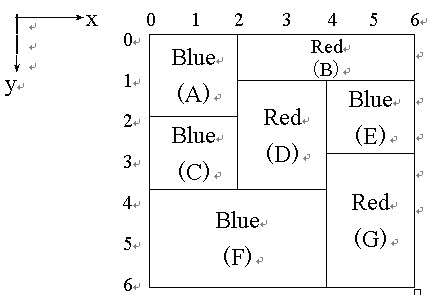
为了涂色，APM 需要使用一组刷子。每个刷子蘸了颜色$C$。$APM$ 拿起一把蘸有颜色$C$的刷子，并给所有颜色为$C$的矩形涂色。请注意，涂色有顺序要求：为了避免颜料渗漏使颜色混合，一个矩形只能在所有紧靠它上方的矩形涂色后，才能涂色。例如图中矩形$F$必须在$C$和$D$涂色后才能涂色。注意，每一个矩形必须立刻涂满，不能只涂一部分。

写一个程序求一个使 APM 拿起刷子次数最少的涂色方案。注意，如果一把刷子被拿起超过一次，则每一次都必须记入总数中。

输入格式
第一行为矩形的个数$N$。
下面有$N$行描述了$N$个矩形。每个矩形有$5$个整数描述，左上角的$y$坐标和$x$坐标，右下角的$y$坐标和$x$坐标，以及预定颜色。

输出格式
一行一个整数，表示拿起刷子的最少次数。

样例

样例输入：								样例输出：
7										3
0 0 2 2 1
0 2 1 6 2
2 0 4 2 1
1 2 4 4 2
1 4 3 6 1
4 0 6 4 1
3 4 6 6 2

数据范围与提示
对于全部数据，$1\le N\le 14$，颜色号为$1$到$20$的整数。保证平板的左上角坐标总是$(0,0)$，坐标的范围是$0$到$9$。

思路

数据范围水到炸裂，怎么看都是DFS好吧？
当然，虽然数据范围水到炸，我还是写了两个剪枝：
1.最优化剪枝：当前涂色次数大于等于当前答案，直接回溯
2.可行性剪枝：如果当前一个砖都没有涂到，直接回溯

代码

#include 
using namespace std;
struct node{
    int a1,b1,a2,b2,x;
}a[20];
bool l=0;
int n,m,ans=0x3f3f3f3f,b[20],f[20][20],y[20];

int cmp(node a,node b) { return a.a1!=b.a1?(a.a1=ans) return;
    if(pq==n) {
        ans=t;
        return ;
    }
    for(int i=1;i<=m;i++) {
        int cnt=0;
        if(i!=xx && y[i]) {
            for(int j=1;j<=n;j++) {
            	if(!b[j] && a[j].x==i && yu(j))
                    b[j]=1,cnt++;
                else if(b[j] && a[j].x==i)
                	b[j]++;
			}   
            if(cnt>0) dfs(t+1,pq+cnt,i);
            for(int j=n;j>=1;j--) {
            	if(b[j]==1 && a[j].x==i && yu(j))
                    b[j]=0,cnt--;
                else if(b[j]>1 && a[j].x==i)
                	b[j]--; 
			}
        }
    }
    return ;
}

int main() {
	scanf("%d",&n);
    for(int i=1;i<=n;i++) {
    	scanf("%d %d %d %d %d",&a[i].a1,&a[i].b1,&a[i].a2,&a[i].b2,&a[i].x);
    	a[i].a1++,a[i].b1++,y[a[i].x]++;
	}
    for(int i=1;i<=20;i++)
    	if(y[i]) m=i;
    sort(a+1,a+n+1,cmp);
    for(int i=2;i<=n;i++) {
    	for(int j=i-1;j>=1;j--) {
    		if(a[i].a1==a[j].a2+1 && ((a[i].b1>=a[j].b1 && a[i].b1<=a[j].b2) || (a[i].b2>=a[j].b1 && a[i].b2<=a[j].b2)))
                f[i][j]=1;
		}
	}
    dfs(0,0,0);
    printf("%d",ans);
    return 0;
}

菜肴制作

传送门
题目描述
知名美食家小$A$被邀请至$ATM$大酒店，为其品评菜肴。

$ATM$酒店为小$A$准备了$N$道菜肴，酒店按照为菜肴预估的质量从高到低给予$1$到$N$的顺序编号，预估质量最高的菜肴编号为$1$。由于菜肴之间口味搭配的问题，某些菜肴必须在另一些菜肴之前制作，具体的，一共有$M$条形如「 $i$号菜肴『必须』先于$j$号菜肴制作”的限制」，我们将这样的限制简写为$(i,j)$。

现在，酒店希望能求出一个最优的菜肴的制作顺序，使得小 A 能尽量先吃到质量高的菜肴：也就是说，

在满足所有限制的前提下，$1$号菜肴「尽量」优先制作；
在满足所有限制，$1$号菜肴「尽量」优先制作的前提下，$2$号菜肴「尽量」优先制作；
在满足所有限制，$1$号和$2$号菜肴「尽量」优先的前提下，$3$号菜肴「尽量」优先制作；
在满足所有限制，$1$号和$2$号和$3$号菜肴「尽量」优先的前提下，$4$号菜肴「尽量」优先制作；
以此类推。
无解输出“Impossible!” （不含引号，首字母大写，其余字母小写）

输入格式
第一行是一个正整数$D$，表示数据组数。
接下来是$D$组数据。
对于每组数据：
第一行两个用空格分开的正整数$N$和$M$，分别表示菜肴数目和制作顺序限制的条目数。
接下来$M$行，每行两个正整数$x,y$ ，表示「$x$号菜肴必须先于$y$号菜肴制作」的限制。（注意：$M$条限制中可能存在完全相同的限制）

输出格式
输出文件仅包含$D$行，每行$N$个整数，表示最优的菜肴制作顺序，或者”Impossible!”表示无解（不含引号）。

样例

样例输入：								样例输出：
3 										1 5 3 4 2 
5 4 									Impossible! 
5 4 									1 5 2 4 3
5 3 
4 2 
3 2 
3 3 
1 2 
2 3 
3 1 
5 2 
5 2 
4 3

数据范围与提示
对于$100\%$的数据，$N,M\le 100000,D\le 3$。

思路

看到题目，可以想到拓扑排序。但是如果要求字典序最小的排列，那就错了。
可以举出反例：4种菜肴，限制为(2,4)(3,1)，

那么字典序最小的是2,3,1,4，但题目要求的最优解是3,1,2,4。

继续考虑，可以发现，如果最后一个数字在合法范围内尽可能大，那么这样是绝对有利的。

因为如果设最后一个数字是x，那么除了x之外的所有数都不会被放到最后一个位置。

而这样就可以让前面所有小于x的数都尽量靠前（大于x的数，虽然也能靠前，但由于x的位置已经固定，因此没有用），达到题目的目标。

因此，最优解就是符合条件的排列中，反序列的字典序最大的排列。

所以，在反图上跑拓扑排序，求最大字典序。在实现上，由于需要多次找出队列中的最大值，因此用堆代替队列。

代码

#include 
#include 
#include 
using namespace std;
int n,m,r[100005];
vector a[100005],ans;
priority_queue q;

int main() {
	int T;
	scanf("%d",&T);
	while(T--) {
		memset(r,0,sizeof(r));
		scanf("%d %d",&n,&m);
		for(int i=1;i<=n;i++)
			a[i].clear();
		ans.clear();
		for(int i=1,u,v;i<=m;i++) {
			scanf("%d %d",&u,&v);
			a[v].push_back(u),r[u]++;
		}
		for(int i=1;i<=n;i++)
			if(r[i]==0) q.push(i);
		while(q.size()) {
			int p=q.top();
			q.pop();
			ans.push_back(p);
			for(int i=0;i=0;i--)
				printf("%d ",ans[i]);
		}
		else
			printf("Impossible!");
		printf("\n");
	}
	return 0;
}