单词查找树Trie
Table of Contents
R向单词查找树
查找
插入
前缀匹配
通配符匹配
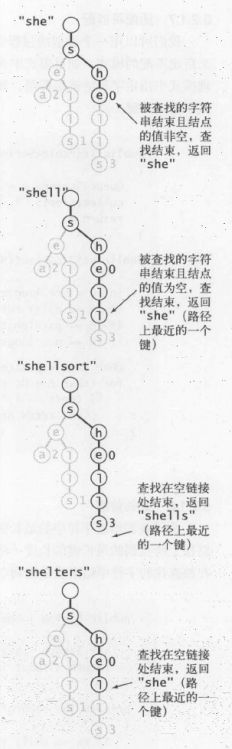
最长前缀
删除操作
R向单词查找树性能
三向单词查找树
关于查找算法一般使用符号表,例如二叉查找树,红黑树以及散列表等。当键值为字符串时可以使用单词查找树来构建单词树,实现字符串的快速查找以及其他操作,基本特性是:
查找命中所需时间与待查找键的长度成正比;
查找未命中只需检查若干个字符。
R向单词查找树
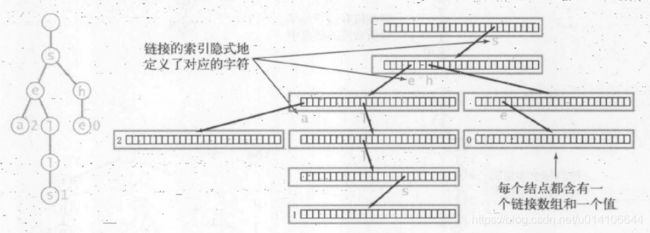
假定存储的字符串字母表基数为R,即组成字符串的字符集合最大为R中,对应于字母表,可以用索引[0,R-1]来表示各个字符,可以参考与ASCII。对于单词查找树的每一个节点由一个Value值以及R维数组组成,其中R维数组保存了下一个字符的可能性,根节点其Value值为null。例如组成字符串的字母集合为小写字母,即R=26。此时如果数组next[0]非空,则说明下一个字符取值可能为a,next[25]非空则说明下一个字符取值可能为z。
private static int R = 256;//字母表的基数
private Node root;
//java不支持范型数组 val为Object类型
private static class Node{
Object val;
//每一个节点都持有一个Node[R]用来保存下一个字符所有可能情况基数R
Node[] next = new Node[R];
}因此如果得到了当前字符Node节点,可以利用next数组取值来快速确定下一个字符取值的可能性以及位置。
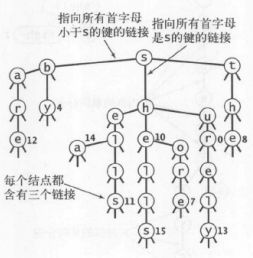
单词查找树的重要性质:
每个节点都含有R个连接,对应每个可能出现的字符;
字符和键隐式保存在数据结构中;
键是从根节点到含有非空值的节点路径隐式表示的。例如以上键sea,sells,she。
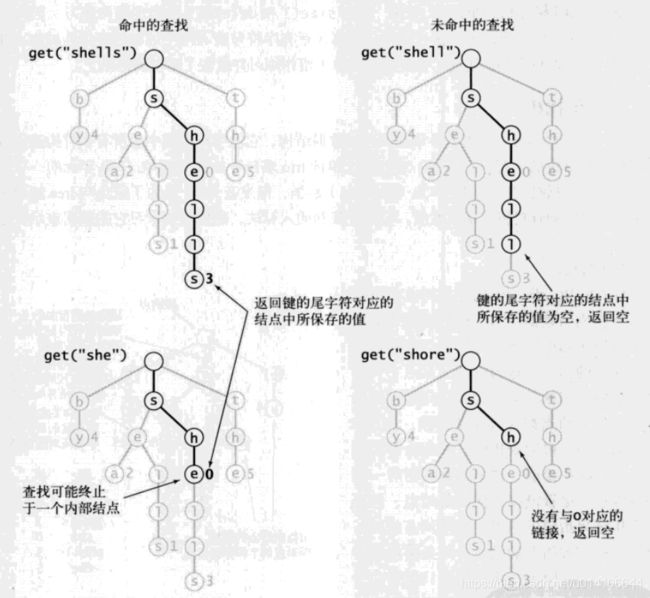
查找
从根节点开始查找:
当查找到某一节点时,此时有以下情况:
如果此时节点为空,则说明待查找键不存在,返回null;
如果此时查找路径深度等于待查找键的长度,判断此时该节点是否为空值,如果为空值,则说明不存在该键,如果不为空,则说明存在;
如果查找路径深度小于键长度,则说明可以继续往下一个字符匹配,递归匹配。
public Value get(String key){
Node x = get(root, key, 0);
if(x == null) return null;
return (Value) x.val;
}
private Node get(Node x, String key, int d) {
//查找结束于一条空链 该key不存在
if(x==null) return null;
//查找结束于某一个节点,判断该节点val值是否为空
if(d==key.length()) return x;
//查找未结束,继续查找第d+1个字符
char c = key.charAt(d);
return get(x.next[c], key, d+1);
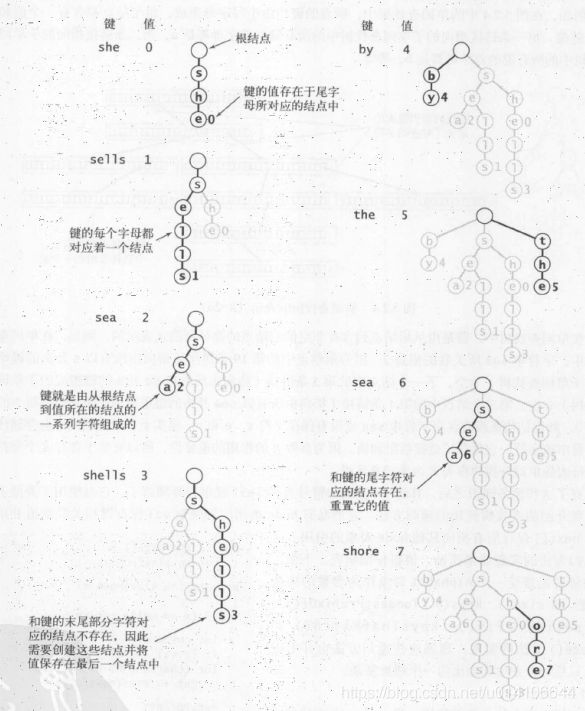
}插入
插入时注意单词查找树的性质:
键的每一个字母都对应一个节点;
键的值存储于尾字母对应的节点中;
键由根节点到其值所在节点路径上一系列字符组成的;
因此插入新键时,类似于查找算法,沿着键所在路径进行查找,如果键的某个字符不存在相应节点则新建,同时要记录查找的深度,判断是否已经到达键的尾字符位置,如果到达,则将值赋值给尾字符;否则继续查找下一个字符。
public void put(String key, Value val){
root = put(root, key, val, 0);
}
private Node put(Node x, String key, Value val, int d) {
//如果当前节点为空,则说明该节点字符不存在则新建节点
if(x==null)
x = new Node();
//判断查找路径深度是否等于键长度,如果相等则说明该节点即为目标节点,将值赋值
if(d==key.length()){
x.val = val;
return x;
}
//继续往下寻找合适的插入位置
char c = key.charAt(d);
x.next[c] = put(x.next[c], key, val, d+1);
return x;
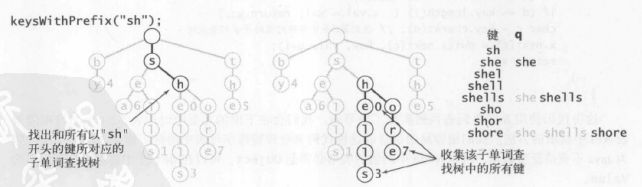
}前缀匹配
获取以给定字符串为前缀的所有键,首先找到给定字符串的尾字符位置,然后从尾字符开始遍历尾字符下一个字符的所有可能情况,即判断尾字符节点next数组哪些非空即可。
public Iterable keys(){
return keysWithPrefix("");
}
private Iterable keysWithPrefix(String pre) {
Queue q = new LinkedList<>();
collect(get(root, pre, 0), pre, q);
return q;
}
private void collect(Node x, String pre, Queue q) {
if(x==null)
return;
if(x.val!=null)
q.add(pre);
//以pre作为基准 添加一个字符 遍历所有可能情况
for(int c=0; c 通配符匹配
pat为模式串 pre为临时存储字符串 pre初始为空串,然后根据pat模式的每一个字符沿着单词查找树来寻找,如果pat字符为特定字符,则进入到next数组指定位置匹配,如果pat字符为通配符,则探索next数组的每一个位置进行匹配查找。
//通配符匹配 .匹配所有字符
public Iterable keysThatMatch(String pat){
Queue q = new LinkedList<>();
collect(root, "", pat, q);
return q;
}
private void collect(Node x, String pre, String pat, Queue q) {
//pre当前已经组装字符串长度
//System.out.println(pre);
int d = pre.length();
if(x==null) return;
//当前字符串长度与模式串相同,并且该节点val非空,将该字符串加入到队列中
if(d==pat.length()&&x.val!=null) q.add(pre);
if(d==pat.length()) return;
//匹配下一个字符
char next = pat.charAt(d);
//从该节点开始探索所有情况,如果当前是指定字符,则进入到字典树指定分支;
//如果当前是特殊字符,则依次匹配所有字符,尝试进入所有分支
for(int c=0; c 最长前缀
沿着单词树对于字符串进行查找匹配,利用length来记录匹配时,匹配字符的长度,当最终字符串全部完全查找匹配或者查找与空连接时,结束匹配,返回0,length即可。
//给定字符串的最长键前缀
public String longstPrefixOf(String s){
int length = search(root, s, 0, 0);
return s.substring(0, length);
}
private int search(Node x, String s, int d, int length) {
if(x == null) return length;
if(x.val != null) length = d;
if(d == s.length()) return length;
char c = s.charAt(d);
return search(x.next[c], s, d+1, length);
}删除操作
首先利用待删除key沿着单词树进行查找匹配,找到该键尾字符所在的节点,将尾字符节点Value置为null;
如果该该节点后序还有字符,则不需要处理;
如果该节点为尾节点,则需要向上继续判断该节点为父节点是否应该删除。
public void delete(String key){
root = delete(root, key, 0);
}
private Node delete(Node x, String key, int d) {
if(x==null) return null;
//找到待删除节点 将该节点置为null
if(d==key.length()){
x.val = null;
}else{
//如果没查找,则继续递归删除寻找下一个位置
char c = key.charAt(d);
x.next[c] = delete(x.next[c], key, d+1);
}
//如果x.val!=null或者x.next非空,则返回x
if(x.val!=null) return x;
for(char c=0; c对于单词树的操作,可以从根节点,键尾字符对应的节点,键长度,当前已经沿着单词树匹配的深度等理解;
R向单词查找树性能
树的最终结构与键插入顺序无关;
查找或者插入键时,访问次数最多为键长度加一;
未命中查找的平均检查节点数量为logRN;
连接数目为RN--wRN 其中w为键平均长度;
由于R向单词查找树,每一个节点都有R个连接,如果用来存储大字母表的长键,则会出现R值很大,并且树的深度过深,并且大部分空间是浪费的,因此可以对于R向单词查找树进行改进。
三向单词查找树
三向单词查找树保证树的每个节点含有三个指针,一个字符,一个值,其指针mid表示等于该字符,left小于该字符,right表示大于该字符;
private class Node{
char c;
Node left, mid, right;
Value val;
}其基本算法实现如下:
查找
由于三向单词查找树节点三指针的定义,只有当沿着mid方向进行匹配时,匹配深度才会增加
public Value get(String key){
Node x = get(root, key, 0);
if(x==null) return null;
return x.val;
}
private Node get(Node x, String key, int d) {
if(x==null) return null;
char c = key.charAt(d);
//与当前节点值不匹配,则进入到左分支与右分支,此时当前字符没有匹配,即下一步继续匹配该字符
//左分支
if(cx.c)
return get(x.right, key, d);
//当前节点还没有完全匹配key d记录已经匹配完成的字符长度
else if(d 插入
private Node put(Node x, String key, Value val, int d) {
char c = key.charAt(d);
if(x==null){
x = new Node();
x.c = c;
}
if(cx.c){
x.right = put(x.right, key, val, d);
}else if(d 前缀匹配
public Iterable keys(){
Queue queue = new LinkedList();
collect(root, "", queue);
return queue;
}
private Iterable keysWithPrefix(String pre) {
Queue q = new LinkedList<>();
Node n = get(root, pre, 0);
//System.out.println(n);
if(n == null) return null;
if(n.val != null) q.add(pre);
//System.out.println(q);
collect(n.mid, pre, q);
return q;
}
private void collect(Node x, String pre, Queue q) {
//System.out.println(pre);
if(x == null) return;
//在左分支内部匹配
collect(x.left, pre, q);
//判断当前节点
if(x.val != null) q.add(pre+x.c);
//回溯探索mid分支
pre = pre + x.c;
collect(x.mid, pre, q);
pre = pre.substring(0, pre.length()-1);
//在右分支中寻找
collect(x.right, pre, q);
} 通配符匹配
//通配符匹配 .匹配所有字符
public Iterable keysThatMatch(String pat){
Queue q = new LinkedList<>();
collect(root, "", 0, pat, q);
return q;
}
private void collect(Node x, String pre, int i, String pattern, Queue queue) {
if (x == null) return;
char c = pattern.charAt(i);
if (c == '.' || c < x.c) collect(x.left, pre, i, pattern, queue);
if (c == '.' || c == x.c) {
if (i == pattern.length() - 1 && x.val != null) queue.add(pre + x.c);
if (i < pattern.length() - 1) {
//类似于回溯算法,沿着mid向下匹配时,此时pre需要更新为pre+x.c
pre = pre + x.c;
collect(x.mid, pre, i+1, pattern, queue);
//当中间部分递归完成,需要回溯,进行右分支的匹配pre去掉x.c
pre = pre.substring(0, pre.length()-1);
}
}
if (c == '.' || c > x.c) collect(x.right, pre, i, pattern, queue);
} 最长前缀键
//给定字符串的最长键前缀
public String longestPrefixOf(String query) {
if (query.length() == 0) return null;
int length = 0;
Node x = root;
int i = 0;
//沿着三向字典树进行匹配以及记录匹配字符长度
while (x != null && i < query.length()) {
char c = query.charAt(i);
if (c < x.c) x = x.left;
else if (c > x.c) x = x.right;
//当c==x.c时,此时出现匹配,则判断该节点是否有值,继续沿mid方向匹配
else {
i++;
if (x.val != null) length = i;
x = x.mid;
}
}
return query.substring(0, length);
}单词查找树的核心要素:
根节点,键尾字符对应的节点,键长度,已经匹配的路径长度。
各种字符串查找算法比较
参考链接:
https://algs4.cs.princeton.edu/52trie/TST.java.html
https://algs4.cs.princeton.edu/52trie/TrieST.java.html
算法第四版