( 数据结构专题 )【 并查集&带权并查集 】
( 数据结构专题 )【 并查集 】
一般的并查集
主要记录节点之间的链接关系,而没有其他的具体的信息,仅仅代表某个节点与其父节点之间存在联系,它多用来判断图的连通性,如下图所示,这是一个并查集,其中箭头表示父子关系,可以看到这些边没有记录其他的任何信息。
![]()
而有的时候在这些边中添加一些额外的信息可以更好的处理需要解决的问题,在每条边中记录额外的信息的并查集就是带权并查集。
不过在此之前先来看看并查集的路径压缩:
在上边这个并查集中,如果对节点C做Find操作,最终会得到A,但是查找的过程中会先经过B,再通过Find(B)得到A,这是一个值得优化的地方,如果直接让C链接到A不是更好吗,这样就可以省去中间的操作,如果C跟A直接相隔很多节点,这个优化就极大地提升了查找的效率,也就是希望得到这样的结果:
![]()
对于普通的并查集我们一般分为三个部分——初始化,查找,合并。
初始化:把每个点所在集合初始化为其自身(即每个元素单独构成一个集合,其父结点是其本身)。
查找:查找元素所在的集合,即根节点。
合并:将两个元素所在的集合合并为一个集合(注:当我们想对两个元素进行合并时,那么必然时它们之间存在某种关系。在进行合并前,我们首先需要进行一次判断,判断这两个元素是否已经在同一个集合了,若是已经在同一个集合则没必要重复合并,若不是在同一个集合则需要合并,通常我们判断两个元素是否在同一个集合是通过查找操作查找这两个元素的父节点,若两个元素的父节点一致则是在同一集合,反之不然)
直接贴上各部分的代码吧。
int root( int x ) // 查找
{
if ( x!=pre[x] ) {
pre[x] = root(pre[x]); // 路径压缩
}
return pre[x];
}
void join( int x, int y ) //合并
{
int xx = root(x);
int yy = root(y);
if ( xx!=yy ) {
pre[xx] = yy;
}
}
int main()
{
for ( int i=1; i<=n; i++ ) { // 初始化
pre[i] = i;
}
return 0;
}
带权并查集
其实带权并查集也只有这三个部分,不过带权并查集与普通并查集不同的是带权并查集比普通并查集多了一个需要考虑的东西——权值。这个权值其实也可以说是一种关系,比如x比y高10分,这就是一种关系,凡是有性质上相同的关系的点我们都应该把他们归为一个集合。好了,现在来一个问题,假如x比y高10分,y比z高5分的话,x与z之间的关系是什么,x比z高多少分?很显而易见,x比z高15分,这是小学生都会的题目,虽然简单,不过我们可以借这个题来帮助我们理解带权并查集点和点之间的关系。我们将他们之间的关系转化为图,如下:
![]()
我们不难发现他们之间的关系其实可以转化成x->z=x->y+y->z,有些人可能不理解,为什么会得到这样一个公式,这样的公式能推广到有很多点的情况吗?这些问题相信看完下面这张图你会得到一个结论的。
![]()
啊哈!发现新大陆了吧,没错,其实呢,带权并查集点和点之间的关系就类似于我们数学上所学的向量,不管起点到终点的路径是怎么样的,只要我们的起点和终点是一样的,那么位移就必定相等。
在明白这一点之后,我们再来思考一下,如果x比z高5分,y比z高10分的话,x和y又是什么关系勒?这个我就不画了,你们自己好好动手画一下看能得出什么样的结果吧。
例题1: E - 食物链 POJ - 1182(带权并查集)
动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形。A吃B, B吃C,C吃A。
现有N个动物,以1-N编号。每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述:
第一种说法是"1 X Y",表示X和Y是同类。
第二种说法是"2 X Y",表示X吃Y。
此人对N个动物,用上述两种说法,一句接一句地说出K句话,这K句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。
你的任务是根据给定的N(1 <= N <= 50,000)和K句话(0 <= K <= 100,000),输出假话的总数。
Input
第一行是两个整数N和K,以一个空格分隔。
以下K行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中D表示说法的种类。
若D=1,则表示X和Y是同类。
若D=2,则表示X吃Y。
Output
只有一个整数,表示假话的数目。
Sample Input
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
Sample Output
3
推荐阅读:https://blog.csdn.net/niushuai666/article/details/6981689
思路:
x->y 偏移量0时( pre[x]=0 ) x和y同类
x->y 偏移量1时( pre[x]=1 ) x吃y
x->y 偏移量2时( pre[x]=2 ) x被y吃
有了这个假设,我们就可以在并查集中完成任意两个元素之间的关系转换了。
注意在路径压缩时需要更新偏移量, 在两点合并时需要更新偏移量。
补充两张图:
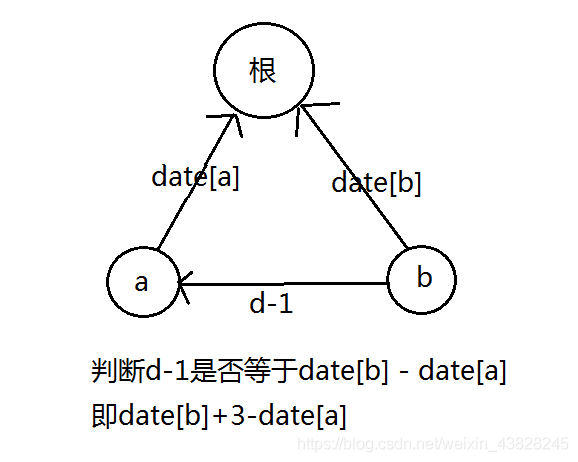
图一:当a,b同根的时候,判断a,b的关系是否正确。
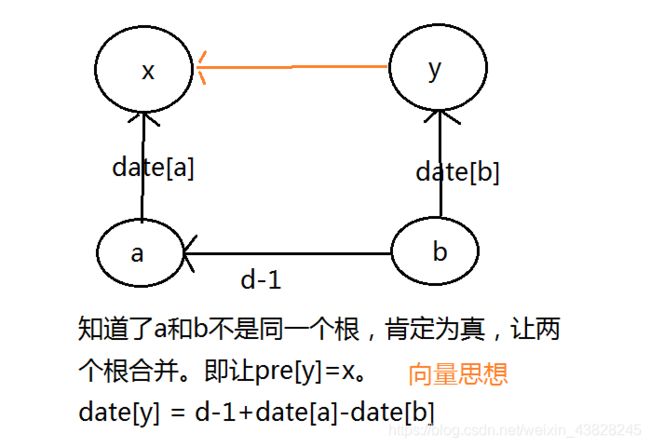
图二:当不同根时,要合并两块集合,注意权值的维护
代码:
#include
#include
using namespace std;
const int maxn = 5e4+10;
int pre[maxn];
int date[maxn];
int n,m,cnt;
int d,x,y;
int root( int x )
{
if ( x!=pre[x] ) {
int t = pre[x];
pre[x] = root(pre[x]);
date[x] = (date[x]+date[t])%3; // 在压缩路径时,更新路径权值
}
return pre[x];
}
void join( int x, int y, int d )
{
int xx = root(x);
int yy = root(y);
if ( xx==yy ) {
int now = (date[x]-date[y]+3)%3; // 关系1 ,这个地方必须+3再%3, 因为加法可能出现负值
if ( now!=d ) cnt++;
}
else {
int now = (date[y]+d-date[x]+3)%3; // 关系2
pre[xx] = yy;
date[xx] = now;
}
}
int main()
{
cin >> n >> m;
for ( int i=1; i<=n; i++ ) {
pre[i] = i;
}
cnt = 0;
while ( m-- ) {
scanf("%d %d %d",&d,&x,&y);
if ( x>n||y>n||(x==y&&d==2) ) {
cnt ++;
continue ;
}
join(x,y,d-1);
}
cout << cnt << endl;
return 0;
}
例题2: J - A Bug's Life POJ - 2492(带权并查集)
题意:有n只蜜蜂,异性配对,给出n只蜜蜂的m次配对情况,判断有没有同性恋的。
错误思路:一开始以为直接找回路就好了,结果wa了,原因是,1 3 配对 2 1 配对 那么在并查集中pre[1]=3,pre[2]=1,那么根据压缩路径pre[2] = 3,但实际上2 3 是同性的。
正确思路:带权并查集。0表示同性,1表示异性。详先代码。
#include
#include
using namespace std;
int pre[20005];
int date[20005]; // 0同行 1异性
int n,m,isp,a,b;
int root(int x) // 压缩路径,维护权值
{
if ( x!=pre[x] ) {
int t = pre[x];
pre[x] = root(pre[x]);
date[x] = ( date[x]+date[t] )%2; // 可以画图辅助推出公式
}
return pre[x];
}
void join(int a, int b)
{
int x = root(a);
int y = root(b);
if ( x==y ) {
if ( (date[a]+date[b])%2==0 ) { // a和b同性
isp = 0;
}
}
else {
pre[x] = y;
date[x] = (date[b]+date[a]+1)%2; // 画图辅助理解
}
}
int main()
{
int listt,i,j;
scanf("%d",&listt);
for ( int ji=1; ji<=listt; ji++ ) {
isp = 1;
scanf("%d %d",&n,&m);
for ( i=1; i<=n; i++ ) {
pre[i] = i;
date[i] = 0;
}
for ( i=0; i