四种方法求两个数的最大公约数

一：题目分析（求出两个数的最大公约数）

辗转相除法：
其算法过程为： 前提：设两数为a , b设其中a 做被除数,b做除数，temp为余数
1、大数放a中、小数放b中；
2、求a/b的余数；
3、若temp=0则b为最大公约数；
4、如果temp!=0则把b的值给a、temp的值给a；
5、返回第二步；

穷举法：
对两个正整数a , b如果能在区间[0，a]或[0，b]内能找到一个整数temp能同时被a和b所整除，则temp即为最大公约数。

更相减损法：

1. 任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步
2. 以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。
   则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。

Stein:
对两个正整数 x>y ：
1.均为偶数 gcd( x,y ) =2gcd( x/2,y/2 )；
2.均为奇数 gcd( x,y ) = gcd( (x+y)/2,(x-y)/2 )；
2.x奇y偶 gcd( x,y ) = gcd( x,y/2 )；
3.x偶y奇 gcd( x,y ) = gcd( x/2,y ) 或 gcd( x,y )=gcd( y,x/2 )；

二：流程图

辗转相除法

穷举法：

更相减损法

Stein

三：算法的实现

#include
#include
#include
int zzxc(int a,int b)        //辗转相除法
{
		if(a%b==0)           //如果a能被b整除，b就是最大公约数
       return b;   
else  
       return zzxc(b,a%b);        
   }
  

int gxjs(int m,int n)
{
	int i=0,temp,x;
	while(m%2==0 && n%2==0)  //判断m和n能被多少个2整除
	{
		m/=2;
		n/=2;
		i+=1;
	}
	if(mx)?n:x;     //m等于n，x中大值
		n=(n> 1;
                                x -= y;
                        }
                        else             //x是偶数，y是奇数
                        {             
                                y >>= 1;
                        }
                }
                else                  //
                {                 
                        if ( y & 0x1 )
                        {               //x是奇数，y是偶数
                                x >>= 1;
                                if ( x < y )
                                {
                                        temp = x;
                                        x = y;
                                        y = temp;
                                }
                        }
                        else                 //x,y都是奇数
                        {
                                x >>= 1;
                                y >>= 1;
                                ++factor;
                        }
                }
        }
        return ( x << factor );
}

int divisor (int a,int b) /*自定义函数求两数的最大公约数*/
{
    int  temp;          /*定义义整型变量*/
    temp=(a>b)?b:a;    /*采种条件运算表达式求出两个数中的最小值*/
    while(temp>0)     
    {
       if (a%temp==0&&b%temp==0) /*只要找到一个数能同时被a,b所整除，则中止循环*/
          break;    
       temp--;      /*如不满足if条件则变量自减，直到能被a,b所整除*/
    }
  return (temp); /*返回满足条件的数到主调函数处*/
}

#include "stdio.h"
void main()
{
	clock_t begin1, end1,begin2, end2,begin4, end4,begin3, end3;
    double cost1,cost2,cost3,cost4;
	int c[20],d[20],t1,i,m,n;

   for(i=0;i<10;i++)
   {
	 printf("请输入第%d组的两个整数\n",i+1);
	 scanf("%d %d",&c[i],&d[i]);
   }

   printf("辗转相除的结果：\n");
   begin1=clock();
   for(i=0;i<10;i++)
{
	 m=c[i];n=d[i];
	 t1=zzxc(m,n);
	 printf("第%d组的最大公约数是 %d,最小公倍数是 %d",i+1,t1,m*n/t1);/*最大公约数,最小公倍数*/
	 printf("\n");
}
    end1=clock();
    cost1 = (double)(end1 - begin1)/CLOCKS_PER_SEC;
  
	
printf("更相减损法的结果：\n");  
begin2=clock();
 for(i=0;i<10;i++)
 {	
	m=c[i];n=d[i];
   	t1=gxjs(m,n); 
	printf("第%d组的最大公约数是 %d",i+1,t1);    /*最大公约数*/
	printf("\n");
}
	end2=clock();
	cost2 = (double)(end2 - begin2)/CLOCKS_PER_SEC;
    
	
printf("Stein的结果：\n"); 
begin3=clock();
 for(i=0;i<10;i++)
 {	
	m=c[i];n=d[i];
   	t1=Stein(m,n); 
	printf("第%d组的最大公约数是 %d",i+1,t1);    /*最大公约数*/
	printf("\n");
}
	end3=clock();
	cost3 = (double)(end3 - begin3)/CLOCKS_PER_SEC;
   

printf("穷举法的结果：\n");
begin4=clock();
   for(i=0;i<10;i++)
 {	
	m=c[i];n=d[i];
   	t1=divisor(m,n); 
	printf("第%d组的最大公约数是 %d",i+1,t1);    /*最大公约数*/
	printf("\n");
}
end4=clock();
cost4 = (double)(end4 - begin4)/CLOCKS_PER_SEC;
    printf("辗转相除法的 time cost is: %lf secs\n",cost1);
    printf("更相减损的 time cost is: %lf secs\n", cost2);
    printf("Stein方法的 time cost is: %lf secs\n",  cost3);
    printf("穷举法的time cost is: %lf secs\n", cost4);
}

四：四种算法的比较
这是输入十组3位整数的算法时间

这是输入十组4位整数的算法时间

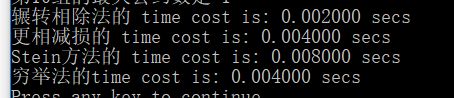
这是输入二十组3位整数的算法时间

这是输入二十组4位整数的算法时间

通过对算法时间的比较，我们可以得出一个初步的结论，当输入的数据规模较小时，辗转相除法所用的时间较少，Stein算法所用时间较多；当数据规模较大时， Stein算法所用时间较少，而辗转相除法所用的时间较多；所以我们应该根据数据规模的大小选择适当的算法；