二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

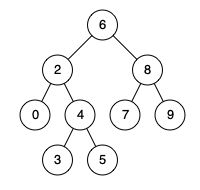
例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

• 示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

• 示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

• 说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

• 分析

搜索二叉树的特点：左子节点的值小于父节点，右子节点的值大于父节点，我们要找的节点之前的所有结点一定同时大于或小于函数输入中的两个节点的之，也就是说找到第一个不能同时大于或小于两个节点的值的那一个节点，就是我们要找的那个节点。

• code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        TreeNode *res = root;
        while(res->val != p->val && res->val != q->val) {
            if (res->val > p->val && res->val > q->val) {
                res = res->left;
            } else if (res->val < p->val && res->val < q->val) {
                res = res->right;
            } else {
                break;
            }
        }
        return res;
    }
};