图论-网络流⑦-费用流解题

图论-网络流⑦-费用流解题

上一篇：图论-网络流⑥-费用流

下一篇：图论-网络流⑧-有上下界的网络流

参考文献：

https://www.luogu.com.cn/blog/user9012/solution-p3980

大纲

• 什么是网络流
• 最大流（最小割）

• $Dinic$ （常用）
• $EK$
• $Sap$
• $Ford-Fulkerson$（不讲）
• $HLPP$ （快）

• 最大流解题
• 费用流

• $EK$ 费用流
• $Dinic$ 费用流
• $zkw$ 费用流

• 费用流解题 $\text{Start}$ $\text{End}$

• 有上下界的网络流

• 无源汇上下界可行流
• 有源汇上下界可行流
• 有源汇上下界最大流
• 有源汇上下界最小流
• 最大权闭合子图

• 有上下界的网络流解题

前文中讲了费用流的定义和 $3$ 种费用流算法，这一篇中会讲几道费用流的经典例题。

费用流解题

费用流的解题套路和最大流差不多，无非就是多加了个费用条件。因为费用流的算法时间复杂度很玄学，所以有些时候优化很重要。

[HAOI2010]订货

普通的费用流题目，只需要按图索骥即可。

---

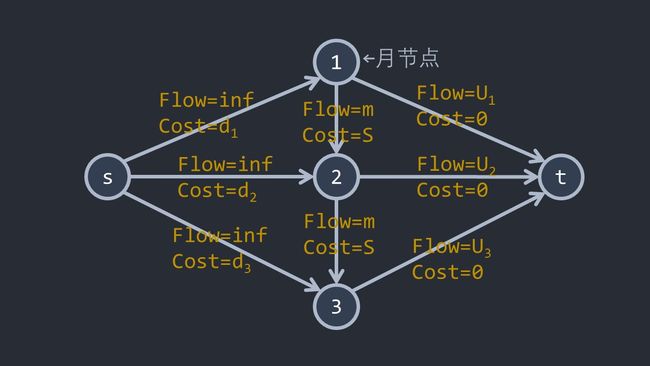
同最大流解题思路，源点表示发货商，汇点表示该公司的客户。每个月都可以买无穷产品，所以 $s$ 向每个月节点连流量为 $\infty$ 费用为 $d_i$ 的边；每个月节点向 $t$ 连流量为 $U_i$ 的边（满足最大流就相当于满足客户），因为每个月还可以储存，所以每个月节点向下个月节点（如果有下个月节点）连流量为 $S$ 费用为 $m$ 的边。 跑个最小费用最大流，总费用就是最低成本。

整理一下：

$Dinic$费用流代码（以前写的，码风很蒻）：

#include 
using namespace std;
const int N=1e6+10;
const int M=6e6+10;
const int inf=1e8+10;
int n,m,S,s,t,fans,cosans;
struct edge{
	int adj,nex,fw,r;
}e[M];
int g[N],top=1;
void add(int x,int y,int z,int w){
	e[++top]=(edge){y,g[x],z,w};
	g[x]=top;
}
int dep[N],cur[N];
bool vis[N];
queue<int> Q;
bool spfa(){
	// puts("spfa()");
	for(int i=1;i<=n;i++)
		vis[i]=0,dep[i]=inf;
	Q.push(s),vis[s]=1,dep[s]=0;
	for(int i=1;i<=n;cur[i]=g[i],i++);
	while(Q.size()){
		int x=Q.front(); Q.pop();
		vis[x]=0;
		for(int i=g[x];i;i=e[i].nex){
			int to=e[i].adj,d=e[i].r;
			if(e[i].fw&&dep[to]>dep[x]+d){
				dep[to]=dep[x]+d;
				if(!vis[to]){
					vis[to]=1;
					Q.push(to);
				}
			}
		}
	}
	return dep[t]!=inf;
}
int dfs(int x,int F){
	// puts("dfs");
	if(!F||x==t)
		return F;
	int flow=0,f;
	vis[x]=1;
	for(int i=cur[x];i;i=e[i].nex){
		int to=e[i].adj; cur[x]=i;
		if(!vis[to]&&dep[x]+e[i].r==dep[to]&&
		(f=dfs(to,min(F,e[i].fw)))>0){
			e[i].fw-=f;
			e[i^1].fw+=f;
			flow+=f,F-=f;
			if(!F){
				vis[x]=0;
				break;
			} 
		}
	}
	return flow;
}
int main(){
	scanf("%d%d%d",&n,&m,&S);
	for(int i=1,x;i<=n;i++){
		scanf("%d",&x);
		add(i+1,n+2,x,0);
		add(n+2,i+1,0,0);
	}
	for(int i=1,x;i<=n;i++){
		scanf("%d",&x);
		add(1,i+1,inf,x);
		add(i+1,1,0,-x);
	}
	for(int i=1;i<n;i++)
		add(i+1,i+2,S,m),
		add(i+2,i+1,0,-m);
	s=1; n=t=n+2;
	while(spfa()){
		int d=dfs(s,inf);
		fans+=d,cosans+=d*dep[t];
	}
	printf("%d\n",cosans);
	return 0;
}

总结：普通费用流题按图索骥即可。

[SDOI2010]星际竞速

思维难度排名前 $10\%$，蒟蒻以前写的题解：传送门

---

我把这题的思想叫做接力棒思想，因为我就是想到接力棒的时候突然知道怎么做的。这题你想一个流遍历所有点是不可能的，因为这道题正好否决了所以这样的方法。

正解就像在接力跑。想象有 $n+1$ 个人接力跑 ，刚开始时都在 $s$ 点上，分别对应 $s$ 和 $1\sim n$ 这 $n+1$ 个节点，开始时接力棒在 $s$ 那个人手上。
$1\sim n$ 算操场里的点，开始时 $s$ 对应的运动员开跑。在未经召唤的情况下从场外到场内节点 $i$ 需要花费 $a_i$，所以 $s$ 运动员就花费某个 $a_x$ 到场内节点 $x$，然后到达节点后打卡，休息。
然后 $x$ 节点对应的运动员受到 $s$ 的召唤，免费瞬移到 $x$ 节点，然后沿着道路花费相应的费用到另一个节点，并打卡，休息，召唤该节点对应的运动员。
然后反复这个过程，除了 $s$ 节点对应的运动员，别的运动员也可以花费 $a_i$ 的费用跑到场内，或免费受召唤瞬移，最终所有 $1\sim n$ 节点被打卡一次后，接力赛结束。
然后按照被转化的问题，按图索骥一下建个图，最后的最大流最小费用就是答案。

整理一下：

注1：这个图表示样例 $1$ 的连边方法。
注2：题目中说只能星际航行到引力大的星球。
注3：图中的边流量都为 $1$。

$\text{AC}$ 代码：

#include 
using namespace std;
const int N=2e3+10;
const int M=2e6+10;
const int inf=1e8;
int d(){int x; scanf("%d",&x); return x;}
int n,m,p,s,t,a[N],fans,cans;
struct edge{
	int adj,nex,fw,r;
}e[M];
int g[N],top=1;
void add(int x,int y,int z,int w){
	e[++top]=(edge){y,g[x],z,w};
	g[x]=top;
}
void Add(int x,int y,int z,int w){
	// printf("%d-%d %d %d\n",x,y,z,w);
	add(x,y,z,w),add(y,x,0,-w);
}
int dep[N],cur[N];
bool vis[N];
queue<int> Q;
bool spfa(){
	for(int i=1;i<=p;i++)
		vis[i]=0,dep[i]=inf,cur[i]=g[i];
	Q.push(s),vis[s]=1,dep[s]=0;
	while(Q.size()){
		int x=Q.front(); Q.pop();
		vis[x]=0;
		for(int i=g[x];i;i=e[i].nex){
			int to=e[i].adj,d=e[i].r;
			if(e[i].fw&&dep[to]>dep[x]+d){
				dep[to]=dep[x]+d;
				if(!vis[to]){
					vis[to]=1;
					Q.push(to);
				}
			}
		}
	}
	return dep[t]!=inf;
}
int dfs(int x,int F){
	if(!F||x==t)
		return F;
	int flow=0,f;
	vis[x]=1;
	for(int i=cur[x];i;i=e[i].nex){
		int to=e[i].adj; cur[x]=i;
		if(!vis[to]&&dep[x]+e[i].r==dep[to]&&
		(f=dfs(to,min(F,e[i].fw)))>0){
			e[i].fw-=f;
			e[i^1].fw+=f;
			flow+=f,F-=f;
			if(!F){
				vis[x]=0;
				break;
			} 
		}
	}
	return flow;
}
int main(){
	n=d(),m=d(),p=t=2*n+2,s=t-1;
	for(int i=1,x;i<=n;i++){
		a[i]=d(); Add(i+n,t,1,0);
		Add(s,i,1,0),Add(s,i+n,1,a[i]);
	}
	for(int i=1;i<=m;i++){
		int x=d(),y=d(),z=d();
		if(x>y) swap(x,y);
		if(z<a[y]) Add(x,y+n,1,z);
	}
	while(spfa()){
		int D=dfs(s,inf);
		fans+=D,cans+=D*dep[t];
	}
	printf("%d\n",cans);
	return 0;
}

总结：网络流题一定、一定、一定要多思考。

[NOI2008]志愿者招募

本蒟蒻做过的最巧妙的费用流题目（没有之一），很谔谔。

---

源点连志愿者，志愿者连控制的天（区间），天连汇点是最典型的爆〇方式。这题的思想有点像有些比较抠的差分约束题的思想但又不是。

正解就像在闯关。每一天就是一关，开始时你有 $\infty$ 个小人，到第 $n+1$ 关时还有这么多小人，就赢了。 第 $i$ 天只能免费通过 $\infty -a_i$ （注：这里的 $\infty$ 是有数值的，$\infty \ne \infty -a_i$）个人，剩下的人需要乘坐不免费的时空穿越机。
每个志愿者就是一台能从 $s_i$ 关跳到 $t_i+1$ 关的时空穿越机，花费为 $c_i$，只能乘坐一个小人。 但因为每种志愿者有无限个，所以可以看作能乘坐无穷小人，费用为 $c_i/$人。
求最后赢得所有 $n+1$ 关最少的费用。然后按图索骥建个图，跑个最大流最小费用就是答案。

整理一下：

注：图为题目样例。

$\text{AC}$ 代码：

#include 
using namespace std;
const int N=1e3+10;
const int M=1e4+10;
const int P=2e4+10;
const int E=3e7+10;
const int inf=1e8;
int d(){int x;scanf("%d",&x);return x;}
int n,m,p,s,t,fans,cans;
struct edge{
	int adj,nex,fw,r;
}e[E];
int g[P],top=1;
void add(int x,int y,int w,int r){
	e[++top]=(edge){y,g[x],w,r};
	g[x]=top;
}
void Add(int x,int y,int w,int r){
	add(x,y,w,r),add(y,x,0,-r);
}
int dep[P],cur[P];
bool vis[P];
queue<int> q;
bool spfa(){
	for(int i=1;i<=p;i++)
		vis[i]=0,dep[i]=inf,cur[i]=g[i];
	q.push(s),vis[s]=1,dep[s]=0;
	while(q.size()){
		int x=q.front();q.pop(),vis[x]=0;
		for(int i=g[x];i;i=e[i].nex){
			int to=e[i].adj,d=e[i].r;
			if(e[i].fw&&dep[to]>dep[x]+d){
				dep[to]=dep[x]+d;
				if(!vis[to]) vis[to]=1,q.push(to);
			}
		}
	}
	return dep[t]!=inf;
}
int dfs(int x,int F){
	if(!F||x==t)
		return F;
	int flow=0,f;
	vis[x]=1;
	for(int i=cur[x];i;i=e[i].nex){
		int to=e[i].adj; cur[x]=i;
		if(!vis[to]&&dep[x]+e[i].r==dep[to]
		&&(f=dfs(to,min(F,e[i].fw)))>0){
			e[i].fw-=f,e[i^1].fw+=f;
			flow+=f,F-=f;
			if(!F){vis[x]=0; break;}
		}
	}
	return flow;
}
int main(){
	n=d(),m=d();
	p=t=n+m+3,s=t-1;
	for(int i=1;i<=n;i++)
		Add(i,i+1,inf-d(),0);
	for(int i=1;i<=m;i++){
		int S=d(),T=d(),C=d();
		Add(S,T+1,inf,C);
	}
	Add(s,1,inf,0),Add(n+1,t,inf,0);
	while(spfa()){
		int D=dfs(s,inf);
		fans+=D;
		cans+=dep[t]*D;
	}
	printf("%d\n",cans);
}

总结：有什么好总结的呢，脑洞和思考最重要吧。

下一篇会讲有关有上下界的网络流的知识。

祝大家学习愉快！